從一個題淺談一類不等式題的解題策略
浙江省余姚市第八中學 陳銀燕
高考命題重點考查均值不等式和證明不等式的常用方法,單純不等式的命題,主要出現在選擇題或填空題,一般難度不太大。在近年的高考中,不等式的考查有選擇題、填空題、解答題,不僅考查不等式的基礎知識、基本技能、基本方法,而且還考查了分析問題、解決問題的能力。解答題以函數、不等式、數列、導數相交匯處命題,函數與不等式相結合的題多以導數的處理方式解答,函數不等式相結合的題目,多是先以直覺思維方式定方向,以遞推、數學歸納法等方法解決,具有一定的靈活性。在一次聯考中,填空題最后一題考查基本不等式。下面就由此題展開,談談對于此類不等式的解題策略和思考。
一、考題引入,一題多解
初次看到這一題,腦海中的第一種想法是利用基本不等式。在考試之前,正好在帶領學生復習不等式的知識,只是學生中能靈活運用基本不等式的不多,只能解常見題,簡單不等式求最值,有個別學生連“一正,二定,三相等”都不能很好理解。以下是對這個題的幾種不同解法。
∵ S=xy,x>0,y>0,∴ S>0,
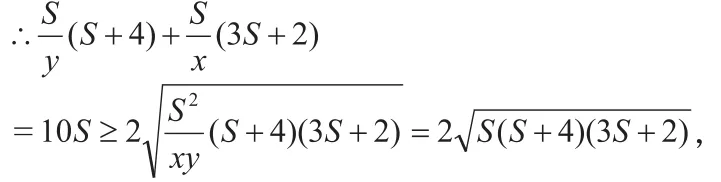
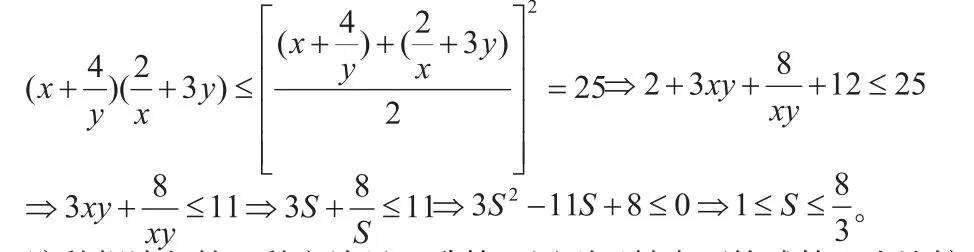
這種想法與第一種方法是一致的,用到了基本不等式的一個比較常用的變形可以很好地把兩個數的加法與乘法聯系在一起。
其實這題是泰州2015屆高三調研(三)卷中14題原題,除了上面兩種想法外,還可以用其他的方法進行拆分組合,最大最小值分開來算。(因為此題涉及的是正實數x,y,以下解題不具體說明)
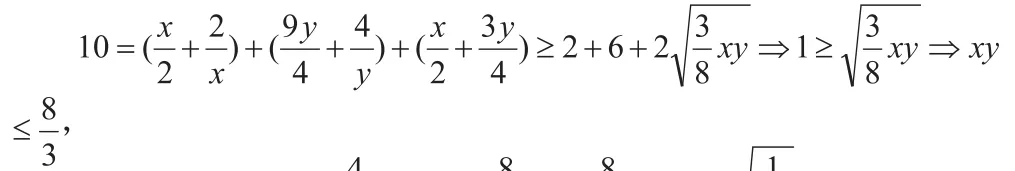
對學生來說,解法三、四很難會想到,解法四對學生不作要求,解法五的想法比較靈活,用函數的思想解決最值問題,前提先消元,視為x的函數,用函數性質來解題。
上述是一題多解,從不同角度來解決不等式求最值問題,這類題比較喜歡放在填空題壓軸題的位置,在高考中出現概率非常高,變式題也非常多。
二、考題鏈接,變式拓展
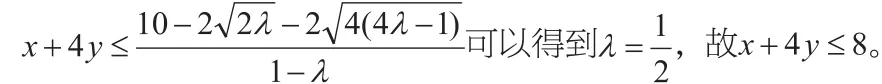
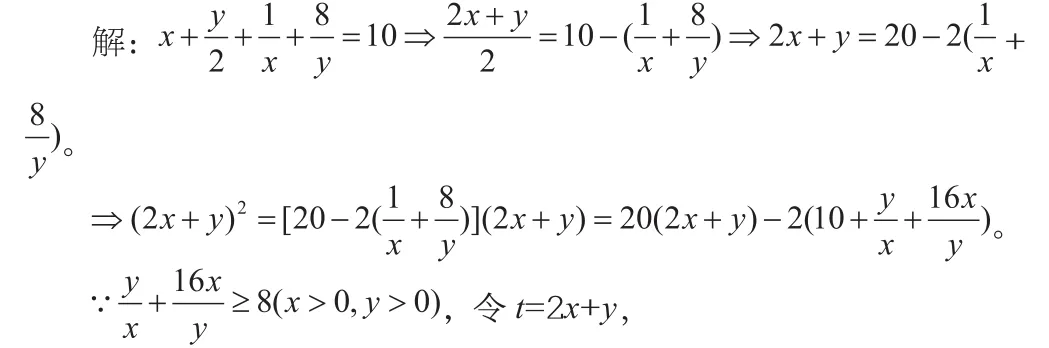
∴t2≤20t-362≤t≤18,當且僅當x=3,y=12時,(2x+y)max=18。
變式三的這種解法是比較典型的,出現2x+y這個整體,用整體的想法,也可以對原題左右同乘2x+y,利用基本不等式把其變為定值。實際上,大多數題目是湊好的,否則在用基本不等式的時候,不等式右邊是無理數,題目再做下去就比較麻煩,當然個別題除外(比如可湊成完全平方解答)。
另解:這個題也可以構造“1”,關鍵是怎么構造。
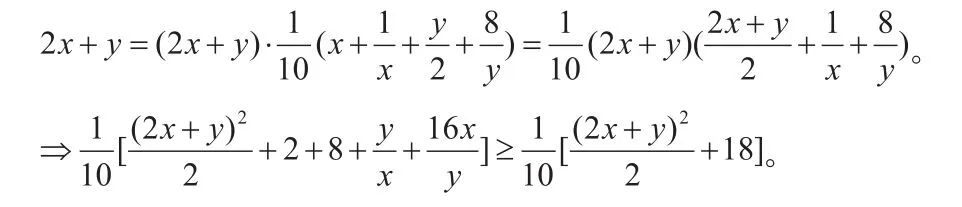
掌握這兩種方法,解溫州市2015屆高三第一次適應性測試數學第6題,已知正數x,y滿足則求x+y的最大值就非常方便了。
以上是對這一類不等式提供的幾種解題策略,但具體問題還需具體分析。在復習解不等式過程中,注意培養、強化與提高函數與方程、等價轉化、分類討論、數形結合的數學思想和方法,逐步提升數學素養,提高分析解決綜合問題的能力。能根據各類不等式的特點,變形的特殊性,歸納出各類不等式的解法和思路以及具體解法。

