問渠哪得清如許 “唯”有源頭活水來
江蘇省盱眙中學 李修峰
課本是數學知識和數學思想方法的載體,又是高考命題者的源泉,更是我們平時教學的依據。部分高考試題是以課本題為原型進行變化或延伸命制得來的,所以在高三復習教學時,我們要多注重課本例習題的示范作用,并在此基礎上進行變式和拓寬,提高課堂教學效益的最大化。
一、課本題
蘇教版《普通高中課程標準試驗教科書·數學·必修五》第24頁第6題:如圖,已知∠A為定角,P、Q分別在∠A的兩邊上,PQ為定長,當P、Q處于什么位置時,△APQ的面積最大?

當∠P=∠Q,即AP=AQ時等號成立,△APQ的面積最大。
解法二:在△APQ中,由余弦定理PQ2=AP2+AQ2-2AP·AQcosA≥2AP·AQ-2AP·AQcosA得
當且僅當AP=AQ時等號成立,即△APQ的面積最大。
解法三:以PQ所在的直線為x軸,以PQ中垂線所在的直線為y軸,建立如圖所示的平面直角坐標系,設A(x,y),則

二、試題拓展
三、方法拓展

即S△ABC取到最大值。
解法二:以AB所在直線為x軸,以AB中垂線為y軸建立如圖所示的平面直角坐標系,設C(x,y),則A(-1,0),B(1,0),由得

化簡得(x-3)2+y2=8,故點C的軌跡為以(3,0)為圓心,以為半徑的圓(與x軸交點坐標除外),
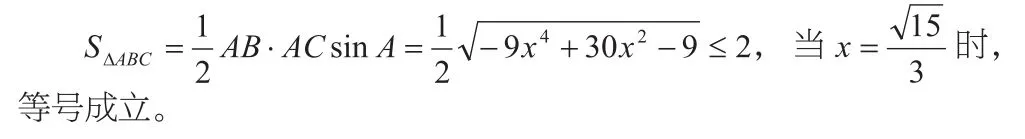
解法二:如圖,以BC所在的直線為x軸,以線段BC的中垂線為y軸建立平面直角坐標系,設A(0,a),B(-b,0),C(b,0),則

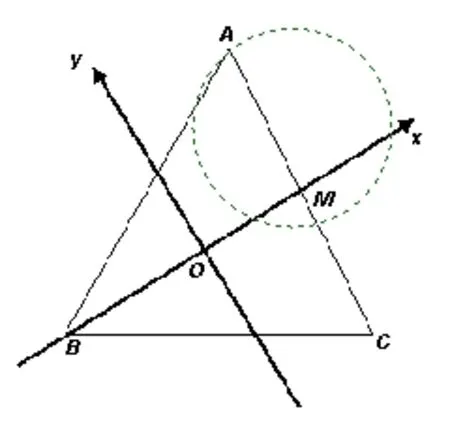
解法三:如圖,以BM所在的直線為y軸,以BM的中垂線所在的直線為x軸建立平面直角坐標系,設
高考試題大多來源于課本,在數學教學中經常將課本中的例題和習題在解題方法思想上進行挖掘進行變式探究,可引導學生從多角度、多方位思考問題,深入理解概念本質,靈活運用定理公式,既豐富了教學內容,又培養了學生思考、探究問題的能力,從而能大大提高教學效率。

