提煉基本模型，促進能力提升

☉江蘇省如東縣茗海初級中學陳興國

以教材中的例題、習題作背景并進行中考試題的命制是最為普遍的，這些由命題專家巧妙構思編擬的中考試題往往具有權威性與導向性，教師在具體教學中應著眼于基本幾何模型的提煉，并因此幫助學生提升學習效率與創造能力.

一、試題呈現

題目：如圖1，正方形ABCD的邊長是3cm，P、Q分別從B、A出發沿BC、AD方向運動，P、Q兩點的運動速度分別為1cm/秒、2cm/秒.連接AP，并過點Q作QE⊥AP，垂足為E.

（1）求證：△ABP∽△QEA；

（2）若運動時間為t，則t等于何值時，△ABP≌△QEA？

（3）設△QEA的面積為y，如何用運動時間t來表示△QEA的面積y呢？（不考慮t的取值范圍）

（提示：（2）、（3）兩問的解答可以不分先后）

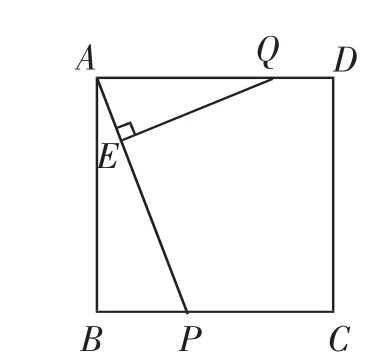
圖1

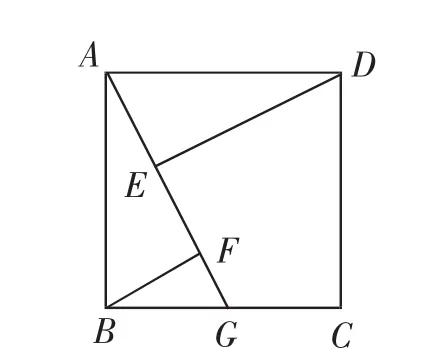
圖2

這道梯度清晰的中考試題能很好地考查學生對三角形全等、相似及函數有關知識的掌握情況.事實上，這是一道根據課本原題變化而來的新題，原題為：如圖2，四邊形ABCD為正方形，點G是BC邊的中點，DE⊥AG，BF∥DE交AG于F，求證：AF－BF=EF.

將原題中的“BF∥DE交AG于F”去掉就變成了上述中考試題.

二、基本圖形與模型的探索

從上述課本原題與中考試題的觀察中，不難看出其中所蘊含的基本圖形與幾何模型：如圖3，在正方形ABCD中，點E、F分別在BC、CD上，AE、BF交于點O.

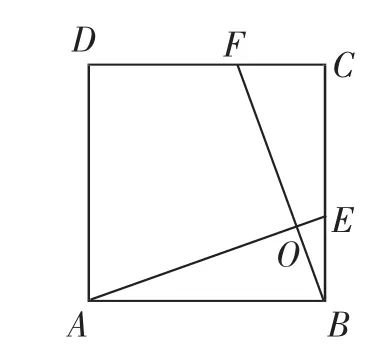
圖3

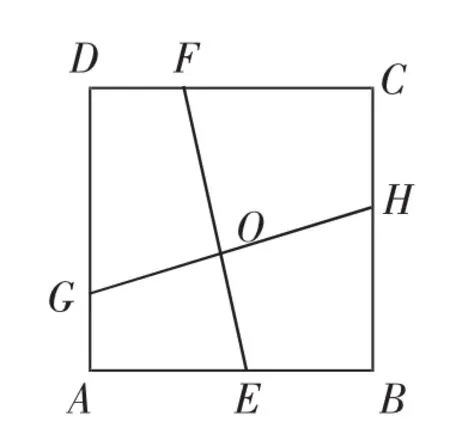
圖4

性質1：若AE⊥BF，則AE=BF（或BE=CF）.

性質2：若AE=BF（或BE=CF），則AE⊥BF.

性質3：若點O是中心對稱圖形的對稱中心，且存在AE⊥BF，則該圖形的面積被AE、BF分成了四等份.

如果把線段AE、BF分別平移至GH、EF處（如圖4），結論EF=GH仍成立.

直角與互余的性質得到了很好的利用，由此也不難看出如果由正方形變成矩形會存在三角形相似與對應線段成比例的結論.

如圖5，在矩形ABCD中，點E、F分別在AB、AD上，且DE⊥CF，則

若把線段DE、CF分別平移至NM、HQ處（如圖6），結論仍成立.

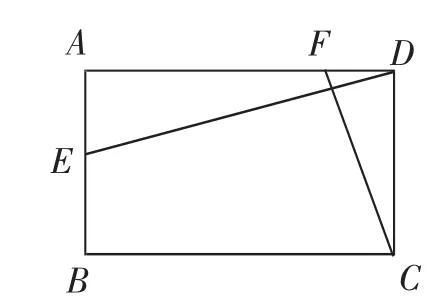
圖5

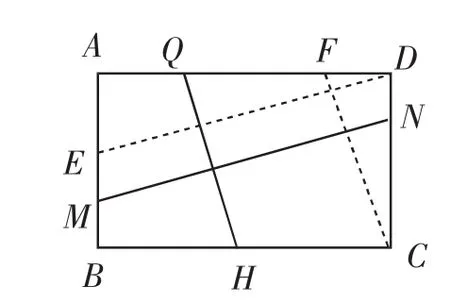
圖6

上述圖形中可提煉的模型如下：

模型1：正方形+線段垂直或相等=線段相等或垂直.

模型2：中心對稱圖形+線段垂直或面積四等分=面積四等分或線段垂直.

模型3：矩形+線段垂直或線段成比例=線段成比例或線段垂直.

三、利用模型解題以促學生能力提升

1.利用模型1解題

例1已知：如圖7，在正方形ABCD中，點E在邊CD上，AQ⊥BE于點Q，DP⊥AQ于點P.

（1）求證：AP=BQ；

（2）請在不添加任何輔助線的情況下直接寫出圖中四對線段，令各對中較長線段和較短線段長度之差與PQ的長度相等.

分析：由模型1可得AQ=DP，則可證明圖形全等并得出AP=BQ，根據全等形可得AQ-BQ=PQ或PD-AP=PQ.

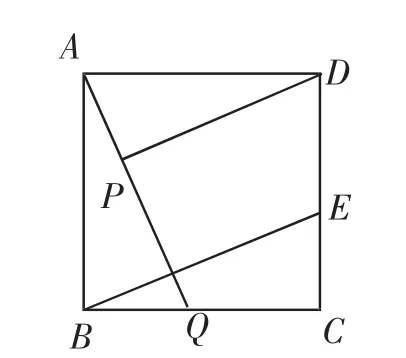
圖7

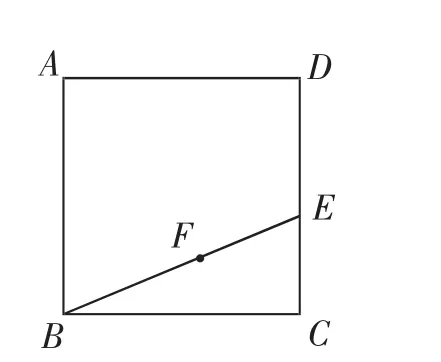
圖8

例2如圖8，正方形ABCD的面積為3cm2，E為BC邊上一點，∠BAE=30°，F為AE的中點，過點F作直線分別與AB、DC交于M、N兩點，若MN=AE，則AM的長為_____cm.

分析：由模型2可得MN⊥AE，由勾股定理與∠BAE=30°可求出AE=2，則AF=1，因此AM

2.利用模型2解題

例3【問題探究】

（1）在圖9中作兩條直線并將圓的面積四等分.

（2）如圖10，M為正方形ABCD內一定點，在圖9中作兩條直線，并將正方形ABCD的面積四等分，請說明你的理由.

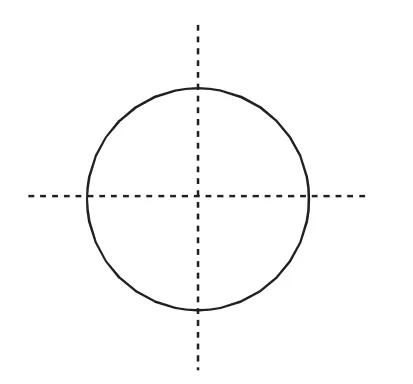
圖9

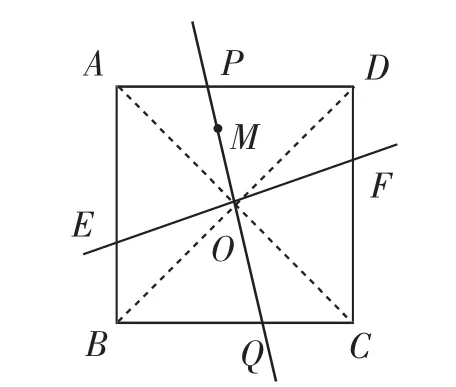
圖10

【問題解決】

（3）如圖11，在四邊形ABCD中，AB∥CD，AB+CD=BC，點P為AD的中點.若AB=a，CD=b，且b＞a，BC邊上是否存在一點Q，令PQ所在直線將四邊形ABCD的面積兩等分呢？若有，PQ的長為多少？若沒有，理由何在？

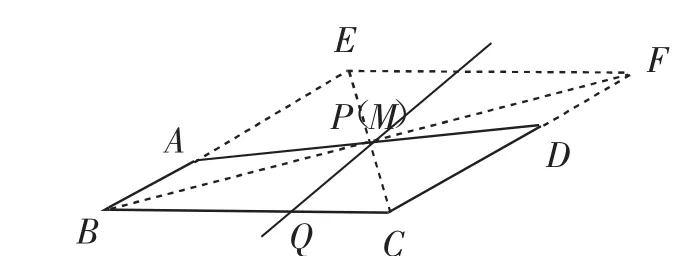
圖11

分析：（1）由模型2可知，作兩條經過圓心且相互垂直的直線即可令問題得解.

（2）聯想模型2，過點M與正方形ABCD對角線的交點O作直線OM并和AD、BC相交于點P、Q，過點O作OM的垂線，并與AB、CD相交于E、F，則直線OM將正方形ABCD的面積四等分，如圖10.

（3）如圖11，延長BA至點E，使AE=b，延長CD至點F，使DF=a，連接EF.

由BC∥CF，BC=BE=CF=a+b，可證四邊形BCFE為菱形，連接BF交AD于點M，則△MAB≌△MDF，則AM=DM，則點M與P重合，則點P為菱形BCEF的對角線的交點.

在BC上截取BQ=CD=b，則CQ=AB=a.設P點至菱形BCFE一邊的距離為d，則

所以，當BQ=b時，直線PQ將四邊形ABCD的面積分成了兩等份.

3.利用模型3解題

例4【探究證明】

（1）班上學習小組在討論矩形內兩條相互垂直的線段和矩形兩鄰邊的數量關系時給出了以下問題，請證明.

如圖12，矩形ABCD中，EF⊥GH，EF分別與AB、CD交于點E、F，GH分別與AD、BC相交于點G、H.求證

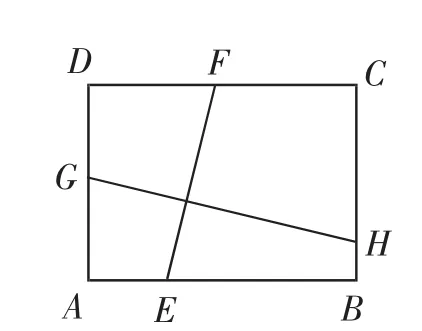
圖12

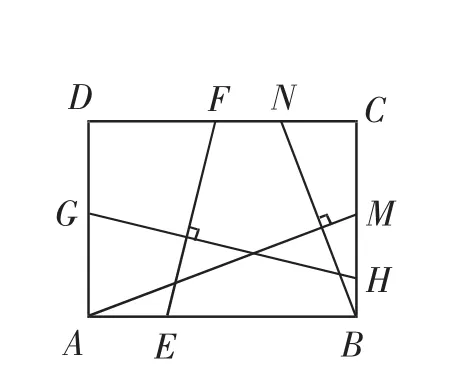
圖13

【結論應用】

（2）如圖13，在滿足（1）的條件下，有AM⊥BN，點M、N分別在BC、CD邊上的值為______.

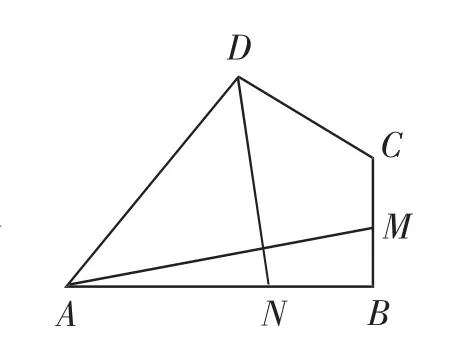
圖14

【聯系拓展】

（3）如圖14，四邊形ABCD中，∠ABC=90°，AB=AD=10，BC=CD=5，AM⊥DN，點M、N分別在BC、AB邊上，則的值為______.

分析：（1）由模型3，過點A作AP∥EF交CD于P，過點B作BQ∥GH交AD于Q，如圖15，易證AP=EF，GH=BQ，△PDA∽△QAB，由相似三角形的性質解題.

（3）過點D作平行于AB的直線，與過點A且平行于BC的直線交于點R，與BC的延長線交于點S，如圖16，可證四邊形ABSR為矩形，由模型3可得

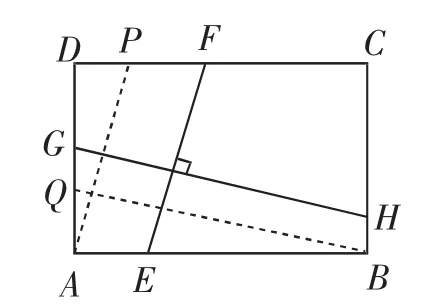
圖15

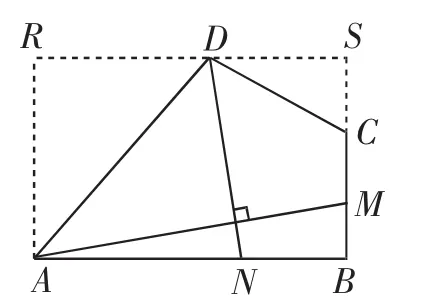
圖16

設SC=x，DS=y，則AR=BS=5+x，RD=10－y.

在Rt△CSD中，結合勾股定理，可得：

在Rt△ARD中，結合勾股定理，可得：（5+x）2+（10－y）2=100. ②由①和②，可求得x，并得出AR，問題得解.

四、反思

1.研究、開發教材需加強

很多中考試題都是專家在教材例題、習題的研習上精心開發、構思而編寫出的，教師應能看到其中思路變化上的類比遷移并進行適當的拓展探索，改編一些例題中的原題并將題中豐富的教學價值體現出來，使學生能夠在此類題的變化與探索中掌握、遷移其中的思路、方法與技能，使教材和中考試題之間的聯系變得更加緊密.

2.建模教學需加強

幾何圖形中的每個基本圖形都可以看作幾何模型，幾何模型所具備的性質和研究方法對很多復雜的幾何問題都具備重要的作用和意義，教師應加強對基本模型的研究，并培養學生增強探尋基本模型的能力，使學生能夠逐步獲得利用模型解題的思維方法與能力，并積累一定的解題經驗.

3.推理能力需強化

對幾何圖形性質的探究在近年中考試題中體現得尤為明顯，學生在幾何問題上的思維方式與水平在幾何問題的解決中也彰顯無余，因此，教師在平時的教學中，應有意識、有目的地變化問題的條件與結論，引導學生在圖形的結構重組和更新中對題目的條件、結論進行大膽嘗試與聯想，打開思維的大門，并順利建立模型，以發展猜想與創新能力.W