強(qiáng)化數(shù)學(xué)思想方法，提升幾何探究能力

（福建省上杭縣舊縣中學(xué) 福建上杭 364214）

中考試題凝聚著命題專家的智慧，在復(fù)習(xí)階段適當(dāng)選用或者改編中考試題，讓學(xué)生在探究活動(dòng)中體驗(yàn)圖形變化、幾何直觀、特殊化與一般化、分類討論、化歸等幾何探究的基本思想方法，并在總結(jié)反思中提煉，在遷移訓(xùn)練中自覺運(yùn)用，能提高復(fù)習(xí)效率，也有助于豐富數(shù)學(xué)思想方法，提升學(xué)生的幾何探究能力。 下面筆者以一道中考數(shù)學(xué)壓軸題為例，談?wù)勥@方面的體會(huì)。

題目：在正方形ABCD中，對(duì)角線AC、BD交于點(diǎn)O，點(diǎn)P在線段BC上（不含點(diǎn)B），

（1）當(dāng)點(diǎn)P與點(diǎn)C重合時(shí)（如圖1）.求證：△BOG≌△POE；

（3）把正方形ABCD改為菱形，其他條件不變（如圖3），若∠ACB = α，求的值（用含α的式子表示）.

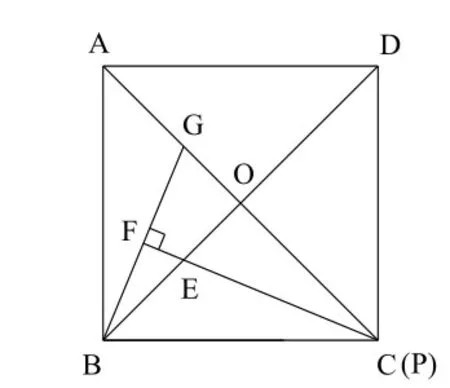
圖1

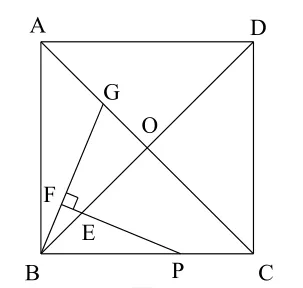
圖2

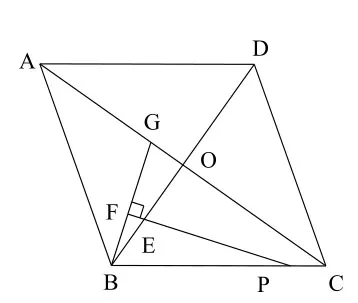
圖3

一、改編試題

如圖2，在正方形ABCD中，對(duì)角線AC、BD交于點(diǎn)O，點(diǎn)P在線段BC上（不含點(diǎn)B），PE交BO于點(diǎn)E，過點(diǎn)B作BF⊥PE，垂足為F，交A C于點(diǎn)G.試探究：的值，證明你的結(jié)論，并將命題進(jìn)行推廣。

設(shè)計(jì)意圖：近年來，不少中考試題的設(shè)計(jì)都從特殊情況開始探究，再進(jìn)一步拓展到一般情況；或是先限定在某一范圍內(nèi)探究結(jié)論成立的情況，再拓展到其他范圍，進(jìn)一步判斷其結(jié)論是否也成立.其用意在于考查學(xué)生對(duì)特殊到一般思想方法的理解和運(yùn)用水平以及對(duì)于數(shù)學(xué)拓展研究的能力.然而這種思想方法已經(jīng)被命題者用來設(shè)計(jì)問題了，學(xué)生只需按照命題者的要求，解答一個(gè)個(gè)小問題就可以，與命題者的初衷相去甚遠(yuǎn)。

二、解法探究

1.審題

（1）仔細(xì)閱讀題目，并在圖形上標(biāo)注已知條件和能簡(jiǎn)單得到的結(jié)果，如圖4；

（2）認(rèn)真觀察圖形，尋找圖形特征并分離出基本圖形△BCG.

2.猜想

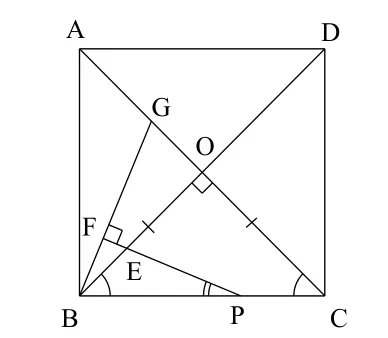
圖4

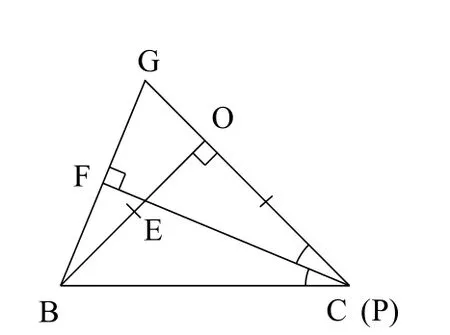
圖5

（2）特殊化：讓點(diǎn)P與點(diǎn)C重合，如圖5 ，此時(shí)△BPG為等腰三角形，同時(shí)Rt△BOG≌Rt△POE，∴BG = PE，從而

3.證明思路

思路1：尋找特殊情形的本質(zhì)特征

圖5的特征在于等腰三角形中含有全等三角形，據(jù)此在圖4中過點(diǎn)P作PM // AC交BG于M，交BO于N，如圖6，這樣構(gòu)造出與圖5類似的圖形△BPM.

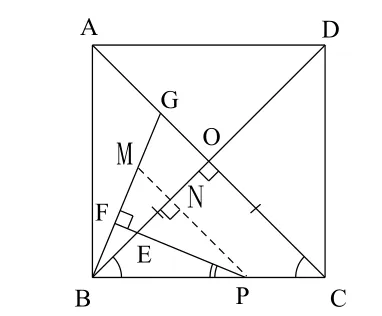
圖6

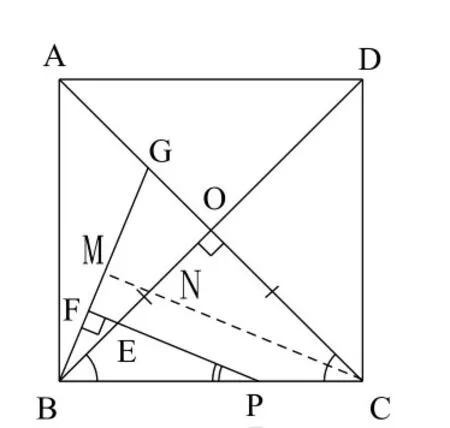
圖7

思路2：尋找一般情形與特殊情形之間的聯(lián)系

比較圖4與圖5，圖4中仍有等腰△BPG，為構(gòu)造出特殊情形的圖形，可過C作CM // EP交BG于M，交BO于N。由特殊情形知：而這可由圖7中CM // EP得到，即有得到。

4.拓展

（1）突破某一范圍的條件限制

如去掉“點(diǎn)P在線段BC上（不含點(diǎn)B）”的限制，會(huì)有怎樣的結(jié)果？通過畫圖可知，此時(shí)仍有等腰三角形中含全等三角形的結(jié)構(gòu)，結(jié)論依然成立。從而可推廣為：“點(diǎn)P為線段BC延長(zhǎng)線上一點(diǎn)，其余條件不變時(shí)，結(jié)論仍然成立”，如圖8，證明思路與前面的完全一樣。

（2）改變題目背景

將題目中的條件弱化，如正方形變?yōu)樘厥馄叫兴倪呅?，?jīng)過探究可得：

如圖9，把正方形ABCD改為菱形，其他條件不變，若∠ACB =α，求的值（用含α的式子表示）.

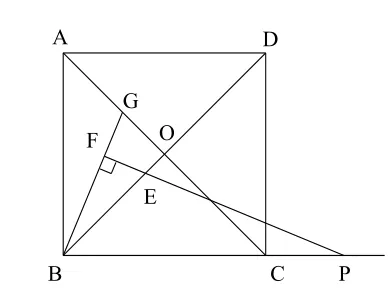
圖8

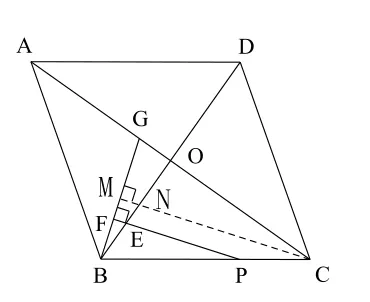
圖9

思路分析:

因?yàn)橥茝V過程中保持了原題的等腰△BCG結(jié)構(gòu)，所以證明的思路也與原來類似。 如過點(diǎn)C作CM // EP交BG于M，交BO于N，由于此時(shí)∠ACB ≠∠CBO，所以△ONC與△BOG也就不全等了，也即≠ ，但BM = BG仍能成立，所以有只要求出就可以了，由Rt△ONC∽R(shí)t△BOG可得而在Rt△BOC中，所以，

還有其它的證明方法嗎？（讓學(xué)生課后再思考）

三、反思總結(jié)

數(shù)學(xué)思想方法是數(shù)學(xué)學(xué)科的精髓，是將數(shù)學(xué)知識(shí)轉(zhuǎn)化為數(shù)學(xué)能力的橋梁。由于數(shù)學(xué)思想方法屬于隱性知識(shí)，是以具體的知識(shí)為載體，因而對(duì)數(shù)學(xué)思想方法的掌握更多地體現(xiàn)在對(duì)解題策略的思考和選擇上。

華羅庚先生說過，解題時(shí)先足夠地退，退到我們最易看清問題的地方，認(rèn)透了，鉆深了，然后再上去.他認(rèn)為這是學(xué)好數(shù)學(xué)的一個(gè)決竅.因此，以特殊問題為起點(diǎn)，抓住數(shù)學(xué)問題的特征（如本題等腰三角形中含全等三角形），通過逐步分析、比較，層層深入，揭示規(guī)律，由此得到證明的基本思路。對(duì)一般化下的問題，可采取“化歸”的辦法：或抓住特殊化時(shí)圖形的本質(zhì)特征，什么變了，什么沒有變，緊緊抓住末變的；或?qū)⒁话慊碌那樾无D(zhuǎn)化為特殊化情形，看兩者之間有何聯(lián)系，由此得到一般化情況下的證明思路（如本題等腰三角形中含相似三角形）.先特殊化，解決特殊情形下的問題，再一般化，尋求一般問題與特殊問題之間的聯(lián)系，將一般問題進(jìn)行化歸，這是初中幾何一種重要的數(shù)學(xué)思想方法。

四、遷移應(yīng)用

1。如圖10，已知點(diǎn)P是Rt△ABC斜邊AB上一動(dòng)點(diǎn)（不與A，B重合），分別過A、B向直線CP作垂線，垂足分別為E、F，Q為斜邊AB的中點(diǎn).當(dāng)點(diǎn)P在線段AB上不與點(diǎn)Q重合時(shí)，試判斷線段QE與QF的數(shù)量關(guān)系，給予證明并對(duì)該命題進(jìn)行推廣。

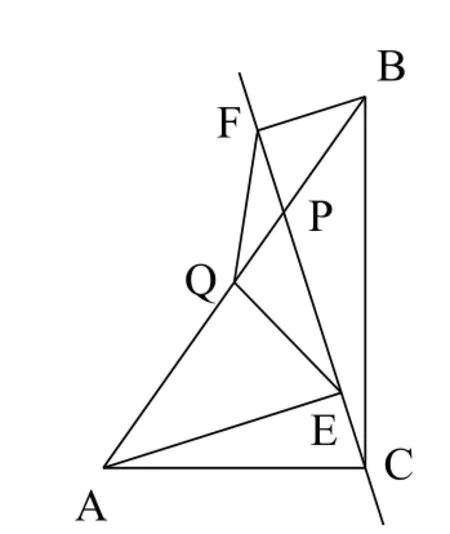
圖10

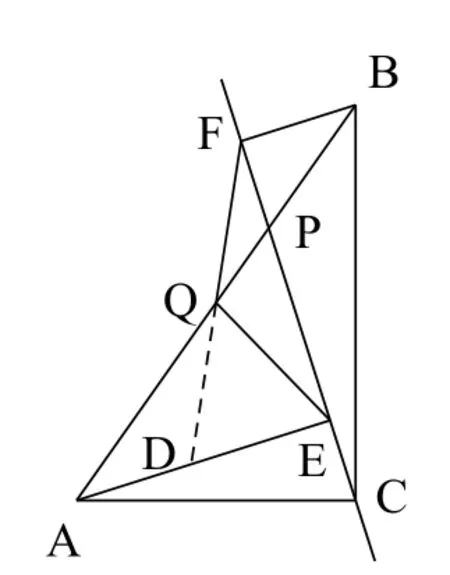
圖11

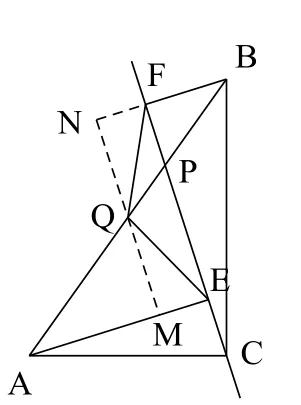
圖12

注：先特殊化，若點(diǎn)P與點(diǎn)Q重合，則由△AQE≌△BQF可得QE = QF。再一般化，受特殊化中利用三角形全等進(jìn)行證明的思路啟發(fā)，延長(zhǎng)FQ交AE于點(diǎn)D，證明△AQD≌△BQF得QD = QF，再根據(jù)Rt△FDE中QE為斜邊FD的中線，得到QE = QF，如圖11；或過點(diǎn)Q作EF的平行線分別交AE、BF于點(diǎn)M、N，證明△AQM≌△BQN得QM = QN，再證△EQM≌△FQN得QE = QF，如圖12。

推廣：當(dāng)點(diǎn)P在線段BA或AB的延長(zhǎng)線上時(shí)，結(jié)論仍然成立。

2.如圖13，在Rt△ABC中，∠C = 90°，D為AB中點(diǎn)，點(diǎn)M、N分別在BC、AC邊上，且DM⊥DN，作MF⊥AB于點(diǎn)F，NE⊥AB于點(diǎn)E.試探究AE和DF的數(shù)量關(guān)系，并加以證明，最后將該命題進(jìn)行推廣。

注：先特殊化，若AC = BC，且DM⊥BC，DN⊥AC，得到圖14，顯然AE = DF。其次一般化，在圖14中先去掉條件DM⊥BC，DN⊥AC，如圖15，再去掉條件AC = BC ，如圖13，此時(shí)AE≠NE，但從圖中可以看出△NED和△MFD也不全等，受基本圖形的啟發(fā)，可得到△NED∽△MFD（全等可看著相似的特殊情況，或作DN′⊥AC，DM′⊥BC，此時(shí)有△DN′N∽△DM′M，如圖15），進(jìn)而有又△NEA∽△MFB，可得再由線段比例關(guān)系的換算可得出結(jié)論。

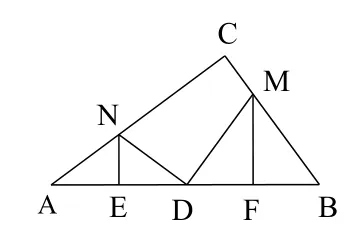
圖13

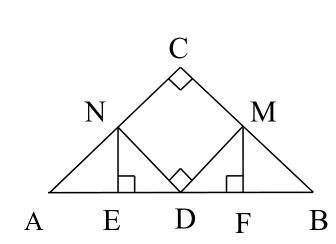
圖14

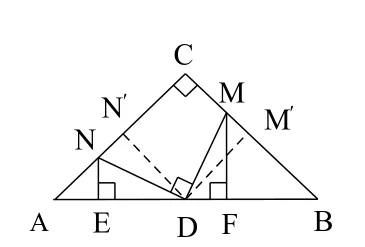
圖15

推廣：若BD = kAD（k為任意正整數(shù)），條件中的“點(diǎn)M在BC上”改為“點(diǎn)M在線段CB的延長(zhǎng)線上”，其它條件不變，則有AE =kDF。

利用上述改編的中考試題，可以讓學(xué)生將不變的數(shù)學(xué)思想方法置身于變化的題目之中，通過類比遷移，強(qiáng)化基本的數(shù)學(xué)思想方法，使學(xué)生學(xué)會(huì)以“不變”應(yīng)“萬變”，真正達(dá)到舉一反三的效果，從而提高幾何探究能力。