電力系統(tǒng)供電負(fù)荷穩(wěn)定性優(yōu)化控制研究

張守艮

（國網(wǎng)安徽省電力有限公司定遠(yuǎn)縣供電公司，滁州 233200）

在電力系統(tǒng)正常運轉(zhuǎn)的過程中負(fù)荷發(fā)生變化的問題經(jīng)常出現(xiàn)，而只要負(fù)荷發(fā)生擾動便必然會造成系統(tǒng)頻率出現(xiàn)偏差。基于這種情況就需要保證在對供電負(fù)荷穩(wěn)定性優(yōu)化控制系統(tǒng)設(shè)計時的科學(xué)性和合理性，通過這樣來使電力系統(tǒng)負(fù)荷頻率的穩(wěn)定性和電能的質(zhì)量得到有效的保障。在對負(fù)荷頻率進(jìn)行控制的過程中主要是為了實現(xiàn)以下兩個效果：第一，在負(fù)荷發(fā)生變化擾動的情況下使電網(wǎng)負(fù)荷頻率不會出現(xiàn)偏差，并且以此來使聯(lián)絡(luò)線的交換功率能夠回歸到最初設(shè)定的數(shù)值；第二，在一些具有不確定性的外部擾動情況和不確定參數(shù)以及不確定的系統(tǒng)模型出現(xiàn)時要保證所設(shè)計出來的控制器具有一定的魯棒性能。

1 供電負(fù)荷穩(wěn)定性優(yōu)化控制系統(tǒng)模型

本研究之中主要考慮的是如圖1之中所示具有非線性特征的供電負(fù)荷穩(wěn)定性優(yōu)化控制系統(tǒng)的原理模型：

圖1 存在非線性特性的供電符合穩(wěn)定性優(yōu)化控制系統(tǒng)

在圖1中，ΔPd所表示的是負(fù)荷擾動情況；Kp所表示的是發(fā)電機的增益情況；Tp所表示的是發(fā)電機時間常數(shù)；TT所表示的是汽輪機時間常數(shù)；TG所表示的是調(diào)速器時間常數(shù)；Δf（t）所表示的是頻率偏差；ΔPG（t）所表示的是汽輪機的輸出變化情況；ΔXG（t）所表示的是調(diào)速器氣門位置的變化情況。由此發(fā)現(xiàn)圖1電力系統(tǒng)主要包括三個部分：一是調(diào)節(jié)閥的動態(tài)：Gg（s）=1/（TGs+1）；二是汽輪機的動態(tài)：Gt（s）=1/（TTs+1）；三是電力系統(tǒng)的動態(tài) ：Gp（s）=Kp/（TPs+1）。

由此可以將系統(tǒng)模型表示如下公式：

由此可導(dǎo)出：

我們可以將LFC問題理解為一個擾動抑制的問題，應(yīng)用反饋u=-K（s）Δf鎮(zhèn)定對象G（s），并且以此來使ΔPd對頻率變化造成的影響被控制在最小的程度。但是由于調(diào)速器死區(qū)或者發(fā)電速率約束以及限幅限速等問題的影響會使系統(tǒng)的性能受到一定的影響，由此便造成了控制器的復(fù)雜程度和控制難度都出現(xiàn)增加。基于這種情況本研究以控制器的設(shè)計方向為切入點，尋求將這些影響因素消除的方法，并且從最大程度上實現(xiàn)簡化結(jié)構(gòu)和計算便捷的效果。

2 線性自抗擾控制

2.1 結(jié)構(gòu)

結(jié)合國內(nèi)外大量學(xué)者總結(jié)出的一些經(jīng)驗我們可以發(fā)現(xiàn)自抗擾控制并不需要了解被控對象以及擾動的完全模型，只需要對對象的相對階和增益加以了解便可以。我們首先假設(shè)被控系統(tǒng)的模型如下所示：

式中，f（y，u，d）所表示的是系統(tǒng)一些未知的動態(tài)和相關(guān)外部擾動的組合，在對自抗擾控制進(jìn)行設(shè)計的過程中假設(shè)具有一定的未知性，在這里我們將其稱之為廣義擾動。

在自抗擾控制的框架之中主要是通過一個ESO來對f（y，u，d）這些未知的廣義擾動進(jìn)行估計。可以將假設(shè)的系統(tǒng)模型寫成

對該模擬系統(tǒng)的全階Luenberger觀測器進(jìn)行設(shè)計如下所示：

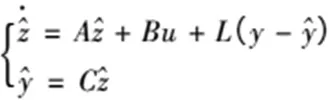
式中，L表示的是觀測器增益：

2.2 參數(shù)整定

通過上述內(nèi)容可以看出一個LADRC需要設(shè)計出兩組的參數(shù)，LESO的觀測器增益LF和r重積分的系統(tǒng)狀態(tài)反饋增益Ko主要是為了調(diào)節(jié)過程中的便捷性，根據(jù)相關(guān)資料顯示這兩組增益的整定可以具體的轉(zhuǎn)化成控制器寬待和觀測器寬帶兩個參數(shù)的整定。

考慮到LESO，可以將A-LC的特征方程轉(zhuǎn)換成如下所示：

為了盡量簡潔可以假設(shè)所有的觀測器幾點都是配置在-wo之上，由此可以推出

在廣義擾動f（y，u，d）能夠準(zhǔn)確估計的情況下原系統(tǒng)會變成一個多重的積分模型，并且在較為接近的情況下可以得出如下的狀態(tài)反饋閉環(huán)特征方程

同理如果將所有的控制器極點都配置在-wc上的話可以得出

進(jìn)而得出

由此在對反饋控制律進(jìn)行增益的時候也只需要對單個參數(shù)wc進(jìn)行調(diào)節(jié)就可以。

由此我們可以發(fā)現(xiàn)LADRC的本質(zhì)上是屬于一種獨立于被控對象模型的具有較好的普適性的控制結(jié)構(gòu)，我們需要對對象的相對階r和相應(yīng)增益b來進(jìn)行了解。而LADRC只需要對2個參數(shù)進(jìn)行整定就可以極為簡單的被控制工程師所理解，并且這個結(jié)構(gòu)的本身又具備積分行為，綜上在對系統(tǒng)進(jìn)行設(shè)計的過程中不需要再額外的加入積分器。

3 結(jié)束語

本文主要針對供電負(fù)荷穩(wěn)定性優(yōu)化控制系統(tǒng)模型和線性自抗擾控制加以分析，并且針對電力系統(tǒng)之中所存在的非線性特性因素采用LADRC方法。文中主要研究電力系統(tǒng)供電負(fù)荷穩(wěn)定性的優(yōu)化控制策略，希望能夠使控制系統(tǒng)的性能得到有效的提高。對于諸如實際工業(yè)控制的過程中表現(xiàn)出的調(diào)速器死區(qū)或者發(fā)電速率約束以及限幅限速等問題努力尋找出一定的應(yīng)對方法，由此希望為電力行業(yè)良好發(fā)展提供一定的參考。