空間幾何中的創新問題聚焦

■劉大鳴(特級教師)

近幾年高考對空間幾何的考查始終是圍繞“空間問題平面化和模型化”展開的,下面對其創新問題進行聚焦。

創新1：由三視圖判斷幾何體的特征

例1 某四棱錐的三視圖如圖1所示,在此四棱錐的側面中,直角三角形的個數為____。

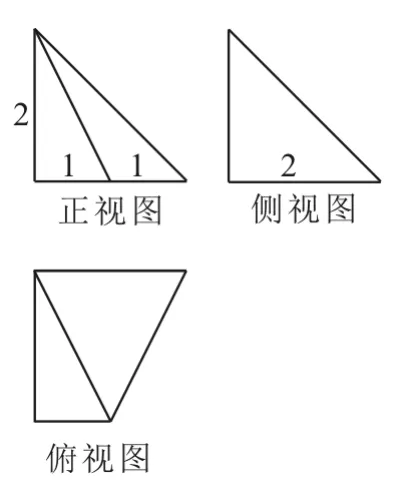
圖1

解：根據三視圖中有兩個直角三角形的特征來還原幾何體。由三視圖可得正方體內的四棱錐P-ABCD,如圖2所示。

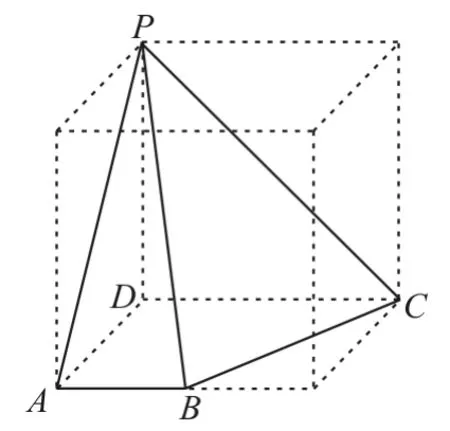
圖2

在四棱錐P-ABCD中,PD=2,AD=2,CD=2,AB=1,容易得到3個直角三角形,即△PAD,△PCD,△PAB。答案為3。

回味：由三視圖判斷幾何體的特征的關鍵是正確還原出直觀圖,在還原直觀圖時要利用三視圖的特征:正俯一樣長,俯側一樣寬,正側一樣高。

變式1：某幾何體的三視圖如圖3所示(單位:cm),則該幾何體的體積(單位:cm3)是____。

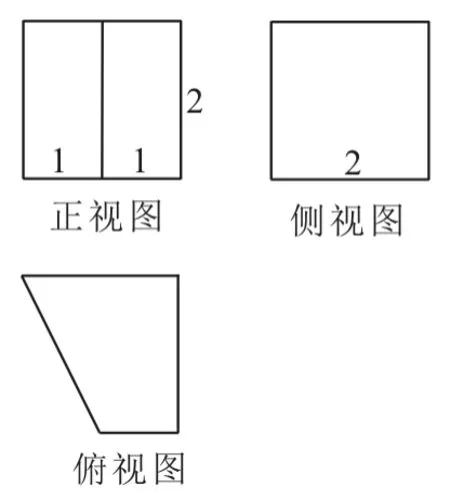
圖3

提示：根據三視圖可知該幾何體為一個直四棱柱。直四棱柱的高為2,底面為直角梯形,梯形的上下底的邊長分別為1,2,梯形的高為2,因此該幾何體的體積為6。

創新2：旋轉體的表面積或體積的計算

例2 如圖4,已知圓錐的頂點為S,母線SA,SB所成角的余弦值為,SA與圓錐底面所成的角為45°,若△SAB的面積為5,則該圓錐的側面積為 。______

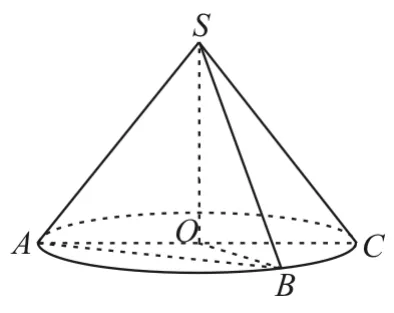
圖4

解：根據條件求出圓錐的母線SA,SB及底面圓的半徑長,再利用圓錐的側面積公式求解。設S在底面上的射影為O,底面半徑為r,則SO⊥底面ABO。

回味：解答本題的關鍵是找出母線與底面所成的角及兩母線的夾角,利用平面幾何知識求出相應線段的長。

變式2：如圖5,已知圓錐的頂點為S,母線SA,SB互相垂直,SA與圓錐底面所成的角為,若△SAB的面積為8,則該圓錐的體積為____。

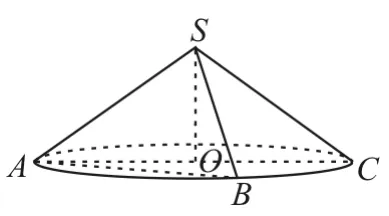
圖5

創新3：幾何體的表面積或體積的計算

例3 如圖6所示,正方體的棱長為2,以其所有面的中心為頂點的多面體的體積為___。

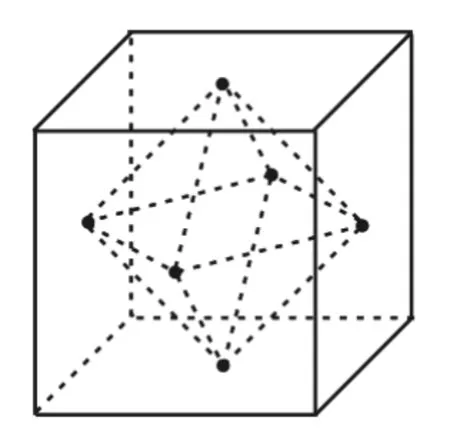
圖6

解：先分析組合體的構成,確定錐體的高,再利用錐體的體積公式求出結果。由圖6可知,該多面體為兩個全等正四棱錐的組合體。正四棱錐的高為正方體棱長的一半即為1,底面正方形的邊長為2,所以該多面體的體積

回味：求解組合體的體積問題,關鍵是準確理解幾何體的定義,真正把握幾何體的結構特征。本題其實是求正八面體的體積,可將正八面體分割為兩個全等的正四棱錐求解。

變式3：如圖7,已知正方體的棱長為1,除面ABCD外,該正方體其余各面的中心分別為點E,F,G,H,M,則四棱錐M-EFGH的體積為_________。

圖7

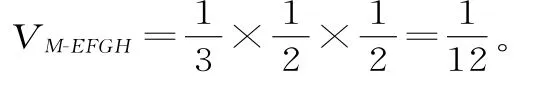
創新4：“平移法”求解異面直線所成的角

例4 如圖8,在四面體ABCD中,△ABC是等邊三角形,平面ABC⊥平面ABD,點M為棱AB的中點,AB=2,AD=23,∠BAD=90°。

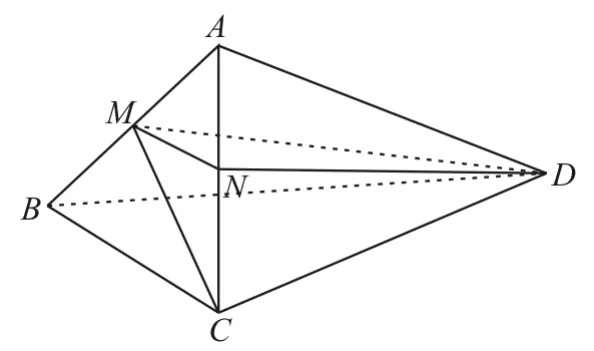
圖8

(1)求證:AD⊥BC。

(2)求異面直線BC與MD所成角的余弦值。

解：由面面垂直證明線面垂直,進而得到線線垂直,再利用中位線得到異面直線所成的角。

(1)由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC。

(2)取AC的中點為N,連接MN,ND。由M為棱AB的中點,可知MN∥BC,所以∠DMN為異面直線BC與MD所成的角。

由AD⊥平面ABC,可得AD⊥AC。在Rt△DAN 中,由AN=1,可得DN=

回味：已知兩條異面直線a,b,經過空間任一點O作直線a"∥a,b"∥b,a",b"所成的角的大小與點O的位置無關,把a",b"所成的銳角(或直角)叫作異面直線a,b所成的角(或夾角)。為了簡便,點O通常取在異面直線的一條上。

變式4：如圖9所示,在正方體ABCDA1B1C1D1中,E為棱CC1的中點,則異面直線AE與CD所成角的正切值為______。

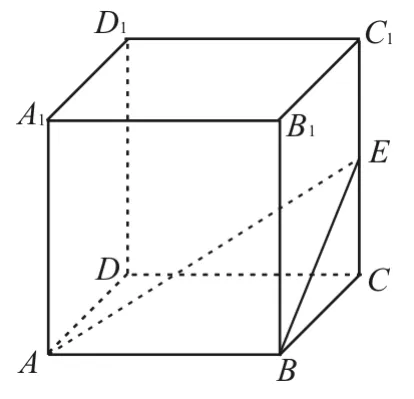
圖9

提示：在正方體ABCD-A1B1C1D1中,由于CD∥AB,所以異面直線AE與CD所成的角為∠EAB。設正方體的邊長為2a,由E為棱CC1的中點,可得CE=a,BE=5a,所以tan

創新5：利用面面垂直的性質定理作“點到平面的距離”

例5 如圖10所示,已知正方體ABCD-A1B1C1D1的棱長為1,則四棱錐A1-BB1D1D的體積為____。

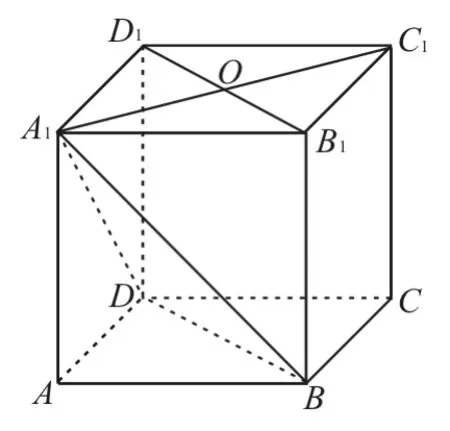
圖10

解：要求四棱錐的體積,需求四棱錐的底面積和高,因此解答本題的關鍵是利用面面垂直的性質定理確定平面外的點在該平面上的射影位置。連接A1C1交B1D1于點O,由平面A1B1C1D1⊥平面BDD1B1,A1C1⊥D1B1,可知A1C1⊥平面BDD1B1,則A1O就是四棱錐A-BBDD的高。由AO=×AC=111111

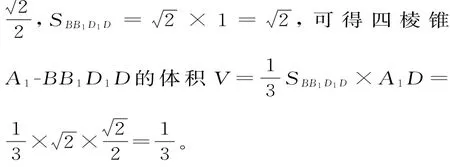
回味：解答本題的關鍵是挖掘題設中面面垂直的條件,尋找所求四棱錐的高。本題的解題過程凸顯“空間問題平面化”的特點。

變式5：如圖11,在三棱錐P-ABC中,AB=BC=22,PA=PB=PC=AC=4,O為AC的中點。

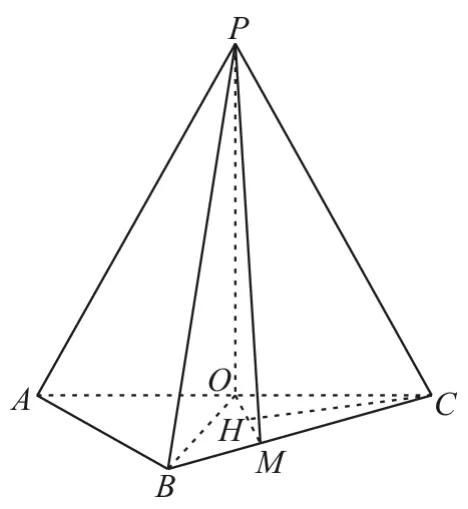
圖11

(1)證明:PO⊥平面ABC。

(2)若點M在棱BC上,且MC=2MB,求點C到平面POM的距離。

提示：(1)因為AP=CP=AC=4,O為AC的中點,所以OP⊥AC,且OP=23。

由上可得OP2+OB2=PB2,所以OP⊥OB。由于OP⊥OB,OP⊥AC,OB∩AC=O,所以PO⊥平面ABC。

(2)作CH⊥OM,垂足為H。

由(1)可得OP⊥CH,平面POM⊥平面COM。由面面垂直的性質定理知CH⊥平面POM,所以CH即為點C到平面POM的距離。

創新6：空間中“平行與垂直”的證明方法

例6 如圖12,矩形ABCD所在平面與半圓弧CD所在平面垂直,M是弧CD上異于C,D的點。

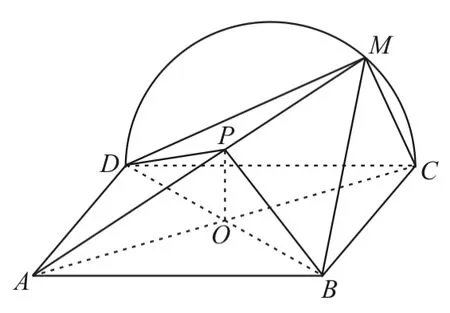
圖12

(1)證明:平面AMB⊥平面BMC。

(2)在線段AM上是否存在點P,使得MC∥平面PBD?請說明理由。

解：(1)由題設知,平面CMD⊥平面ABCD,交線為CD。

因為BC⊥CD,由面面垂直的性質定理可得BC⊥平面CMD,故BC⊥DM。

因為M為弧CD上異于C,D的點,且DC為直徑,所以DM⊥CM。

又因為BC∩CM=C,所以DM⊥平面BMC。而DM?平面AMD,故平面AMD⊥平面BMC。

(2)當P為AM的中點時,MC∥平面PBD。證明如下:

連接AC交BD于O。因為ABCD為矩形,所以點O為AC的中點。

連接OP。因為P為AM的中點,所以MC∥OP。因為MC?平面PBD,OP?平面PBD,所以MC∥平面PBD。

回味：證明面面關系的核心是證明線面關系,證明線面關系的核心是證明線線關系。同學們要掌握線線平行、線面平行、線線垂直、線面垂直的證明方法。

變式6：如圖13,在平行六面體ABCDA1B1C1D1中,AA1=AB,AB1⊥B1C1。

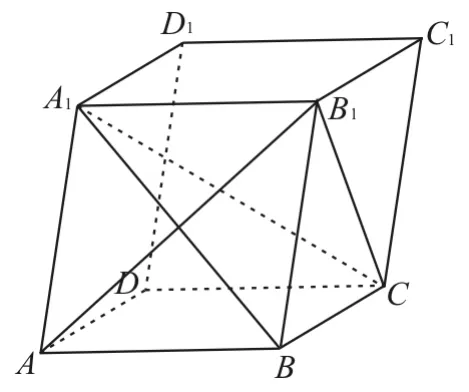
圖13

求證:(1)AB∥平面A1B1C。

(2)平面ABB1A1⊥平面A1BC。

證明：(1)在平行六面體ABCDA1B1C1D1中,AB∥A1B1。

因為AB?平面A1B1C,A1B1?平面A1B1C,所以AB∥平面A1B1C。

(2)在平行六面體ABCD-A1B1C1D1中,四邊形ABB1A1為平行四邊形。

因為AA1=AB,所以四邊形ABB1A1為菱形,可知AB1⊥A1B。

因為AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC。因為A1B∩BC=B,A1B?平面A1BC,BC?平面A1BC,所以AB1⊥平面A1BC。

又因為AB1?平面ABB1A1,所以平面ABB1A1⊥平面A1BC。