點、直線、平面之間的位置關系常見典型考題賞析

■王立超

點、直線、平面之間的位置關系是立體幾何的重要知識,也是高考的常考知識。下面主要介紹空間中的點、直線、平面之間的位置關系的典型例題的解題思想與方法,供大家學習與參考。

題型一：平面的基本性質及應用

點線共面問題的兩種證明方法:①納入平面法,即先確定一個平面,再證有關點線在此平面內。②輔助平面法,即先證有關點線確定平面α,再證其余點線確定平面β,最后證明平面α,β重合。證明多線共點問題,常用的方法是先證其中兩條直線交于一點,再證交點在第三條直線上,證交點在第三條直線上時,第三條直線應為前兩條直線所在平面的交線。

例1 如圖1所示,在正方體ABCDA1B1C1D1中,O為正方形ABCD的中心,H為直線B1D與平面ACD1的交點。求證:D1,H,O三點共線。

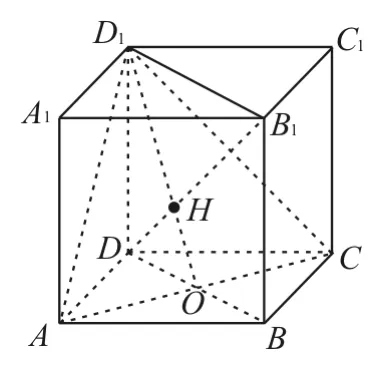
圖1

證明：因為BB1DD1,所以四邊形BB1D1D為平行四邊形。又H∈B1D,B1D?平面BB1D1D,則H∈平面BB1D1D。

因為平面ACD1∩平面BB1D1D=OD1,所以H∈OD1,即D1,H,O三點共線。

跟蹤訓練1：如圖2所示,已知正方體ABCD-A1B1C1D1中,E,F分別是AB和AA1的中點。

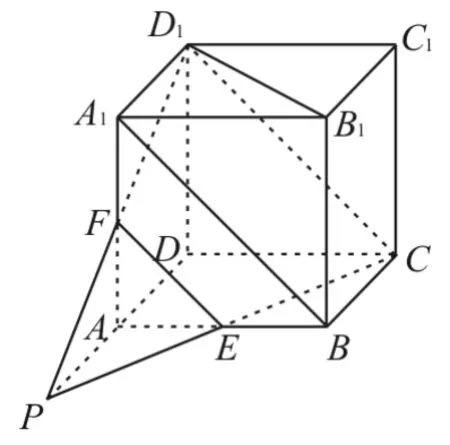
圖2

求證:(1)E,C,D1,F四點共面。

(2)CE,D1F,DA三線共點。

提示：(1)連接EF,CD1,A1B。因為E,F分別是AB,AA1的中點,所以EF∥BA1。又A1B∥D1C,所以EF∥CD1。所以E,C,D1,F四點共面。

(2)因為EF∥CD1,EF＜CD1,所以CE與D1F必相交,設交點為P。

由P∈CE,CE?平面ABCD,可得P∈平面ABCD。同理可得P∈平面ADD1A1。

又平面ABCD∩平面ADD1A1=DA,所以P∈直線DA,可知CE,D1F,DA三線共點。

題型二：異面直線所成的角

用平移法求異面直線所成的角的三步法:一作,即根據定義作平行線,作出異面直線所成的角;二證,即證明作出的角是異面直線所成的角;三求,即解三角形,求出作出的角,如果求出的角是銳角或直角,則它就是要求的角,如果求出的角是鈍角,則它的補角才是要求的角。

例2 如圖3,在底面為正方形,側棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AA1=2AB=2,則異面直線A1B與AD1所成角的余弦值為( )。

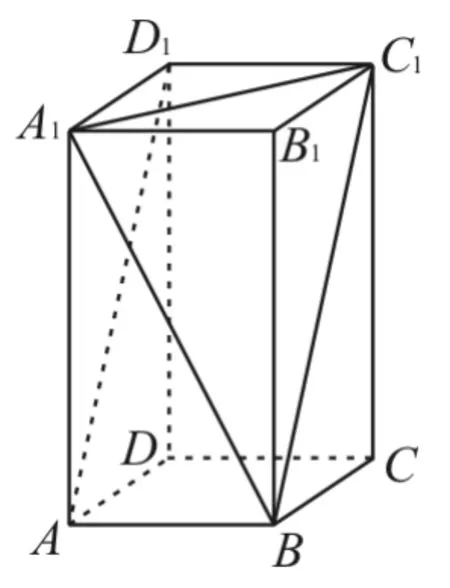
圖3

解：由題意可得BC1∥AD1,則∠A1BC1即為異面直線A1B與AD1所成的角。由AB=1,AA1=2,易得A1C1=,A1B=即異面直線AB與AD所成角的余弦11值。應選D。

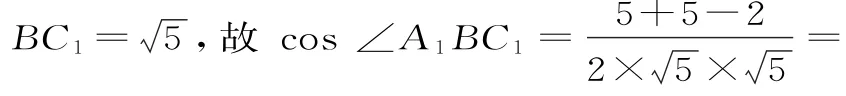
跟蹤訓練2：直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,則異面直線BA1與AC1所成的角等于( )。

A.30° B.45°

C.60° D.90°

提示：如圖4,延長CA到點D,使得AD=AC,則四邊形ADA1C1為平行四邊形,所以∠DA1B就是異面直線BA1與AC1所成的角。又A1D=A1B=DB,所以△A1DB為等邊三角形,所以∠DA1B=60°。應選C。

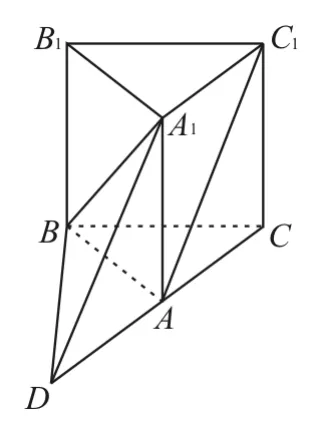
圖4

題型三：垂直關系的基本問題

垂直關系的基本問題包括線線垂直、線面垂直、面面垂直問題。證明直線與平面垂直的常用方法:①利用判定定理。②利用判定定理的推論(a∥b,a⊥α?b⊥α)。③利用面面平行的性質(a⊥α,α∥β?a⊥β)。④利用面面垂直的性質,即當兩個平面垂直時,在一個平面內垂直于交線的直線垂直于另一個平面。判斷面面垂直的方法:①利用面面垂直的定義。②利用面面垂直的判定定理(a⊥β,a?α?α⊥β)。

例3 已知m和n是兩條不同的直線,α和β是兩個不重合的平面,下面給出的條件中一定能推出m⊥β的是( )。

A.α⊥β,且m?α

B.m∥n,且n⊥β

C.α⊥β,且m∥α

D.m⊥n,且n∥β

解：因為α⊥β,m?α,則m,β的位置關系不確定,即可能平行、相交或m在β面內,A錯誤。由線面垂直的性質定理可知B正確。若α⊥β,m∥α,則m,β的位置關系不確定,C錯誤。若m⊥n,n∥β,則m,β的位置關系也不確定,D錯誤。應選B。

跟蹤訓練3：已知a,b,c為三條不同的直線,且a?平面α,b?平面β,α∩β=c。

①若a與b是異面直線,則c至少與a,b中的一條相交;

②若a不垂直于c,則a與b一定不垂直;

③若a∥b,則必有a∥c;

④若a⊥b,a⊥c,則必有α⊥β。

其中正確命題的個數是( )。

A.0 B.1

C.2 D.3

提示：若a與b是異面直線,則c至少與a,b中的一條相交,①正確。當α⊥β時,若b⊥c,則b⊥平面α,此時不論a,c是否垂直,均有a⊥b,②錯誤。當a∥b時,則a∥平面β,由線面平行的性質定理可得a∥c,③正確。若b∥c,則當a⊥b,a⊥c時,a與平面β不一定垂直,此時平面α與平面β也不一定垂直,④錯誤。應選C。

題型四：等體積法求點到平面之間的距離

用等體積法求點到平面之間的距離時,通過變換頂點和底面,轉化為底面和高都易求的錐體體積。

例4 如圖5,在直三棱柱ABC-DEF中,底面ABC的棱AB⊥BC,且AB=BC=2。點G,H在側棱CF上,且CH=HG=GF=1。

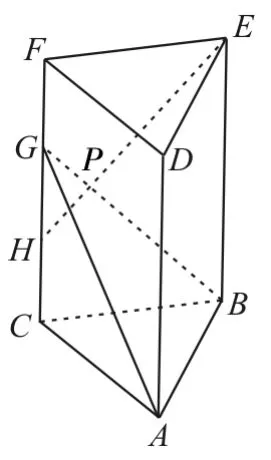
圖5

(1)證明:EH⊥平面ABG。

(2)求點C到平面ABG的距離。

解：證明直線與平面垂直,只需證明直線與平面內的兩條相交直線垂直即可;等體積法是求點到平面之間距離的常用方法。

(1)因為ABC-DEF是直三棱柱,所以FC⊥平面ABC。而AB?平面ABC,所以FC⊥AB。因為AB⊥BC,BC∩FC=C,所以AB⊥平面BCFE。又因為EH?平面BCFE,所以AB⊥EH。

由題設知△EFH與△BCG均為直角三角形,因為EF=2=FH,BC=2=CG,所以∠EHF=45°,∠BGC=45°。設BG∩EH=P,則∠GPH=90°,即EH⊥BG。

又因為AB∩BG=B,所以EH⊥平面ABG。

因為CG⊥平面ABC,所以VG-ABC=×

跟蹤訓練4：如圖6,已知三棱錐A-BCD中,△ABC是等腰直角三角形,AC⊥BC,BC=2,AD⊥平面BCD,AD=1。

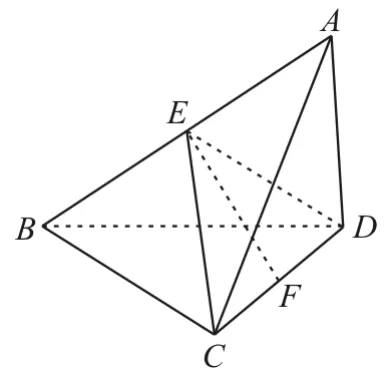
圖6

(1)求證:平面ABC⊥平面ACD。

(2)若E為AB的中點,求點A到平面CED的距離。

提示：(1)因為AD⊥平面BCD,BC?平面BCD,所以AD⊥BC。又因為AC⊥BC,AC∩AD=A,所以BC⊥平面ACD。由BC?平面ABC,可知平面ABC⊥平面ACD。

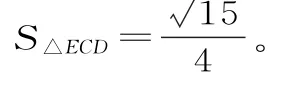
由(1)知BC⊥平面ACD,所以點E到平面ACD的距離為1,且

題型五：立體幾何中的存在性問題

對于線面關系中的存在性問題,首先假設存在,然后在該假設條件下,利用線面關系的相關定理、性質進行推理論證,尋找假設滿足的條件,若滿足則肯定假設,若得出矛盾的結論則否定假設。

例5 如圖7,在四棱錐P-ABCD中,△PAD為正三角形,平面PAD⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB=2AD=4。

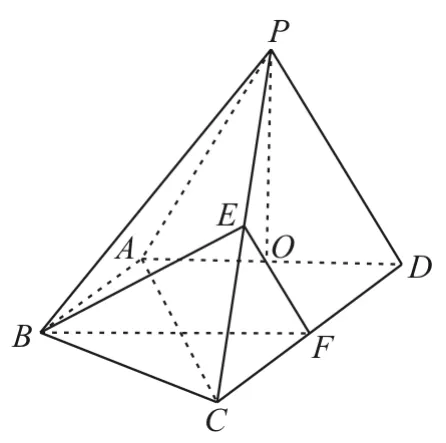
圖7

(1)求證:平面PCD⊥平面PAD。

(2)求三棱錐P-ABC的體積。

(3)在棱PC上是否存在點E,使得BE∥平面PAD?若存在,請確定點E的位置并證明;若不存在,請說明理由。

解：(1)因為AB∥CD,AB⊥AD,所以CD⊥AD。

因為平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以CD⊥平面PAD。

又因為CD?平面PCD,所以平面PCD⊥平面PAD。

(2)取AD的中點為O。因為△PAD為正三角形,所以PO⊥AD。

因為平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,所以PO⊥平面ABCD,即PO為三棱錐P-ABC的高。

因為△PAD為正三角形,CD=2AB=2AD=4,所以PO=3。

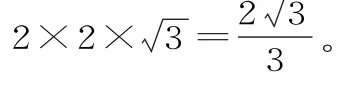
(3)在棱PC上存在點E,當E為PC的中點時,BE∥平面PAD。證明如下:

取CP,CD的中點分別為E,F,所以EF∥PD。

因為AB∥CD,CD=2AB,所以AB∥FD,AB=FD,可知四邊形ABFD為平行四邊形,所以BF∥AD。

因為BF∩EF=F,AD∩PD=D,所以平面BEF∥平面PAD。

因為BE?平面BEF,所以BE∥平面PAD。

跟蹤訓練5：如圖8,在四棱錐P-ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=2。

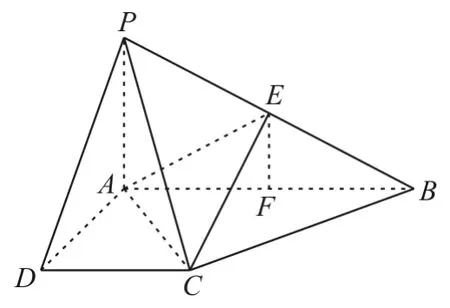
圖8

(1)求證:平面PAD⊥平面PCD。

(2)試在棱PB上確定一點E,使截面AEC把該幾何體分成的兩部分PDCEA與EACB的體積比為2∶1。

提示：(1)因為AD⊥AB,DC∥AB,所以DC⊥AD。

因為PA⊥平面ABCD,DC?平面ABCD,所以DC⊥PA。

因為AD∩PA=A,AD、PA?平面PAD,所以DC⊥平面PAD。

又因為DC?平面PCD,所以平面PAD⊥平面PCD。

(2)作EF⊥AB于點F。因為在△ABP中,PA⊥AB,所以EF∥PA,所以EF⊥平面ABCD。

由AD=1,AB=2,BC=2,易得CD=1,所以V四棱錐P-ABCD

由VPDCEA∶V三棱錐E-ACB=2∶1,可 得∶h=2∶1,解得h=,所以E=PA,可知E為PB的中點。