淺談“構造法”在解題中的妙用
(湖北省嘉魚縣教研室 湖北嘉魚 437200)
構造法是運用數學的基本思想經過認真的觀察,深入的思考、分析,遷移聯想,正確思維,巧妙地、合理地構造出某些元素、某種模式,使問題轉化為新元素的問題,或轉化為新元素之間的一種新的組織形式,從而使問題得以解決,這種方法稱之為“構造法” .
怎樣構造呢?構造法的內涵十分豐富,沒有完全固定的模式可以套用,它是以廣泛抽象的普遍性與現實問題的特殊性為基礎,針對具體問題的特點而采取的相應的解決方法,基本的方法是:借用一類問題的性質,來研究另一類問題的思維方法,在解題過程中,若按習慣定式思維去探求解題途徑比較困難時,我們可以根據題目特點,展開豐富的聯想拓寬自己的思維,運用構造法解題也是培養我們創新意識和創新思維的手段之一,同時對提高我們的解題能力也有所幫助。[1]
案例:人教版八(上)教材第130頁第11題:一次越野賽跑中,當小明跑了1600米時,小剛跑了1450米,此后兩人分別以a米/秒和b米/秒勻速跑,又過100秒時小剛追上小明,200秒時小剛到達終點,這次越野賽跑的全程為多少?[2]
思考:本題從表面上似乎與函數沒有關聯,但卻可以構造函數關系并運用函數的相關知識予以解決,由于小明和小剛兩人是勻速跑,我們可以將路程y看成是時間x的一次函數,依題意可畫出如下函數圖象(圖1):
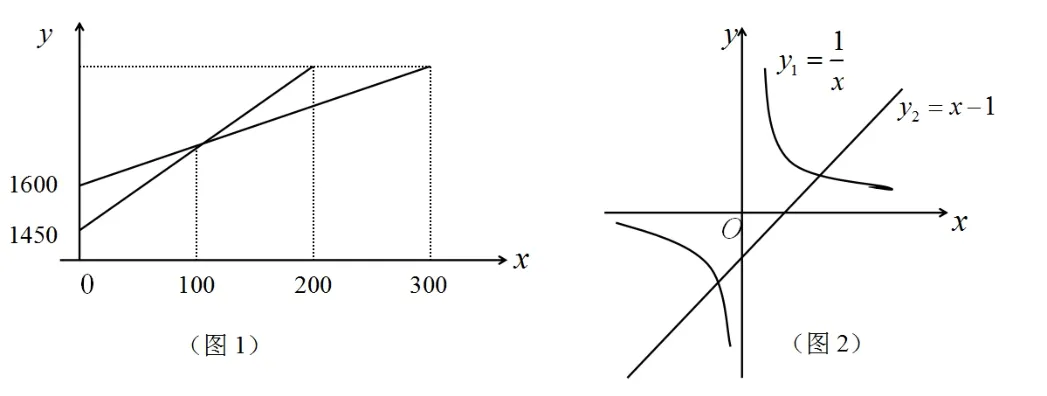
根據函數圖象,可設y1=bx+1450,y2=ax+1600,當x=100時,y1=y2;當x=200時對應的與x=300時對應的相等,及100a+ 1600=100b+1450,200b+ 1450=300a+1600,聯立解得a=1.5,b=3,故此次越野跑的全程為:200×3+1450=2050.
回顧本題的解答過程,通過巧妙地構造一次函數并通過函數圖象形象、直觀地使問題得以解決,思維活躍,解法新穎,令人回味!
思考:盡管本道題超出了課程標準要求(可化為一元二次方程的分式方程問題),但我們仍能打破常規,從中體會到構造法的妙用!可以將方程兩邊分別
反思:本道題的初衷是將分式方程轉化為一元二次方程,再通過判斷一元二次方程解的個數得到原分式方程解的個數,可在上述解決問題過程中,通過構造兩個函數,將判斷方程解的個數問題轉化為判斷兩個函數圖象交點個數問題,既體現了方程與函數的本質聯系,又發散了思維,培養了創新意識,數學課程標準(2011版)明確指出,創新意識的培養應該從義務教育階段做起,貫穿數學教育的始終,而創新意識正是學生所缺乏的.我們不能錯失這樣的好機會!
可以看到,構造法雖然算不上是解決數學問題的一般方法,其技巧性較強,但是在數學很多領域都有它的身影,只要我們發散思維,豐富聯想,合理構造,勇于創新,它就在你身邊!對“構造法”的理解和運用有助于我們打破思維定勢,完善思維品質,達到解題境界上的升華!

