微積分在經濟學中的應用

（東莞市技師學院 廣東東莞 523000）

引言

數學是一科重要而且極為基礎的學科，把數學的研究思想引入到經濟學里，為經濟學的研究提供了簡便與適用的方法，由計數、計算對事物變化的觀察中產生。隨著數學這個學科的發展，數學已經逐步的深入到各個領域。在經濟學和金融學等學科中，數學更是發揮了及其重要的作用[1]。用數學理論研究宏觀經濟學、微觀經濟學，用數學模型進行風險預測與分析，已經越來越普遍。隨著近現代微積分理論的發展，經濟學也在經歷著飛速的變化，微積分是由于生產技術的進步、經濟社會的發展而產生的。特別是隨著計算機的廣泛應用，建立微積分模型來解決經濟學問題，成為了實現高效決策和精確決策的重要途徑。微積分等數學知的運用是在經濟學問題的研究中努力的方向和目標。

一、導數在彈性供給問題分析

微積分是微分學和積分學的統稱，它的萌芽、發生與發展經歷了漫長的時期。早在古希臘時期，歐多克斯提出了窮竭法。這是微積分的先驅，而我國莊子的《天下篇》中也有 “ 一尺之錘，日取其半，萬世不竭 ” 的極限思想，公元 263 年，劉徽為《九間算術》作注時提出了 “割圓術 ”，用正多邊形來逼近圓周。這是極限論思想的成功運用。積分概念是由求某些面積、體積和弧長引起的，古希臘數學家要基米德在《拋物線求積法》中用究竭法求出拋物線弓形的面積，人沒有用極限，是 “ 有限 ” 開工的窮竭法。但阿基米德的貢獻真正成為積分學的萌芽。微分是聯系到對曲線作切線的問題和函數的極大值、極小值問題而產生的。微分方法的第一個真正值得注意的先驅工作起源于 1629 年費爾瑪陳述的概念，他給同了如何確定極大值和極小值的方法。需求價格彈性指的是某商品的需求量對其價格變動的反應程度。它可以用價格系數來表示[2]。本小節主要分析供給彈性問題，其中導數對供給彈性問題的影響。所謂供給彈性，表示一定時期的一種商品的供給量的相對變動對于該商品的價格的相對變動的反應程度[3]。其中，供給彈性是用來表示商品供給量的變動率對于價格的變動率的反應程度的。若供給函數為Q=f(p)，則供給價格彈性記做Es，定義為

一般地，假設函數Q=f(p)是單調增加的，由于f′(p)＞0，p＞0，f(p)＞0，所以供給價格彈性Es取正值，供給價格彈性簡稱供給彈性。

市場需求函數為Q需=1 2 -p2，市場供給函數為Q供=p2+4，當市場達到均衡（需求量等于銷售量）時，供給彈性是多少？

解 由于供給彈性是供給函數的導數，根據（1.4）及已知條件可知Q供=p2+4，因此，供給彈性為

因為市場均衡時即為市場對該產品的需求量等于銷售量，即Q需=Q供時達到市場均衡，因此知1 2 -p2=p2+4，解得p2=-2（舍），于是

Es=2 × 2=4，即市場均衡時供給彈性為4。

影響產品供給彈性的因素有很多，例如當增加產品所需消耗的生產要素費用過大時，該產品的彈性系數較小，反之則較大。此外，生產產品的時間長短也是影響產品供給彈性的因素之一，若短時期內廠商只能在固定的廠房設備下增加產量，此時供給量變化有限，則該產品彈性較小，反之較大。

二、微積分學在實際問題中的應用

1.成本控制問題應用

（3）產量為多少時，平均成本最低。

解：由于平均成本是邊際成本的原函數，所以對邊際平均成本函數積分便可以得到平均成本函數因此有

（1） 已知邊際成本函數，求總成本函數。

設用函數M C表示邊際成本函數，表示平均成本，Q為產量，C(Q)為總成本，則

（2）因為總成本函數等于平均成本函數與產量Q的乘積，即

積分學在經濟學中的應用十分普遍且起到重要作用，尤其是在已知邊際函數求原函數的問題中。利用一元函數積分學可以方便快捷的求出原函數，使得經濟問題的求解方法更加多樣化。同時，也使數學領域中一元函數積分學的運用范圍更加廣闊。

2.分期付款問題應用

王明是一名大一的學生，他想兼職并且利用分期付款的方式買一部手機，他了解到:某手機店對他想買的那種型號的手機進行付款銷售。手機的銷售定價是4000人民幣。分期購買時，分期36月，月還款額為150元。銀行貸款信息為，低于5000的貸款，年利率為15%（36月內）。試問，該選擇銀行貸款，還是分期付款？

解:

如果貸款，三年還清，那么王明每月要還款

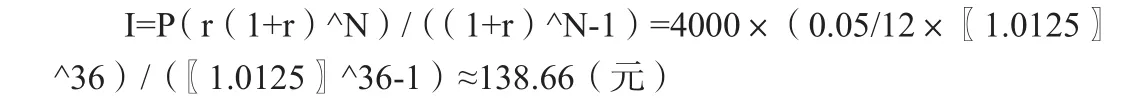
這里r=（（0.15））?12=0.125為月利率。計算結果表明，王明應該以貸款（每月還款139元）而不是分期付款（每月還款150元）的方式來購得他想買的該型號的手機。

3.利潤最大化問題應用

某種產品生產x件的邊際成本為C′(x)=5+0.2x元，固定成本2000元，又知每件產品的零售價為50元，試求產量x為多少時利潤最大？最大利潤值是多少？

解 因為變上限的定積分就是被積函數的一個原函數，因此可變成本就是總成本函數的變化率C′(x)在[0,x]上的定積分，又知固定成本為2000元，所以根據（2.1）有總成本函數

設銷售x件產品的收入函數為R(x)，依題意有：R(x)=50x。利潤函數l(x)為

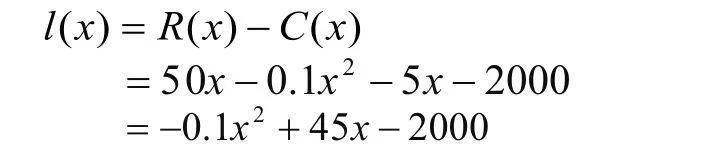
即產量為125時可獲得的最大利潤為2062.5元。

從以上例子中可以看出，利用定積分研究經濟函數，有助于實現利潤的最大化。

結語

本文介紹了微積分學知識在經濟學中的應用。利用微積分學知識可以對許多經濟學問題進行定量的分析，解決實際經濟問題，便于做出選擇和判斷。