高考函數審題易錯點總結

耿海艷

（武功縣普集高級中學 陜西咸陽 712200）

一、易錯點：用錯恒成立的條件

例1.已知函數f(x)=x2+ax+3-a若x∈[-2,2]時，f(x)≥0恒成立，求a的取值范圍．

錯解一：∵f(x)≥0恒成立，∴△=a2-4（3-a）≤0恒成立解得a的取值范圍為-6≤a≤2；

錯解二：∵f(x)=x2+ax+3-a若x∈[-2,2]時，f(x)≥0恒成立，

錯因：對二次函數f(x)=ax2+bx+c當x∈R上f(x)≥0恒成立時，△≤0”片面理解為“ax2+bx+c≥0，x∈[-2,2]恒成立時，△≤0”；

二、易錯點：函數單調性考慮不周致誤

錯解：(-∞，1)∪(1，+∞)

錯因分析：忽視了函數在定義域分界點上函數值的大小．

易錯突破：分段函數的單調性不僅要使函數在各個段上具有單調性，還要考慮分界點上函數值大小．

三、易錯點：混淆“過點”與“切點”致誤

例3.求過曲線y=x3-2x上的點(1，-1)的切線方程．

錯解：∵y'=3x3-2，∴k=y'|x=1=3×12-2=1，

∴切線方程為：y+1=x-1，即x-y-2=0.

錯因分析：混淆“過某一點”的切線和“在某一點處”的切線，錯把(1，-1)當做切點．

正解：設P(x0，y0)為切點，則切線的斜率為

解得x0=1，或x0=，故所求切線方程為y-(1-2)=(3-2)(x-1)。

易錯突破：過曲線上的點(1，-1)的切線與曲線的切點可能是(1，-1)，也可能不是(1，-1)．本題錯誤的根本原因就是把(1，-1)當成了切點．解決這類題目時，一定要注意區分“過點A的切線方程”與“在點A處的切線方程”的不同．雖只有一字之差，意義完全不同，“在”說明這點就是切點，“過”只說明切線過這個點，這個點不一定是切點．

四、易錯點：函數極值點概念不清致誤

例4.已知f(x)=x3+ax2+bx+a2在x=1處有極值為10，則a+b=______.

錯解：-7或0。

錯因分析：忽視了條件的等價性，“f'(1)=0”是“x=1為f(x)的極值點”的必要不充分條件。

正解：f'(x)=3x2+2ax+b，由x=1時，函數取得極值10，

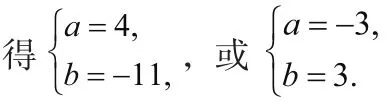
當a=4，b=-11時，f'(x)=3x2+8x-11=(3x+11)(x-1)在x=1兩 側 的 符號相反，符合題意。

當a=-3，b=3時，f'(x)=3(x-1)2在x=1兩側的符號相同，所以a=-3，b=3不符合題意，舍去。

綜上可知a=4，b=-11，∴a+b=-7。

易錯突破 ：對于可導函數f(x)：x0是極值點的充要條件是在x0點兩側導數異號，即f'(x)在方程f'(x)=0的根x0的左右的符號：“左正右負”?f(x)在x0處取極大值；“左負右正”?f(x)在x0處取極小值，而不僅是f'(x0)=0.f'(x0)=0是x0為極值點的必要而不充分條件．對于給出函數極大(小)值的條件，一定要既考慮f'(x0)=0，又考慮檢驗“左正右負”或“左負右正”，防止產生增根．

總之，不要急于攻難度大的“綜合題、探究題”，不要盲目地自己找題。精做題，審好題，才能做好題。要在解題的過程中，適時進行探究式、開放式題目的方法總結。明確自己在解題過程中運用到的知識點和整個解題思路。并加以自覺的應用。這樣每做一題在解題方式和思路上，都獲得積累。復習要真正地回到重視基礎的軌道上來，搞清基本原理、基本方法，體驗知識形成過程以及對知識本質意義的理解與感悟，同時，對基礎知識進行全面回顧，并形成自己的知識體系。