化歸思想在高中數學解題過程中的應用技巧

張宏量

（電子科技大學實驗中學 四川成都 610731）

引言

在高中的數學學習當中，作為學生的我們經常會遇到形式多樣的問題，想要更好的將這些問題全部解決掉最關鍵的就是應該學好數學知識。在數學知識的海洋當中，有很多類型的習題，只有在學習的過程中正確的掌握這些解題的思想，才能夠更加順利的將問題解決掉，我們也可以將這種正確的數學解題思想稱作為化歸思想。在高中階段的學習當中，我們能夠接觸到的化歸思想主要有數形結合思想、函數思想等，這些都是化歸思想，由此能夠看出，在高中數學的學習當中化歸思想的學習是較為核心的內容之一。因此，加強對化歸思想在高中數學解題過程中應用的研究具有十分重要的現實作用和意義。[1]

一、化歸思想在高中數學解題過程中的應用

1.化歸思想在高中數學函數解題過程中的應用

在高中數學階段的函數學習當中，我能夠深刻的認識到函數能夠充分體現當前世界當中的兩個不同變量之間存在的關系，在實際的解題過程當中，我們應該借助運動和變化的觀點，針對存在的關系加以深入的分析和探討，有效的將數學知識更加的抽象化。

[例1]已知二次函數y＝f（x）（x∈R）的圖像是一條開口向下且對稱軸為x＝3的拋物線，試比較大小：

（1）f（6）與f（4）

解 （1）∵y＝f（x）的圖像開口向下，且對稱軸是x＝3，∴x≥3時，f（x）為減函數，又6＞4＞3，∴f（6）＜f（4）

這道題考查的就是學生的對函數單調性的化歸和轉化的能力，這同樣也是高考當中非常容易考查的重點之一。

2.化歸思想在高中數學不等式解題過程中的應用

在我們高中階段的學習當中，不等式知識是較為基礎性的知識，但是也是高考當中考試的重點和重要的得分題。在解答不等式的過程中通常都是使用函數方程進行解答，這樣各個知識點之間就構成了比較復雜的問題。因此，在實際的解題當中，我們可以使用化歸思想進行解決，讓我們的解題思路變得更加的清晰。

先去掉絕對值號，再找它的等價組并求各不等式的解，然后取它們的交集即可

∴原不等式等價于不等式組

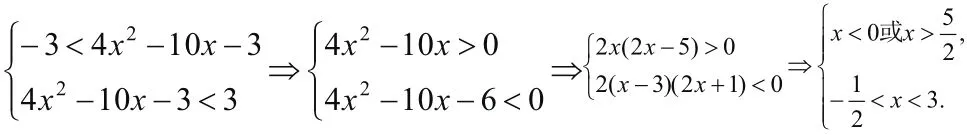
在解答題目當中還有絕對值的不等式的過程中，最關鍵的是應該將其轉化為不含有絕對值的不等是，然后在講不等是等價進行轉化成為不等式組，變成求解不等式組的解，通過應用化歸思想針對問題進行求解和轉化，能夠幫助學生更好的掌握相關不等式的知識點。

3.化歸思想在高中數學等比數列解題過程中的應用

一直以來，在高考的必考內容當中數列是其中之一，所以，我們在學習當中應該對數列知識加以重視。隨著等比數列等知識的深入學習，經常需要前項和前n項和得出通項公式來更好的解決這些問題。根據遞推工時獲得數列的通常公式也是高考當中經常出現的，遞推數列的通項公式相關問題能夠轉化為等比數列問題，能夠充分的體現數學的化歸思想。

二、高中生掌握化歸思想解決數學難題的方法以及對策

1.深入挖掘數學教材內容

教材不僅僅是我們學習知識的重要來源，同時還是能夠更好提升我們各項能力的重要途徑，是能夠開發我們思維的重要工具。因此，應該針對教材進行更加深層次的分析和挖掘，理解透其中包含的數學思想和方法。化歸思想本身屬于初等的數學思想和方法，但是其知識程度又高于普通的數學知識，因此，有很多的數學知識當中都包含著化歸思想和方法，我們在實際的學習當中應該結合教材當中的實際內同對隱性的思想進行挖掘，將教材當中所包含的數學思想全部挖掘出來，從而在學習當中不僅僅能夠學習到數學知識，還能夠了解更多的數學思想。[2]

2.加強學生自身變式練習

在課堂的學習當中，應該加強變式練習。變式練習實際上就是進行化歸的過程，基本上所有的變式都是將某一個未知的數學問題轉變為我們已經了解或者是掌握的問題，然后再針對這些問題加以有效的討論獲得解決的途徑。這樣的問題解決方法就是化歸思想。通過加強自身的變式練習，能夠讓解題當中的化歸思路更加明確，促使我們在學習當中能夠正確的掌握化歸的方向，因此，在實際的課堂學習當中，應該加強對變式的練習。[3]

3.堅持數學問題一題多解

問題是學習高中數學知識的“心臟”，很多的數學問題都是依靠我們自身的所掌握的方法以及思維進行及解決的，因此，我們在學習當中應該清楚，數學問題的解決思路和方法等都是多樣化的。當我們在實際的學習當中掌握了一種思維方式就能夠擁有更多的解題方案。在解決問題的過程中一題多解能夠從不同的角度對問題進行化歸，通過一題多解，能夠幫助我們在學習當中打開思路，提升化歸的能力。

4.深刻分析實際解題過程

針對老師在課堂上所講的知識，我們應該在掌握的基礎上對知識進行建構，只有這樣才能夠真正的掌握數學知識。如果僅僅是認識化歸的方法，或者是僅僅按照老師的示范加以模仿的并不是真正的理解了化歸思想。因此，應該在解題的過程當中創造機會，促使我們能夠更加深刻、真實的去發現、思考以及解決問題的全過程。當我們在雪中遇到復雜、生疏的問題時，應該先思考可以使用哪些化歸方法，如果沒有把握的時候可以針對每一種方式進行探索，如果遇到不能解決的問題可以向老師求救，在老師的正確引導下將問題徹底解決。

結語

綜上所述，在實際的高中數學學習當中，在解決數學問題當中，化歸思想都是一直存在的，化歸思想的存在能夠幫助我們在實際的學習當中將實際存在的問題轉化為數學知識，將較為復雜的問題變得更加的簡單化，將不熟悉的數學知識轉化為自己熟悉的知識。在實際的高中數學學習當中，我們應該清楚的認識到想要學好數學就應該在學習中不斷的增強自身的解題能力，想要更好的提升解題能力，就應該加強對基礎知識的學習，掌握一些最為基本的數學思想和解題方法。在以往的學習當中，我們經常會產生一個疑問“在課上時，老師講的都明白了，例題分析的也很清楚，但是當遇見條件稍微變化的問題時就不會解答了。”所以，在實際的學習當中，我們應該深入挖掘數學教材內容、加強學生自身變式練習、堅持數學問題一題多解、深刻分析實際解題過程，真正的能夠掌握解題的方法，促使自己的數學成績和數學能力都能夠獲得提高。