海洋湍流中光波特征參量和短期光束擴展的研究?

吳彤 季小玲 李曉慶 王歡 鄧宇 丁洲林

(四川師范大學物理與電子工程學院,成都 610068)

(2018年5月28日收到;2018年9月13日收到修改稿)

1 引 言

在湍流介質中光學傳遞函數取決于光波結構函數,而光波空間相干長度是表征湍流中光波結構函數的唯一參量,它在表征湍流強度和光傳輸相位校正技術中起著重要作用[1,2].目前,大氣湍流中光波特征參量(如光波結構函數、光波空間相干長度、Fried參數和光波閃爍指數等)的研究理論已較成熟.與大氣湍流不同,海洋湍流是由溫度和鹽度變化引起水折射率起伏而造成的[3].近年來,由于水下光通信、成像和傳感等應用的興起,海洋湍流對光波傳輸特性和成像特性影響的研究受到了極大的重視[4?16].2014年,Lu等[4]推導出了海洋湍流中波結構函數和空間相干長度的解析公式.2016年,Pu和Ji[5]推導出了海洋湍流中Fried參數的解析公式,并修正了用光學傳遞函數表征的海洋湍流中光成像模型.

然而,之前的研究[4?16]均采用了Nikishov等[3]建立的海洋湍流功率譜模型.值得指出的是,Nikishov等建立的海洋湍流功率譜模型存在一定的弊端,即該模型假設了海水有著穩定的分層,小密度層始終在大密度層之上.這樣,海水熱傳遞與鹽分轉移有相似的物理機制,此時渦流熱擴散率KT與渦流鹽擴散率KS被當作常數,甚至彼此相等(溫度和鹽度擴散對海水密度變化的影響相同),即渦流擴散率dr=KS/KT≡1[3].實際上,由于地表水受風和大氣熱交換的影響,海水通常不是穩定分層的,特別是在中高緯度地區,這種密度分層將會減少,甚至消失.2017年,Elamassie等[17]提出了新的海洋湍流功率譜模型,該模型考慮了實際水下環境中分層的不穩定性、溫度與鹽度的渦流擴散率彼此不相等的情況,因此更具合理性.本文基于Elamassie海洋湍流功率譜模型,重新推導出海洋湍流中光波結構函數、光波空間相干長度和Fried參數的解析公式,并校驗所得解析公式的正確性.研究發現,采用Elamassie海洋湍流功率譜模型與采用Nikishov海洋湍流功率譜模型所得結果差異很大.因此,本文研究結果具有重要意義.

另一方面,激光在湍流介質中傳輸要造成光束擴展和漂移.渦流小尺度引起的衍射效應造成光束擴展,渦流大尺度引起的折射效應造成光束漂移[1].光束漂移和光束擴展的綜合效應被稱為長期光束擴展,它包括短期光束擴展和光束漂移,是評估沿光路光強分布的主要參數之一[18].基于Nikishov等建立的海洋湍流功率譜模型,Lu等[19]研究了高斯光束在海洋湍流中的光束漂移,Yang等[20]研究了部分相干高斯光束在海洋湍流中的短期光束擴展.本文基于Elamassie海洋湍流功率譜模型,推導出準直和聚焦高斯光束短期光束擴展半解析公式,并驗證其正確性.研究還表明:海水穩定分層與否,短期光束擴展差異很大.需要指出的是,本文只研究光學湍流對光波特征參量和短期光束擴展的影響,未考慮其他復雜因素.

2 海洋湍流中光波特征參量

2017年,Elamassie等[17]建立了各向同性且非均勻海水介質中海洋湍流折射率起伏空間功率譜模型,即

其中, δ=8.284(κη)4/3+12.978(κη)2, κ是空間波數,η是Kolmogorov內尺度;ε表示海水單位質量湍流動能耗散率,其取值范圍為10?10—10?1m2/s3;χT表示海水溫度方差耗散率,其取值范圍為10?10—10?4K2/s;ω表示海洋湍流功率譜中溫度與鹽度起伏引起折射率變化貢獻的比率,其范圍取值為[?5,0],?5和0分別對應于溫度和鹽度變化引起的光學湍流[10];α是熱膨脹系數;C0=0.72,C1=2.35;AT=C0C?21P?1T,AS=C0C?21P?1S,ATS=0.5C0C?21P?1TS;PT和PS分別為溫度普朗特數和鹽度普朗特數,PTS=(PT+PS)/(PTPS).渦流擴散率dr定義為[17,21]

其中,KS和KT分別為渦流熱擴散率和鹽擴散率.渦流比RF是關于ω的分段函數[17]:

2000年,Nikishov等[3]建立的各向同性且均勻的海水介質中海洋湍流功率譜模型為

(4)式功率譜假設了渦流熱擴散率和鹽擴散率始終相等(即dr=KS/KT≡1),意味著海水有著穩定的分層(即小密度層始終在大密度層之上).但實際水下環境中,海水的分層一般是不穩定的.當dr≡ 1時,(1)式可化簡為(4)式,即(4)式是(1)式的特例.

圖1 海洋湍流功率譜模型Φn(κ)與Φn(κ)|dr≡1的相對差值?隨ω的變化Fig.1. Relative difference?of the power spectrum model of oceanic turbulence between Φn(κ)and Φn(κ)|dr≡1vs ω.

圖1給出了以上兩種海洋湍流功率譜模型的數值結果比較,其中

計算參數為η=1 mm,α=2.6×10?4l/deg,ε=10?5m2/s3, χT=10?7K2/s, κ =500,AT=1.863× 10?2,AS=1.9× 10?4和ATS=9.41×10?3.圖1表明:兩種海洋湍流功率譜模型差異很大.當|ω|>1時(即溫度變化引起的光學湍流占主導地位),Φn(κ)> Φn(κ)|dr≡1,Nikishov等的海洋湍流功率譜模型把湍流強度低估了;當|ω|<1時(即鹽度變化引起的光學湍流占主導地位),Φn(κ)< Φn(κ)|dr≡1,Nikishov等的海洋湍流功率譜模型把湍流強度高估了;當|ω|=1時(即溫度與鹽度引起的海水密度變化貢獻相同),Φn(κ)= Φn(κ)|dr≡1.

2.1 波結構函數與空間相干長度

Rytov近似下,各向同性且非均勻海水介質中,平面波的波結構函數可表示為[1]

其中,ρ為兩點間距;J0(·)為零階貝塞爾函數;L為傳輸距離;波數k=2π/λ,λ為光波波長.將零階貝塞爾函數展開成冪級數形式,并將(1)式代入(5)式后得到:

其中Γ(·)是伽馬函數,pFq(a1,···,ap,b1,···,bq;x)是一般超幾何函數,p和q均為正整數[1]. 可以證明,對于Elamassie功率譜(1)式及其各參數取值范圍,不等式成立.根據一般超幾何函數F和合流pq超幾何函數mFm(m為正整數)的定義,并依照文獻[4]中的推導方法,當海水鹽度為35%,溫度為20?C時(即PT≈ 7,PS≈ 700,AT=1.863×10?2,AS=1.9×10?4,ATS=9.41×10?3)[22],經過非常復雜的運算,我們得到海洋湍流中平面波波結構函數的解析表達式為

空間相干函數M(ρ,L)=exp[?D(ρ,L)/2],根據空間相干長度ρ0的定義M(ρ0,L)=e?1(即D(ρ0,L)=2)[1,2],并利用(9)式,可得到海洋湍流中平面波的空間相干長度ρ0,pl為

另一方面,Rytov近似下,各向同性且非均勻海水介質中球面波的波結構函數可表示為[1]

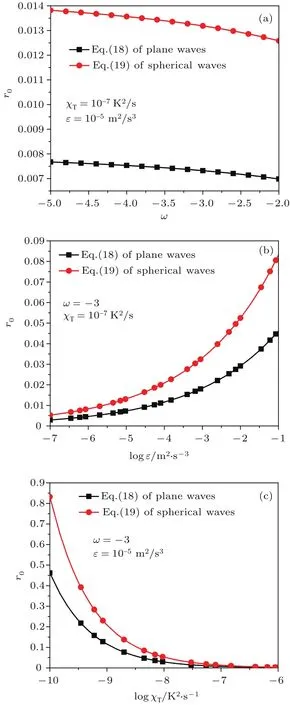
其中ξ=1?z/L是歸一化距離變量,z為可變距離(0

和海洋湍流中球面波的空間相干長度ρ0,sp為

可以證明:當α=2.6×10?4l/deg,η=1 mm和dr=1時,按照Elamassie海洋湍流功率譜模型推導出的波結構函數和空間相干長度的解析結果(即(9),(10),(12)和(13)式)可簡化為文獻[4]中相應的結果.因此,文獻[4]中的結果僅是本文研究結果的特例.

根據(9),(10),(12)和(13)式,可以得到

(14)式表明,按照Elamassie海洋湍流功率譜模型推導出的波結構函數在慣性范圍內依然滿足Kolmogorov三分之五定律,該結果與大氣湍流中的結果一致.

圖2 波結構函數D(ρ,L)的解析結果與積分結果的比較Fig.2.Comparison of the wave structure function D(ρ,L)between analytical results and integral results.

為了驗證本文得到解析結果的正確性,圖2給出了波結構函數的解析式與積分式的數值比較結果,計算參數為λ=0.417μm,L=30 m,η=1 mm,α=2.6×10?4l/deg和ρ ? η.圖2表明:波結構函數D(ρ,L)解析式(9)和(12)與積分式(5)和(11)的數值計算結果完全一致.此外,由圖2可知:ω,χT增大或ε減小,則D(ρ,L)增大,即海洋湍流增強;平面波波結構函數大于球面波波結構函數.

圖3 波結構函數D(ρ,L)與D(ρ,L)|dr≡1的相對差值?1隨ω的變化Fig.3.Relative difference?1of the wave structure function between D(ρ,L)and D(ρ,L)|dr≡1vs ω.

圖3給出了本文所得波結構函數解析結果與文獻[4]中對應結果(dr≡1)的比較,其中

計算參數為λ=0.417μm,L=30 m,η=1 mm,α =2.6× 10?4l/deg,ε=10?5m2/s3,χT=10?7K2/s,ρ =3 mm和ρ ? η. 圖3表明兩者差異很大,當|ω|>1時(即溫度變化引起的光學湍流占主導地位),D(ρ,L)>D(ρ,L)|dr≡1;當|ω|<1時(即鹽度變化引起的光學湍流占主導地位),D(ρ,L)

2.2 Fried參數

海洋湍流中長曝光成像分辨率可表示為[23]

其中,MTF0和MTFLE分別是透鏡調制傳遞函數和長曝光成像調制傳遞函數,?為空間角頻率.當滿足D0/ρ0? 1時(D0為光瞳孔徑),只考慮MTFLE的影響,忽略MTF0的影響[1],將(9)式代入長曝光成像調制傳遞函數MTFLE=exp[?D(λ?)/2]中,并考慮ρ = λ?[1],(15)式可簡化為極限分辨率Rmax,即

當滿足D0/ρ0?1時,只考慮MTF0的影響,忽略MTFLE的影響[1],(15)式可簡化為R0:

依據Fried參數r0的定義[23],將(17)式中的D0替換為r0,并令(16)式與(17)式相等,可得到平面波Fried參數r0,pl為

同理,可得球面波Fried參數r0,sp為:

可以證明:當α=2.6×10?4l/deg,η=1 mm和dr=1時,按照Elamassie海洋湍流功率譜模型推導出的Fried參數的解析結果(即(18)和(19)式)可簡化為文獻[5]中相應的結果.因此,文獻[5]中的結果僅是本文研究結果的特例.并且,比較2.2節與2.1節的結果,可以得到:r0,sp≈ 2.1ρ0,sp和r0,pl≈ 2.1ρ0,pl,該結果與大氣湍流中的結果一致.

圖4 Fried參數隨海洋湍流參數的變化 (a)ω;(b)ε;(c)χTFig.4.Curves of Fried parameter versus the oceanic turbulence parameters:(a)ω;(b)ε;(c)χT.

Fried參數隨海洋湍流參數變化曲線示于圖4,計算參數為λ=0.532μm,L=30 m,η=1 mm,α =2.6×10?4l/deg和ρ0? η.由圖4可知:ω,χT增大或ε減小,則r0減小,即湍流增強,光波相干性變差;平面波Fried參數小于球面波Fried參數.

圖5給出了本文所得Fried參數解析結果與文獻[5]中的對應結果(dr≡ 1)的比較,其中?2=(r0|dr≡1?r0)/r0,計算參數為λ =0.532μm,η=1 mm,α =2.6×10?4l/deg,ε=10?5m2/s3,χT=10?7K2/s,L=30 m和ρ0? η.圖5表明兩者差異很大.當|ω|>1時(即溫度變化引起的光學湍流占主導地位),r0r0|dr≡1,Nikishov海洋湍流功率譜模型把Fried參數值低估了,即海洋湍流強度被高估了;當|ω|=1時,r0=r0|dr≡1.

圖5 Fried參數r0與r0|dr≡1的相對差值?2隨ω的變化Fig.5.Relative difference?2between the Fried parameter r0and r0|dr≡1vs ω.

3 海洋湍流中短期光束擴展

海洋湍流中,長期光束擴展W2LT可以表示為[1]

其中,Λ=2L/(kW2)為接收端的光束菲涅耳比;HSS為小尺度濾波函數[1,25],

為強調光束緩變的自然特性,去掉(22)式中指數函數內的第一項,并且考慮幾何光學近似有[1]:

將Elamassie海洋湍流功率譜(1)式代入(21)式中,并考慮(23)式,短期光束擴展W2ST可表述為

其中,

將(26)式中的AT換成AS和ATS可分別得到?和ψ的表達式.

為校驗本文推導結果(25)式的正確性,圖6給出了短期光束擴展的半解析式(25)與積分式(21)隨傳輸距離L的變化曲線,計算參數為λ =0.532μm,η=1 mm,α =2.6×10?4l/deg和W0=0.1 m.圖6表明:短期光束擴展的半解析式(25)與積分式(21)的數值結果完全一致.此外,由圖6可知:短期光束擴展隨渦流擴散率dr而變化,海水穩定分層與否(dr=1與dr=1),光束短期光束擴展差異很大.

圖6 短期光束擴展隨L的變化 (a)準直光束;(b)聚焦光束Fig.6.Short-term beam spreadingvs L:(a)Collimated beam;(b)focused beam.

4 結 論

2000年,Nikishov等建立的海洋湍流功率譜模型中假設了海水有著穩定的分層.但是,受風和大氣熱交換的影響,實際海水通常不是穩定分層的,鹽度引起海水密度變化的貢獻與溫度的貢獻一般是不相等的,即渦流擴散率并非始終為1,而應是關于渦流熱擴散率和鹽擴散率的函數,體現出溫、鹽度變化對海水密度分層的影響.2017年,Elamassie等提出新的海洋湍流功率譜模型考慮了這一實際情況,該模型更為合理.本文基于Elamassie等的海洋湍流功率譜模型,重新推導出了海洋湍流中光波結構函數、光波空間相干長度和Fried參數的解析公式,并校驗了所得解析公式的正確性.研究發現:采用Elamassie海洋湍流功率譜模型與采用Nikishov海洋湍流功率譜模型所得結果差異很大.當溫度變化引起的光學湍流占主導地位時,Nikishov海洋湍流功率譜模型把湍流強度低估了;當鹽度變化引起的光學湍流占主導地位時,Nikishov海洋湍流功率譜模型把湍流強度高估了.并且,按照Elamassie海洋湍流功率譜模型推導出的波結構函數在慣性范圍內依然滿足Kolmogorov三分之五定律以及Fried參數與光波空間相干長度間依然滿足2.1倍關系,這與大氣湍流中的結果一致.此外,本文基于Elamassie海洋湍流功率譜模型,推導出了準直和聚焦高斯光束短期光束擴展的半解析公式,并驗證了其正確性.研究還表明:海水穩定分層與否,短期光束擴展差異很大.本文研究結果對水下湍流環境中的光通信、成像和傳感等應用具有重要意義.