同軸傳輸線微放電的統計理論穩態建模及敏感區域計算?

林舒 夏寧 王洪廣 李永東 劉純亮

(西安交通大學電信學院,電子物理與器件教育部重點實驗室,西安 710049)

(2018年7月10日收到;2018年9月21日收到修改稿)

1 引 言

微放電[1,2]是受微波場交互作用而在真空環境下產生的二次電子倍增效應,常發生于空間與加速器應用中的大功率微波器件,如微波開關、多工器與濾波器等[3?5].近年來,世界各航天強國相繼開展火星、金星以及太陽系其他小行星等探測計劃,而國內外的天基互聯網與星鏈計劃也對衛星通信與遙感技術的發展提出了更高的要求.作為星地通信與目標控制的惟一紐帶,星載通信系統的運行穩定性關乎整個空間任務的成敗.一方面,受空間遠距離通信衰減的影響,星載通信系統必須盡可能提高功率容量以保證通信質量.同時,空間有效載荷還要求盡可能地減小星載通信系統的質量與體積,以降低空間探測成本與設備研發周期,但這些趨勢都顯著增加了微波器件中發生微放電的風險.作為空間微波器件的主要失效模式,微放電輕則造成信號失諧與噪聲干擾,重則導致氣體放電并燒毀器件乃至通信系統,這也使得微放電成為限制空間通信技術發展的重要因素[6].因此,地面研制階段須準確預測微波器件的微放電閾值,并進行充分的抗微放電性能分析和設計,以盡可能降低在軌微波器件的微放電風險[7].

作為微放電研究的重要理論方法,統計理論可以充分考慮電子的出射與渡越隨機性[8],因而能夠實現準確的微放電機理分析與閾值預測.迄今為止,統計理論在微波器件的單、多載波微放電以及微波介質窗的倍增擊穿研究[9?11]中都有非常廣泛的應用.最早于2004年,Vdovicheva等通過推導微放電倍增條件的積分方程,構建得到微放電統計理論的穩態模型,由此實現平行平板傳輸線[12]與矩形波導[13]微放電的閾值計算與分析,但它只考慮了雙邊碰撞產生的二次電子發射.為此,Anza等在其基礎上構建用于模擬微放電動態發展過程的非穩態模型[14],并將其進一步推廣至平行平板傳輸線的多載波微放電分析中[15].非穩態模型由于同時考慮單邊和雙邊碰撞的影響,因而能夠獲得更高的微放電閾值計算精度.國內方面,浙江大學的宋慶慶等[16]也在其基礎上將統計理論與隨機漫步理論結合,由此實現矩形波導多載波微放電的非穩態建模與分析.同時為研究非對稱的微放電過程,本課題組又將非穩態建模推廣到同軸傳輸線微放電的機理分析與閾值計算中[17].

相比而言,非穩態模型雖然具有相對較高的閾值計算精度,但需要耗費大量計算時間模擬微放電的動態演化過程.因此,現有的非穩態模型主要用于離散頻點處同軸傳輸線微放電閾值的計算與比對,仍不適用于大范圍的微放電敏感區域計算.穩態模型則是通過微放電的穩態方程直接確定電子數目的變化趨勢,避免重復計算大量電子的運動軌跡,因而能夠實現更高的閾值計算效率.而在材料表面處理研究[18?20]方面,兼具高閾值計算精度與效率的穩態模型也可作為其微放電抑制效果的有效評估方法.為此,本課題組對平行平板微放電的穩態建模過程進行了改進,使其能夠兼顧微放電過程中的單邊碰撞,由此解決了穩態模型閾值計算精度低的問題[21].同時為更切合實際的工程應用需求,本課題組也曾對同軸結構微放電進行了近似的穩態建模[22],但由于未考慮其微放電過程的非對稱性,所得的閾值計算精度不甚理想.因此,當前亟需通過改進穩態建模構建精確有效的同軸傳輸線微放電閾值分析方法,并在其基礎上研究平行平板與同軸傳輸線的結構差異以及器件鍍膜材料對微放電閾值的影響規律,由此為實際工程中“免微放電”微波器件的設計與優化提供必要的參考.

鑒于此,本文在同時考慮微放電過程中單邊與雙邊碰撞影響的情況下,推導同軸結構中內、外導體處電子出射相位分布所滿足的穩態方程組,并提出一種通用的聯立迭代求解方法,構建同軸結構微放電統計理論的穩態模型.同時,使用該模型分別計算銀(Ag)、銅(Cu)、鋁(Al)與阿洛丁(Alodine)等常用工程鍍膜材料的同軸傳輸線微放電敏感區域以及不同徑比下的同軸傳輸線微放電閾值,并與歐空局(ESA)的微放電實驗結果進行對比驗證.最后與平行平板傳輸線微放電的敏感區域對比,分析平行平板與同軸結構微放電的閾值差異.

2 模型簡介

確切地說,完整的統計理論建模過程實際上包括兩個主要步驟.首先,推導電子軌跡的解析表達式,并在其基礎上構建聯合概率密度函數,由此實現電子渡越時間概率分布的求解計算;然后,通過微放電倍增過程的穩態或非穩態描述,計算給定條件下電子數目的變化趨勢,進而確定微放電的閾值與敏感區域.需要說明的是,微放電統計理論研究關注的是微放電建立的初始階段,因此下面的電子動力學分析會忽略空間電荷效應的影響.

2.1 基本方程及定義

圖1為同軸傳輸線的徑向剖面示意圖,其外導體的內半徑和內導體的外半徑分別用Ro和Ri表示,兩者比值(后面統一簡稱為徑比)為γ=Ro/Ri,同時內、外導體之間的距離為d=Ro?Ri.考慮到工程常用性以及現有同軸傳輸線微放電的實驗對象,本文默認選取50 ?特征阻抗的同軸傳輸線為研究對象,其物理尺寸為Ro=3.55 mm與Ri=1.54 mm,同時假設同軸傳輸線中的微波模式為TEM模,電子所受磁場力遠小于電場力,因此忽略磁場分量對電子運動的影響.另外,由于電子碰撞動能主要來自徑向電場Er的加速作用,所以這里僅分析徑向上的一維電子運動,而電子隨時間t變化的徑向位置r則可以通過如下方程求解:

其中me和e分別表示電子質量/kg與電量/C;Vrf是微波場的電壓幅值/V;ω是微波場的角頻率/rad·s?1.

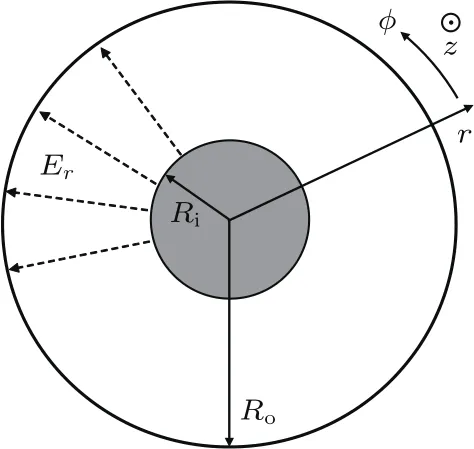
圖1 同軸傳輸線徑向剖面示意圖Fig.1.Diagrammatic cross-sectional view of coaxial transmission lines.

從數學角度上看,上述常微分方程并沒有精確的解析解.但在物理角度上,除時諧微波場使電子做快速振蕩運動以外,場分布非均勻性引起的勢能梯度還對電子產生米勒力的作用[23],它會推著電子同時朝外導體做緩慢漂移運動.因此采用微擾法(詳見文獻[24])可以近似推導得到如下電子軌跡的解析表達式:

式中的主要參數有

其中φs為電子出射相位;τ為電子碰撞時的相位變化量,其在廣義的時間量綱上又指電子的渡越時間;u,ηs和ηf分別表示歸一化的電子出射速度(υs)、出射位置(rs) 與碰撞位置(rf),等于υs/υω,ωrs/υω和ωrf/υω,并有υω=eVrf/meωrslnγ.由于電子的出射和碰撞位置均有可能為同軸結構的內導體或外導體處,所以這里將電子軌跡分為外導體處出射的單邊碰撞ξoo(rs=Ro與rf=Ro)、外導體處出射的雙邊碰撞ξoi(rs=Ro與rf=Ri)、內導體處出射的雙邊碰撞ξio(rs=Ri且rf=Ro)以及內導體處出射的單邊碰撞ξii(rs=Ri且rf=Ri)四種不同的類型.

另外,上述推導可以使用參數ηi來衡量電子軌跡表達式的計算精度,其中ηi等于ηs(rs=Ri).為確定近似軌跡表達式的適用范圍,下面分別使用電子軌跡表達式((2)式)與四階龍格-庫塔方法計算不同參數條件下的電子運動軌跡.為便于區別,下面將這兩種方法得到的電子軌跡分別簡稱作解析軌跡與數值軌跡.由于龍格-庫塔方法的求解精度非常高,所以數值軌跡可以作為真實的電子軌跡進行參考比較.圖2給出了不同ηi值下四種軌跡類型的解析軌跡與數值軌跡,其橫坐標與縱坐標分別為電子的相位變化量?φ與歸一化的電子運動位置?ξ.可以看到,在ηi=10時,電子運動過程中的快速振蕩幅度遠小于緩慢漂移的幅度,電子的解析軌跡與數值軌跡符合得很好;但隨著ηi的減小,快速振蕩運動變得越來越劇烈,電子的碰撞也逐漸變得由快速振蕩運動所主導,同時微擾法的成立條件也逐漸失效,解析軌跡與數值軌跡之間的偏差也越來越大;在ηi=3時,電子在渡越過程中的軌跡偏差已經較為明顯,但碰撞發生時,兩種方法計算的電子渡越時間偏差仍可以接受;而當ηi減小至1.25時,兩種軌跡之間已經表現出非常大的偏差.綜上所述,只有滿足ηi>3條件,近似的電子軌跡表達式才具有可接受的精度,同時后面統計理論的穩態建模也不會在計算微放電閾值時產生較大的誤差.

圖2 不同ηi值下不同類型解析軌跡與數值軌跡的對比Fig.2.Comparison of analytical and numerical trajectories for different ηi.

從本質上看,電子的出射隨機性是造成上述電子運動軌跡差異的重要因素.假設電子的出射速度u滿足如下麥克斯韋分布:

式中υt表示平均出射速度,可以通過平均出射動能Et(通常取1.5 eV)計算得到.基于上述推導的軌跡表達式,同軸結構微放電中的聯合概率密度函數G(τ|φs;ξ)則可以寫為

與平行平板微放電中一樣,其在物理意義上同樣表示以相位φs出射的電子在經歷渡越時間τ后以軌跡ξ(ηs,ηf)發生碰撞的概率密度.上式中u=g(τ|φs;ξ),只是假定的表達式. 從(2)式中可以看到,電子軌跡的解析表達式過于復雜,因而無法由其轉換得到u關于τ的顯式表達式.因此,這里引入一種基于隱式關聯性的聯合概率密度函數構建方法,用于求解同軸結構微放電中電子渡越時間的概率分布.在實際計算過程中,任意給定的渡越時間τ所對應的出射速度u可以通過電子軌跡的表達式數值求解得到,(5)式右邊的求導項則可以改寫為如下隱式形式:

需要注意的是,上式求解過程應當篩選掉單個出射速度u對應多個渡越時間τ的情況,其本質上是電子的快速振蕩運動在邊界處發生的非物理碰撞.

2.2 統計理論穩態建模

結合上述聯合概率密度函數,本節通過推導內、外導體處電子出射相位分布所滿足的積分方程組,構建同軸結構微放電統計理論的穩態模型.為便于理解,方程推導從電子數目與出射相位分布隨電子更新換代的變化過程出發,同時考慮同軸結構微放電的非對稱性.假設微放電過程中經歷過相同碰撞次數所產生的二次電子為同代電子,內、外導體處第l?1代電子的數目分別表示為和,而相應的出射相位分布函數為和.這些電子碰撞后產生第l代二次電子的數目和將分別滿足

與

與

其中K函數寫為

式中θ(τ|φs)為階躍函數,而σ(τ|φs;ξ)為材料的二次電子發射系數(SEY)函數,它是通過電子軌跡表達式的導數求解電子碰撞動能,再結合描述SEY分布的唯象模型構建得到.此外,(9)式與(10)式右邊的第一項和第二項分別代表單邊和雙邊碰撞所產生的二次電子發射,由于雙邊碰撞產生二次電子的出射方向發生了變化,所以相鄰兩代電子的出射相位分布之間需要引入半個周期的相位偏移.

從本質上看,場分布的非均勻性使得同軸結構中形成非對稱的微放電過程,而內、外導體處的電子出射相位也會形成不同的穩態分布,所以平行平板微放電穩態建模中將其處理為第二類Fredholm積分方程的方法就不再適用.早前的研究[22]雖然基于這種求解方法實現了近似的穩態建模,但由于忽略了同軸結構微放電過程的非對稱性,其最終得到的微放電閾值計算精度也會受到影響.鑒于此,這里為上述穩態積分方程組引入如下聯立迭代求解方法.首先,假設內、外導體處初始(首代)電子的數目分別為和,它們的出射相位分布和都是均勻的,將這些參數代入(9)與(10)式后,即可分別求得內、外導體處首代二次電子的數目與出射相位分布;繼續迭代求解后續代數電子的相應參數,直至內、外導體處電子出射相位分布趨于穩定.在實際的迭代求解過程中,當內、外導體處相鄰兩代電子出射相位分布的總相位偏移率不超過10?4時,即可判定同軸結構中的微放電過程已經發展至穩態.

圖3(a)和圖3(b)中分別給出了同軸結構發生微放電時內導體與外導體處電子出射相位分布與相鄰兩代電子數目比值隨電子代數更迭的變化情況,其中f=1.6 GHz與Vrf=280 V.可以看到,同軸結構中的微放電過程中發生了明顯的相位聚焦現象.隨著電子碰撞發生,內、外導體處的電子出射相位分布迅速朝有利區間[?π/4,π/2]聚攏并最終達到穩定,同時相鄰兩代電子數目的比值在經歷初始振蕩后也很快趨于恒定.另外,內、外導體處電子出射相位的穩態分布并不相同,由于內導體處的電場強度要高于外導體處,所以內導體處的相位聚焦效果更強.同時,上述方程組求解只進行了數次(十次以內)迭代后,內、外導體處電子的出射相位分布就已經達到穩態.因此,同軸結構微放電的穩態建模采用這種聯立迭代方法可以快速確定電子數目的變化趨勢.

此外,圖4還給出了不發生微放電(Vrf=200 V)、臨界微放電(Vrf=245 V)以及發生微放電(Vrf=280 V)三種不同情況下同軸結構內導體與外導體處電子出射相位的穩態分布.觀察發現,微波場電壓的升高使得電子出射相位分布更加集中.因為在強電場的作用下,以有利相位出射的電子可以得到更多的動能,并碰撞產生更多二次電子,而以非有利相位出射的電子則更多地被“淘汰”掉,從而產生更顯著的相位聚焦效應.同時,相比于內導體處電子出射相位分布的微弱變化,外導體處電子出射相位分布的變化更為明顯,這也間接說明外導體處的電子碰撞情況主導著同軸結構微放電的整體發展趨勢,這與非穩態建模的分析結果一致.

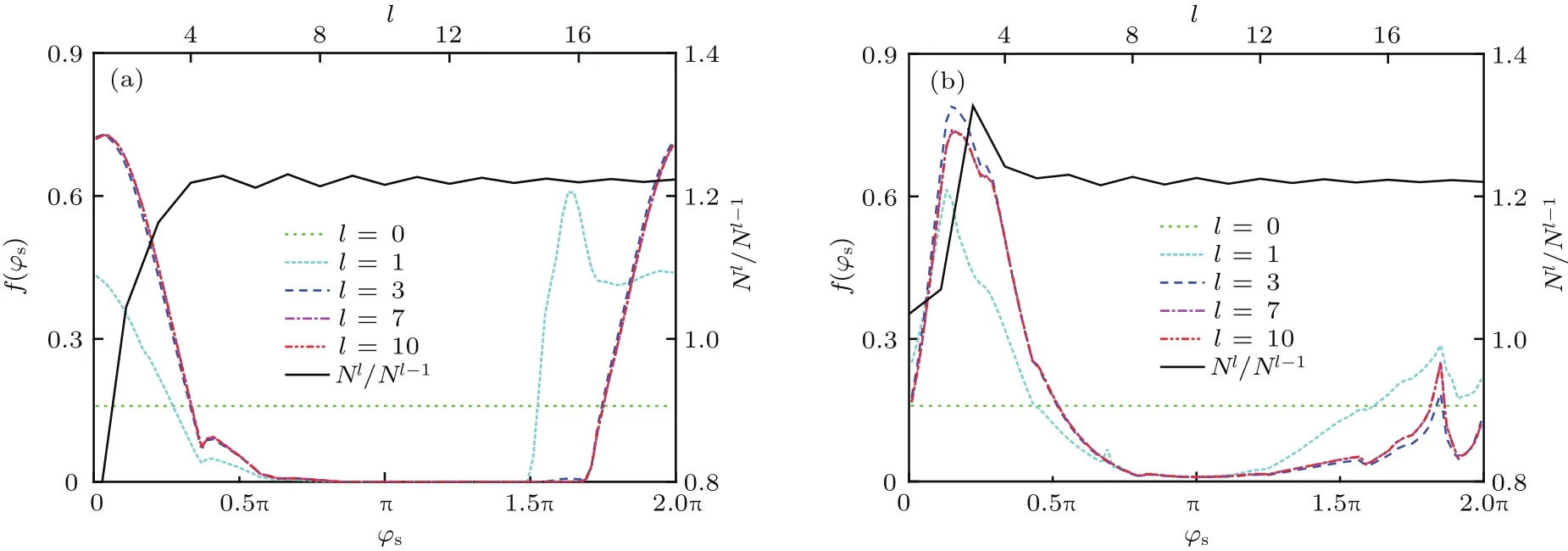
圖3 同軸結構內導體(a)與外導體(b)處電子出射相位分布與相鄰兩代電子數目比值隨電子代數更迭的變化情況Fig.3.Convergence of electron emission phase distribution and electron population ratio at the inner conductor(a)and outer conductor(b)of coaxial geometry along with iteration process.

圖4 不同微放電情況下同軸結構中內導體(a)與外導體(b)處電子出射相位的穩態分布Fig.4.Steady distribution of electron emission phase at the inner conductor(a)and outer conductor(b)of the coaxial geometry along with the iteration process.

最后,為準確判定微放電的閾值電壓,統計理論穩態建模通過微放電趨于穩態時相鄰兩代電子數目的比值計算下面的有效二次電子倍增率σeff,以此表征微放電的發生程度.上標“st”表示微放電達到穩態,而根據σeff的大小就可以判斷是否會發生微放電.當σeff>1時,微放電過程中的總電子數目呈指數倍增,明顯會發生微放電;σeff<1則表示總電子數目隨碰撞的發生而逐漸減少,因而不發生微放電;而σeff=1則對應于發生微放電的臨界情況,此時的微波場電壓即為微放電的閾值電壓.

3 同軸傳輸線的敏感區域計算與分析

結合2.1節中構建的聯合概率密度函數,再根據2.2節中推導的解析穩態方程及引入的聯立迭代求解方法,就可以計算不同參數條件下的有效二次電子倍增率,由此計算得到同軸結構微放電的敏感區域,進而實現器件結構與材料對微放電閾值影響的規律分析.為此,本節采用上述穩態模型分別計算銀、銅、鋁與阿洛丁等工程常用鍍膜材料[25]的同軸傳輸線微放電敏感區域,各材料的結果具體如圖5—圖8所示.另外需要強調的是,上述敏感區域計算統一采用默認尺寸的同軸傳輸線,而且這些材料的SEY分布也都采用修正的Vaughan模型[26]擬合,具體如下面的分段公式所示.

另外,圖5—圖8中還給出了ESA通過實驗測量得到的相同材料同軸傳輸線的微放電閾值結果,以便于進一步的對比與分析.由于穩態建模采用的是近似的電子軌跡表達式,其誤差會影響到微放電閾值的計算精度,而ηi作為電子軌跡表達式精度的衡量因子,其數值越高,電子軌跡的計算誤差越小,所預測的微放電閾值也越精確.如前所述,近似的電子軌跡表達式只有在ηi>3.0時才有可接受的精度,因此下面分析中將滿足該條件的右下方敏感區域當作可信區域,而圖中的黑色虛線正好對應由ηi=3.0條件決定的可信區域邊界.

表1 不同材料SEY的Vaughan模型擬合參數Table 1.Fitting parameters of Vaughan model for different material’s SEY.

圖5 銀材料鍍膜同軸傳輸線的微放電敏感區域Fig.5.Multipactor suscepbility zone of coaxial transmission lines for silver coating.

可以看到,材料SEY特性的差異使得上述材料的微放電敏感區域之間表現出明顯的不同.相對而言,銀、鋁與銅材料由于具有較高的σm值與較低的E1值,更容易產生二次電子發射,從而形成更大的微放電敏感區域,而右下方的敏感區域也更多地進入可信區域內,所以由穩態模型計算的微放電閾值與實驗結果之間也符合得更好.然而,SEY整體分布較低的阿洛丁則表現出相對較高的微放電閾值,尤其在一階敏感區域處.由于左側三個頻點處敏感區域的邊界明顯超出可信區域,因此微放電閾值的預測結果也表現出較大的誤差,但對于高階敏感區域而言,由穩態模型計算的微放電閾值在大多數頻點處與實驗結果則符合得很好.

圖6 鋁材料鍍膜同軸傳輸線的微放電敏感區域Fig.6.Multipactor suscepbility zone of coaxial transmission lines for aluminium coating.

另外,非穩態模型雖然也可以實現同軸結構微放電的機理分析與閾值預測,但同軸結構中的電子在米勒力作用下更可能發生長程單邊碰撞,因此非穩態建模需要耗費更多的計算時間模擬微放電的實時演化過程.而穩態建模可以基于聯立迭代方法直接求解上述穩態方程組,從而實現同軸結構微放電閾值與敏感區域的快速計算.對比發現,使用非穩態模型求解各實驗頻點處微放電閾值的計算耗時約是使用穩態模型的3—5倍,因此穩態建模也為后面微放電敏感區域的對比分析提供了高效實用的計算工具.

同時,為分析平行平板與同軸結構微放電的閾值差異,上述敏感區域圖中還給出了不同材料的平行平板微放電敏感曲線(σeff=1),即敏感區域的邊界,而平行平板的微放電統計理論建模及敏感區域計算方法參見文獻[21].對比發現,平行平板微放電的一階與三階敏感區域相互分離,但與其相比,同軸結構微放電的敏感區域則較為集中,尤其三階敏感區域相對向左偏移,并與一階敏感區域出現明顯的交疊,這與早期Woo[27]在同軸結構微放電實驗中得到的閾值規律相符合.

圖7 銅材料鍍膜同軸傳輸線的微放電敏感區域Fig.7.Multipactor sensitivity zone of coaxial transmission lines for copper coating.

圖8 阿洛丁鍍膜同軸傳輸線的微放電敏感區域Fig.8.Multipactor suscepbility zone of coaxial transmission lines for alodine coating.

此外,中間幾階敏感區域的下邊界也不像平板微放電中那樣平滑,并表現出較大波動,這使得兩種結構微放電閾值的相對大小交替變化.可以看到,三階敏感區域左側的同軸結構微放電閾值要小于平行平板微放電閾值,但其右側處卻表現出相反的規律.同時在高階敏感區域處,兩種結構的微放電閾值差異情況對于不同材料也是不一樣的.對于銀、銅與鋁材料而言,平行平板與同軸結構的微放電閾值在高階敏感區域處較為一致,但阿洛丁中的閾值差異則較為顯著.

為分析SEY參數對微放電敏感區域大小的影響,圖9繪制了上述鍍膜材料的同軸傳輸線微放電敏感曲線.可以看到,這些材料的微放電閾值大小順序為Cu

圖9 不同鍍膜材料的同軸傳輸線微放電敏感曲線對比Fig.9.Comparison of multipactor suscepbility curves of coaxial transmission lines for different coating materials.

圖10分別給出了1.15,1.6與3.0 GHz三個不同頻率下微放電閾值電壓與功率隨同軸結構徑比γ的變化曲線.為準確分析徑比變化對微放電閾值的影響,我們在改變同軸結構徑比時保持其內徑與外徑之間的差值不變,即d恒等于2.01 mm.另外要說明的是,本文的統計理論建模基于近似推導的電子軌跡表達式,其在計算高徑比的同軸傳輸線微放電閾值時具有較大的誤差,因此這里只分析了[1.2,4.2]范圍內的徑比變化對同軸傳輸線微放電閾值的影響規律.可以看到,在徑比小于2.5時,同軸傳輸線的微放電閾值電壓會隨著徑比的增加而緩慢降低,但由于其特征阻抗也隨之升高,同軸傳輸線中發生微放電的閾值功率隨之迅速減小.然而當徑比增加到一定數值(2.7—3.5之間)時,微放電閾值電壓會發生驟增現象.這是因為同軸結構徑比的變化使得不同階數的微放電敏感區域發生相對偏移,而當這種偏移使得計算頻點從高階敏感區域進入低階敏感區域時,相應頻點處的微放電閾值電壓就會突然上升.另外,當徑比位于該范圍的中間段時,同軸傳輸線的微放電閾值電壓與功率會出現最小值,而且不同頻點下對應于微放電閾值最小值的徑比值也不相同.由此可見,同軸微波器件的設計優化必須考慮其在工程應用中的實際工作頻率,并通過擇優選取合適徑比值來獲得相對更高的微放電閾值.

圖10 不同頻點下同軸傳輸線微放電閾值電壓與功率隨徑比的變化Fig.10.Effect of the radius ratio of coaxial transmission lines on multipactor threshold voltage and power for different frequency points.

4 討 論

本文通過同時考慮單邊碰撞和雙邊碰撞的統計理論穩態建模實現了同軸結構微放電的敏感區域計算以及器件結構與材料對微放電閾值的影響分析.事實上,考慮矩形波導中橫向非均勻場分布的影響,這種改進穩態建模方法同樣可以推廣到矩形結構微放電研究中,由此解決現有穩態模型無法考慮單邊碰撞而造成閾值精度低的問題.此外,改進后的穩態模型還可以進一步推廣應用到其他非對稱的微放電過程分析中,例如外加垂直靜電場作用下平行平板結構以及介質填充平行平板與矩形波導中的微放電研究.

另外,上述研究還表明電子的快速振蕩振幅會隨著ηi的減小而逐漸增強,而緩慢漂移對整體電子軌跡的影響則會隨之變弱.ηi<3.0參數范圍內幾乎可以忽略同軸結構中場分布的非均勻性,并用具有均勻場分布的平行平板結構來等效,因而兩種結構微放電的敏感區域在左上方處應較為相似,但上述敏感區域圖中卻表現出非常顯著的差異,而這主要是不精確的電子軌跡表達式所造成的.對于低SEY的鍍膜材料而言,軌跡誤差甚至會影響到右下方敏感區域處的閾值計算精度.然而同軸結構中無法推導得到精確的電子軌跡表達式,要解決近似電子軌跡表達式帶來的計算誤差問題,就必須在采用數值方法計算電子軌跡的基礎上實現統計理論建模,而這也是未來統計理論發展與應用亟待解決的難題.

5 結 論

為實現精確有效的同軸傳輸線微放電閾值分析,本文采用由微擾法近似推導同軸結構的電子軌跡表達式,提出基于隱式關聯性的聯合概率密度函數構建方法,并在考慮單邊與雙邊碰撞對微放電影響的情況下,推導同軸結構內、外導體處電子出射相位分布所滿足的穩態積分方程組,由此實現了同軸結構微放電統計理論的穩態建模與分析.然后,采用該穩態模型分別計算銀、鋁、銅與阿洛丁等工程常用鍍膜材料的同軸傳輸線微放電敏感區域.與歐空局的實驗結果對比表明,近似電子軌跡表達式的誤差在右下方的敏感區域(滿足ηi<3條件)處可以忽略,因此穩態模型可以準確預測同軸傳輸線的微放電閾值.而具有低SEY分布的阿洛丁鍍膜具有相對較小的敏感區域及較高的微放電閾值,是工程實際中實現微放電抑制的有效鍍膜選擇.另外與平行平板微放電相比,同軸結構微放電的敏感區域較為集中,尤其一階與三階敏感區域會發生明顯的交疊,同時兩種結構微放電閾值的相對大小在中間幾階敏感區域邊界處交替變化.最后分析同軸結構徑比對微放電閾值的影響規律發現,不同頻率的同軸傳輸線微放電閾值功率在特定徑比下會達到最小,實際的微波器件設計中須盡可能地避免采用該徑比值,才能獲得相對更高的微放電閾值功率.