基于勢流理論的回轉體并聯入水雙空泡演化動力學研究?

宋武超 魏英杰 路麗睿 王聰 盧佳興

(哈爾濱工業大學航天學院,哈爾濱 150001)

(2018年7月17日收到;2018年9月11日收到修改稿)

1 引 言

運動體以一定的速度撞擊自由液面,將自身動能傳遞給了附近水域,引起流體質點向運動體外側運動,致使空泡敞開及自由液面噴濺,形成入水空泡.作為典型跨界質過程的入水過程,涉及運動體、空氣和水三者的耦合作用,具有高度非線性和非定常性,運動體的運動特性和流場特性都極為復雜.

早在19世紀末,Worthinghton和Cole[1,2]利用閃光攝影技術對球體等垂直入水時產生的入水空泡進行了大量的試驗研究,并對入水空泡流動現象做了開創性的描述.二戰以后,在美國海軍支持下,學者們針對入水過程開展了系統性的試驗研究工作,其中代表性的有Waugh[3],Birkho ff和Caywood[4],Glibarg和Anderson[5]以及May和Woodhull[6]等.21世紀以來,隨著試驗設備、測量技術的革新,從運動體入水過程的試驗中獲得的信息更加全面,為入水空泡流體特性的研究提供了更加有效的方法和途徑[7].Holfeld等[8]和Tabuteau等[9]分別在微重力、不同黏度液體等特殊條件下開展了入水實驗研究.對于入水空泡形態預測的理論方法,Logvinovich[10]首次提出了基于能量守恒定律的空泡獨立膨脹原理,為之后空泡發展理論研究提供了重要基礎.Lee等[11,12]基于能量守恒定律,提出了描述高速入水空泡形態發展演化的理論方法,對入水空泡擴展、收縮和閉合過程進行了較為精確的描述.Truscott[13]將Logvinovich提出的獨立膨脹原理進行了擴展,準確地預測了運動體傾斜入水過程中入水空泡形體的演化規律.Yan等[14]基于勢流理論建立了低速入水空泡動力學模型.Gordillo等[15]采用勢流理論推導了高雷諾數入水條件下空泡閉合點流動特征.Aristo ff和Bush[16]同樣基于勢流理論得到了入水空泡形態的理論解.國內方面,葉取源[17]基于歐拉-拉格朗日混合邊界元法,求解獲得了圓錐垂直入水過程中入水空泡形成、發展以及閉合的變化規律.路中磊[18]基于Yan等[14]的分析方法,建立了適用于開放空腔入水空泡波動預測的理論模型.張阿漫等[19]基于勢流理論分析了氣槍氣泡遠場壓力子波特性.

在現有關于入水空泡動力的研究中,多以單個運動體入水所形成入水空泡的動力學特性作為研究重點,主要考慮了空泡的演化過程,并對其流動方式進行了簡化,形成了較為完善的單獨低速軸對稱入水空泡動力學計算模型.然而,對于雙運動體入水過程所形成的入水空泡的動力特性,尚無人涉及.雙回轉體入水過程中所形成的入水空泡,呈現出了較強的非對稱性;兩回轉體軸線內側區域空泡演化過程中,流體形成了相對流動,從而使得流動不再具有軸對稱特性,而發展成復雜的三維流動,且具有強非線性,使得理論模型的建立難度更大.

本文首先簡要介紹單獨入水空泡與并聯入水空泡各自的演化特性;而后基于勢流理論,在現有的單獨入水二維軸對稱計算模型的基礎上,將并聯入水過程中空泡之間的擾動簡化為擾動速度勢,給出擾動最強區域的空泡演化擾動模型;基于非線性假設,引入三維影響函數,通過影響函數建立空泡自由擴張區與擾動擴張區的過渡關系,得到三維非對稱空泡演化計算模型,并基于該模型分析同步并聯入水過程空泡形態的三維演化特性.

2 單獨入水空泡與并聯入空泡演化特性分析

2.1 實驗系統與模型參數

試驗系統由試驗水槽、光學測試系統和釋放機構三部分組成,如圖1所示.試驗水槽采用尺寸為300 mm×300 mm×900 mm的小型水槽,水槽四壁為鋼化玻璃,壁厚10 mm,槽底墊有緩沖橡膠墊,防止射彈入水對缸體造成破壞.試驗光源采用4盞發光二極管(LED)作為背景光,并用柔光屏對背景光進行柔化,使背景光均勻撒布,以達到良好的拍照效果;采用2盞LED燈作為頂光,以增強空泡內部光照條件,進而增強圓柱體邊界清晰度,便于圖片數據的后期處理.圓柱體運動過程通過Photron FASTCAM SA-X型高速攝像機采集,并通過自編程序對運動軌跡及運動姿態進行提取,以獲得圓柱體運動特性.相機采集幀率為2000 fps,相機上安裝廣角鏡頭,以擴大視野,捕捉更多運動信息.

釋放機構由推拉式電磁鐵和豎直導軌組成,如圖2所示.其中豎直導軌起導向作用,以確保試驗模型入水時保持豎直姿態;推拉式電磁鐵通過觸發開關控制,共用同一個電信號,以確保觸發的同步性.當電源接通時,電磁鐵推拉桿同時收縮,釋放模型.為防止電磁鐵收縮引起的支架振動對釋放產生影響,導軌和電磁鐵分別安裝在不同的支架上,導軌支架和電磁鐵支架相互獨立.

試驗模型如圖3所示.模型直徑D=10 mm,長L=60 mm,模型采用6063鋁合金加工,密度為2.7 g/cm3.

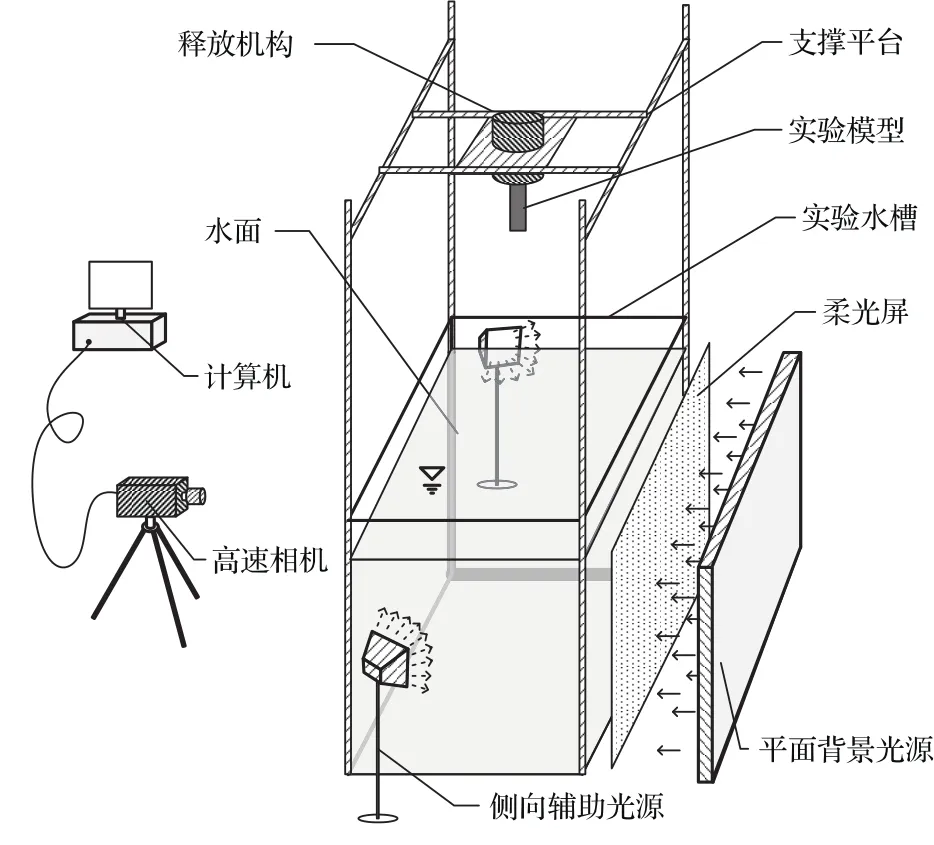
圖1 試驗系統示意圖Fig.1.Experiment system of water-entry.

圖2 釋放機構示意圖Fig.2.The mechanism to release the model.

圖3 模型尺寸Fig.3.Sketch of water-entry model.

2.2 實驗結果分析

圖4(a)給出了回轉體單獨入水空泡形態時歷演化過程.回轉體在入水過程中經歷了入水撞擊(t=0 ms)、開空泡(t=10—30 ms)、空泡閉合(t=10—50 ms)、空泡隨動及空泡潰滅(t=60—80 ms)等五個階段.在入水撞擊階段,回轉體通過入水沖擊將其自身動能傳遞給附近水流體,水流體形成向外排開運動,入水空泡形成;在開空泡階段,回轉體通過阻力作用不斷將動能傳遞給附近水流體,致使回轉體底面邊緣處形成持續的流動分離,在宏觀上表現為空泡敞開(t=10—30 ms);在空泡閉合階段,氣水界面處流體質點在運動過程中受到壓力與表面張力的作用,做減速運動,當速度減小為0時開始反向加速,使得空泡形成“頸縮”現象,空泡發生閉合(t=40—50 ms);空泡完成閉合后,回轉體底面仍不斷形成流動分離,分離所形成的空腔需要空氣進行填充,使得封閉在空泡內部的氣體隨著分離所形成的空腔位置的變化而流動,空泡形成隨動(t=60—80 ms);在隨動空泡形成后,閉合點處空泡內外存在壓力梯度,使得水流體沿回轉體壁面向泡內流動,形成回射流,空泡界面受回射流撞擊而逐漸云化潰滅.

圖4(b)給出了回轉體同步并聯入水空泡形態.對比單獨入水空泡形態與并聯入水空泡形態可以看出,單個回轉體擾動下,流場流動具有軸對稱性,因而空泡形態表現出良好的軸對稱特征;在同步并聯入水過程中,兩空泡在回轉體軸線內側區域形成擾動,單空泡形態演化呈現出明顯的不對稱特征.在開空泡階段,空泡向兩回轉體軸線中間區域的擴張受到了限制,以致兩回轉體外側空泡半徑明顯大于內側,中間區域形成的噴濺高度亦較外側高;在空泡閉合階段,兩回轉體軸線外側區域空泡界面率先收縮,空泡閉合點偏向兩回轉體軸線內側,且閉合時間變晚.在空泡隨動階段,隨動空泡亦呈現出不對稱特征.總之,在整個入水過程中,單獨入水空泡始終保持很強的軸對稱特性,而并聯入水空泡則始終呈現較強的鏡面對稱特征.

圖4 單獨入水與并聯入水空泡演化對比(V0=1.9 m/s) (a)單獨入水空泡;(b)同步并聯入水空泡Fig.4.Comparison of parallel water-entry cavities and single water-entry cavities:(a)Single water-entry cavities;(b)parallel water-entry cavities.

結合圖5對空泡形態不對稱原因解釋如下:在開空泡階段,外側空泡自由擴張,而內側空泡的發展受到了相鄰圓柱體的影響.空泡在兩圓柱體中間區域擴張時,空泡邊界附近流體形成了對流,流體質點間動能傳遞受到限制而轉變成流場勢能,致使中間區域噴濺高度增加而空泡半徑減小,空泡形態呈現出不對稱特性.同時,由于中間區域較少的流體獲得了來自兩個圓柱體的動能,流動速度較外側區域大,致使該區域流場壓力低于外側空泡界面附近的流場壓力,導致在空泡閉合階段,外側空泡界面在較大壓力作用下率先收縮,且收縮速率大于內側空泡界面,最終使得閉合點偏向兩圓柱體軸線內側.

圖5 并聯入水空泡流動示意圖Fig.5.The flow schematic of water entry cavity.

3 單獨入水過程動力學方程

3.1 單獨入水過程初邊值分析

分析可知,在單獨入水過程中入水空泡形態始終保持軸對稱特性,因此空泡演化動力學模型建立在如圖6所示的柱坐標系下.柱坐標原點取在回轉體軸線與自由液面的交點處,r軸取回轉體徑向,z軸取回轉體軸線,其正方向指向回轉體運動方向.

圖6 回轉體單獨入水空泡示意圖Fig.6.Schematic of single water-entry cavity.

對于單獨回轉體入水過程,可假設流體處于無旋狀態.因此,流場的速度可以用速度勢函數?(r,z,t)進行描述,速度勢?(r,z,t)在流域內滿足Laplace方程:

此時,流域內的速度分布可以用下式表示:

在自由液面處SF(r,t)處,速度勢滿足歐拉方程:

其中ps為自由液面處的壓力,ρ為液體密度.在空泡閉合前,該壓力恒等于大氣壓.在回轉體表面,速度勢滿足物面條件:

式中,v為回轉體運動速度,n=(nz,nr).速度勢在遠場滿足遠場邊界條件:

在初始時刻,運動體僅僅觸碰到了自由液面,此時,自由液面尚處于靜止狀態,初始速度勢滿足如下初始條件:

3.2 回轉體動力學方程及空泡演化方程

在回轉體過程中,其動力學方程可表達如下:

式中M為回轉體質量,F(t)為回轉體受到的流體動力.回轉體在入水過程中,僅頭部沾濕,因此流體動力可視為回轉體頭部所受到的流體壓力.該流體壓力由動壓和靜壓兩部分組成,其表達式為

式中,pw為回轉體頭部沾濕面上受到的壓力,其滿足伯努利方程:

將(8)和(9)式代入(7)式得到回轉體單獨入水過程的動力學方程如下:

式中,Ab為回轉體底部面積,Ab=πR2,R為底部圓形面半徑;lc為空泡長度,其滿足

對空泡進行細長體假設[20],即dr/lc=ε?o(1),其中dr為空泡直徑,此時,在空泡壁面附近的流動可以假設為二維流動:

此時,(1)式可簡化為

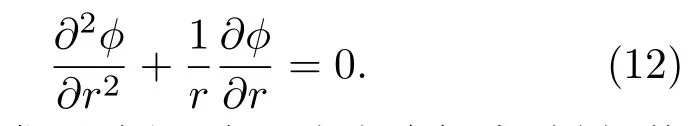
對于空泡發展過程,在入水空泡初生時刻,其半徑等于回轉體半徑.因此入水空泡半徑演化的隱式方程:

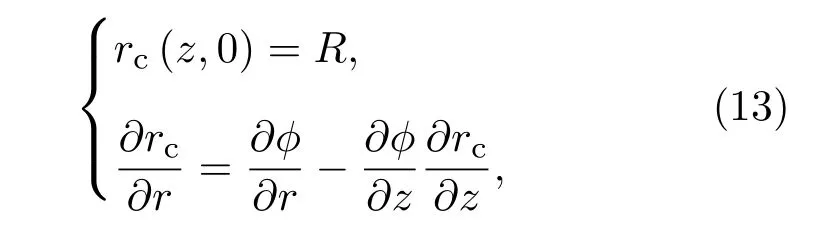
其中,rc為空泡直徑.

3.3 速度勢分析

基于建立的入水空泡半徑演化方程(13)可知,若給出速度勢?(r,z,t),則可得到入水空泡半徑的演化規律,因此本節基于漸進理論對速度勢函數?(r,z,t)進行分析.

為了描述空泡界面的運動,入水過程的速度勢可以看作由一個位于回轉體底面中心處的點源?b和一個位于空泡軸線處的線源?c組成:

空泡形成擴張的速度主要來源于回轉體底部的空泡分離點.因此,空泡的擴張運動主要受三維點源?b的作用[14]:

上式第二項對空泡演化的作用為抑制作用,由于對空泡進行了細長假設[20],則(16)式的第二項為一小量,因此可忽略.根據文獻[14],點源強度由下式給出:

式中,C1為修正系數,文獻中給出的C1=2.78,本文經過與試驗結果對比,將其修正為2.76,得出點源速度勢為

空泡的收縮主要受空泡軸線上分布的線源影響,其在某一空泡界面上具有二維作用效果,在整個空泡域,又具有三維作用效果.因此,空泡收縮的線源速度勢可表示為

文獻[14]中給出了線源的強度表達式,由此可以確定總速度勢:

3.4 計算模型求解

將速度勢代入(10)式得到回轉體單獨入水過程的完整動力學方程,并采用經典四階龍格-庫塔法對其進行數值求解.在求解過程中,時間步長取?t=0.0001 s,在z方向(入水方向,如圖2所示)的離散取?z=0.001 m.圖7給出了求解所得z方向位移隨時間的變化與試驗結果的對比,從圖中可以看出,計算結果與試驗結果符合良好.

圖7 位移結果對比(V0=1.9 m/s)Fig.7.Comparison of theory model calculative results and experimental results.

圖8給出了入水空泡形態計算結果與試驗結果的對比.從圖中可以看出,整體上看計算結果與試驗結果符合度較好,證明了該理論模型計算結果的正確性.在靠近自由液面處,計算模型結果較試驗結果差別較大,這是由于計算模型中忽略了自由液面處的非線性噴濺流動,但并不影響入水空泡整體形態預測.

圖8 入水空泡形態計算結果與試驗結果對比(V0=1.9 m/s)Fig.8.Comparison of water-entry cavities of calculative and experimental results(V0=1.9 m/s).

4 同步并聯入水過程雙空泡演化擾動模型

4.1 動力學建模簡化方法

在回轉體同步并聯入水過程中,回轉體空泡外側的發展呈自由擴張狀態,內側發展受到來自相鄰空泡的干擾,而呈現出受迫演化狀態.由第2節對并聯入水空泡演化試驗結果的分析,發現空泡在空間上呈對稱特性,因此可將內側區域空泡演化對稱面作為擾動勢對內側空泡的發展演化進行分析.該擾動勢的作用范圍為?,如圖9所示.

圖9 對稱面擾動勢作用示意圖Fig.9.Schematic of symmetry plane disturbance potential.

引入對稱面處的擾動勢,將入水空泡的演化通過二維軸對稱的方法進行分析,其在三維空間中相當于引入了一個柱面約束,空泡在該柱面約束下進行軸對稱受迫發展,如圖10所示,該約束柱面可稱為有勢壁面.

圖10 二維軸對稱模型有勢壁面約束本質示意圖Fig.10.Schematic of potential wall constraint of the planar axisymmetrical model.

4.2 有勢壁面速度勢分析

由第2節體并聯入水空泡演化特性分析可知,回轉體入水過程約束勢?s可認為由兩部分組成,一部分是對擴張的約束,另一部分是對收縮的約束.結合3.3節關于速度勢分析可知,空泡的擴張主要受位于回轉體底部中心處的點源速度勢?b的影響,而空泡的收縮主要受位于空泡軸線處的線源速度勢?c作用.因此,對于空泡擴張與收縮的抑制,我們同樣引入一個隨回轉體底部中心運動的點匯?b,s和位于空泡軸線處的線源?c,s.有勢壁面的速度勢則可以表示如下:

對于?b,s的分析,根據勢流疊加原理,通過分析?b,s與?b的合速度勢?b,sum來給出?b,s,?b,sum可由下式表示:

合速度勢?b,sum可用三維點匯表示:

其點匯強度σsum(t)與擾動勢無量綱作用范圍??(??=?/R)呈負相關,且根據試驗結果,隨著入水時間的增加,空泡最大直徑減小,內外側空泡直徑差異減小,表明其對空泡擴展的約束與時間呈負相關.

根據有勢壁面的不可穿越性,合速度勢需要滿足如下邊界條件:

其中,tp為空泡的無量綱閉合時間,tp=Tv/R,T為空泡閉合時間,可按照文獻[21]給出的經驗公式求得:根據試驗修正給出.(24)式給出了滿足上述條件的點匯強度:

其中C1=2.76.

將(24)式代入(26)式得到合速度勢為

根據勢流疊加原理推得有勢壁面的點匯如下:

線源?c,s可以通過在r=2?處引入一個相同強度的線源進行表示,其源強度由(19)式給出,得到?c,s如下:

4.3 計算模型驗證

速度勢代入回轉體動力學方程,采用經典四階龍格-庫塔法求解,得到在有勢壁面影響下的位移,并將其與單獨入水位移和試驗結果進行比較,如圖11所示.從圖中可以看出,有勢壁面對回轉體z方向的位移影響很小.

圖11 位移結果對比(V0=1.9 m/s)Fig.11.Comparison of displacement results.

圖12 計算結果與試驗結果對比(V0=1.9 m/s)Fig.12.Comparison of water-entry cavities of calculative and experimental results.

基于第3.4節中對回轉體位移的求解結果,開展在有勢壁面約束下的空泡半徑演化計算,在z方向的離散取?z=0.001 m,圖12給出了有勢壁面約束下,空泡半徑與試驗工況下兩回轉體軸線內側空泡半徑的對比.從圖中可以看出,理論結果與試驗結果符合度較好,證明了該擾動模型的正確性.

5 三維空泡形態演化模型

5.1 非線性影響函數建立

由4.1節分析可知,在空泡的演化中,空泡沿回轉體的徑向擴張,對稱面對空泡的影響區域如圖13所示,白色區域空泡均呈現自由擴張,僅在灰色區域空泡會受到對稱面的影響.

圖13 對稱面對空泡演化的影響區域Fig.13.Schematic of the influence region of symmetry plane on the cavity evolution.

基于上述的影響區域,我們將柱坐標系下的柱面有勢壁面展開為笛卡爾直角坐標系下的有勢平面,其對空泡的影響通過影響函數β來確定,其原理示意如圖14所示.

設空泡的實際半徑為rc,在有勢壁面完全影響下的空泡半徑為rc1,自由擴張半徑為rc2,則其三者的關系可用下式表示:

其中,β為影響函數,其具體形式如下文所述.

圖14 有勢壁面展開示意圖Fig.14.Schematic of the potential wall expansion.

以有勢壁面完全影響下的空泡邊界與展開后的有勢壁面之間的距離作為影響函數權重,在如圖15所示的極坐標系下進行推導,其中l1為有勢壁面,l2為有勢壁面完全約束下的空泡半徑,r1為回轉體中心到圓柱有勢壁面的距離,r2為回轉體中心距離展開后的有勢壁面的徑向距離.

圖15 極坐標系Fig.15.Polar coordinate system.

(29)和(30)式給出了l1和l2在極坐標系下的曲線方程:

兩條曲線間的距離如下:

圖15中,i為有勢壁面的法向,對空泡壁面的影響其主要作用的分量為空泡邊界的法向分量in,因此,影響函數的非線性假設如下:

其中,k,b和q均為未知參數.

上式需要滿足邊界條件:

此外,在θ=π/2處,即未受影響區域和受影響區域交界處,空泡截面邊界應滿足連續可導條件.在笛卡爾坐標系下,取1/2空泡截面,未受影響區域,空泡截面為一1/4圓,其在x=0處?y/?x為0,因此受影響區域在該處也應滿足:

其中

得到影響函數β的表達式如下:

5.2 計算結果驗證

基于5.1節中對影響函數的推導,對基于影響函數的三維空泡演化理論模型進行驗證.圖16給出了基于影響函數的空泡同步并聯入水三維空泡形態計算結果及其與試驗結果的對比.從圖中可以看出,計算結果與試驗結果符合較好,說明了該空泡演化模型的正確性.

圖16 三維空泡理論結果與試驗結果對比 (a)t=0.01 s;(b)t=0.02 s;(c)t=0.03 s;(d)t=0.04 s;(e)t=0.05 sFig.16.Comparison of three-dimensional water-entry cavities of calculative and experimental results:(a)t=0.01 s;(b)t=0.02 s;(c)t=0.03 s;(d)t=0.04 s;(e)t=0.05 s.

圖17 并聯入水空泡試驗與數值計算對比(v0=1.9 m/s) (a)試驗結果;(b)數值計算結果Fig.17.The water-entry cavity in paraller of experimental results and numerical results.

圖18 并聯入水位移特性數值計算結果與試驗結果對比Fig.18.Comparison of the numerical results and experimental results.

由于試驗過程中難以捕捉空泡橫截面形狀,因此我們采用數值模擬結果對三維空泡演化模型的正確性進行驗證[22].為驗證數值計算結果的有效性,圖17給出了回轉體以1.9 m/s速度并聯入水過程中,入水空泡形態實驗與數值計算結果的對比.圖18分別給出了回轉體并聯入水過程空泡形態時歷演化與角位移、線位移時歷曲線的對比.從圖中可以看出,數值計算所得的空泡形態在兩彈軸線內側區域的發展程度較試驗結果略大,但空泡形態輪廓的整體演化與試驗符合度較好.位移特性曲線與試驗結果符合較好.綜上分析,可認為本文數值方法適用于回轉體并聯入水過程的研究.

圖19給出了t=0.05 s時,四個不同深度處空泡界面理論值與數值仿真結果的對比.從圖中可以看出,計算結果與數值結果具有較高的符合度,表明引入影響函數后的三維空泡演化計算模型的正確性,基于該模型可較為準確地預測空泡在三維空間的演化過程.

圖19 空泡截面形狀理論結果與數值結果對比(t=0.05 s)Fig.19.Comparison of the cavity cross-section of calculative and experimental results.

6 并聯入水空泡三維形態演化特性研究

不同于單獨入水過程的軸對稱空泡,并聯入水空泡半徑沿回轉體軸線呈非均一分布,且在空泡的不同發展階段,空泡隨周向的變化亦呈現出不同的變化規律.圖20給出了極坐標系下t=0.05 s時,不同深度處空泡半徑隨極角(范圍取0—π)的變化規律,此時空泡已在回轉體表面形成閉合,圖20(a)給出了閉合點上方空泡半徑隨極角的變化,圖20(b)給出了閉合點下方空泡半徑隨極角的變化.從圖中可以看出,在閉合點上方,隨著入水深度的增加,空泡半徑隨極角的變化呈現出從正相關到負相關的變化;在閉合點下方,隨著深度的增加,空泡半徑呈現出從負相關到正相關的變化.該現象的產生主要是受空泡頸縮的影響,在閉合點上方,隨著入水深度增加,空泡截面逐漸靠近閉合點,此時,自由演化區空泡(θ=π/2—π)隨著入水深度增加,收縮量增大;抑制演化區,有勢壁面對空泡的收縮亦存在抑制作用,空泡收縮速率低于自由演化區,使得在閉合點附近,抑制演化區的空泡半徑大于自由演化區,進而形成了隨著入水深度的增加,空泡半徑隨極角的變化呈現出從正相關到負相關變化的現象.在閉合點下方,靠近閉合點處,即H=6.1D處,空泡截面處在收縮過程中,其半徑隨極角的變化呈負相關的原因同上;隨著深度的增大,空泡截面的運動從收縮過渡至擴張,在該過程中,抑制演化區受有勢壁面影響,擴張受限,使得自由演化區空泡半徑大于抑制演化區,因而空泡半徑隨極角變化呈現出正相關特性.

從圖20中還可以發現,在閉合點上方,無論是自由演化區還是抑制演化區,空泡半徑隨入水深度的增大呈單調減小趨勢;在閉合點下方,抑制演化區空泡半徑隨入水深度的增大單調減小,而自由演化區空泡半徑隨深度增加呈先增大后減小的趨勢.該現象與空泡截面的發展程度有關,在閉合點上方,各空泡截面均已充分發展并進入收縮階段,因此空泡半徑隨入水深度具有較好的單調性;而在閉合點下方,自由演化區尚有未完全發展的空泡截面,因而出現了空泡半徑先增大后減小的趨勢.

為分析有勢壁面對并聯入水空泡半徑影響的空間變化規律,定義并聯入水空泡加權半徑如下:

其中,r為并聯入水空泡半徑,rc2為未受有勢壁面影響的單獨入水空泡半徑.

圖21給出了空泡加權半徑隨極角的變化規律,同樣,圖21(a)曲線給出了閉合點上方不同深度處的半徑變化,圖21(b)曲線給出了閉合點下方不同深度處的半徑變化.從圖21(a)中可以看出,在閉合點上方,隨著入水深度的增加,抑制演化區空泡半徑與自由演化區空泡半徑的比值逐漸增大,出現該現象的主要原因在于抑制演化區的空泡收縮率遠小于自由演化區.而對于閉合點下方,圖21(b)中可以看出隨著入水深度的增大,抑制演化區空泡半徑與自由演化區空泡半徑的比值隨深度增加先減小后增大,且當深度較大時,其值非常接近.

圖20 空泡半徑沿周向變化規律(t=0.05 s) (a)閉合點上方;(b)閉合點下方Fig.20.The cavity radius of circumferential direction.

圖21 抑制演化區空泡加權半徑沿周向變化規律(t=0.05 s) (a)閉合點上方;(b)閉合點下方Fig.21.The of the suppressed region.

圖22給出了t=0.05 s時不同深度處空泡截面形態,其中圖22(a)為閉合點上方不同深度空泡截面形態,圖22(b)為閉合點下方不同深度空泡截面形態.在閉合點上方,空泡經歷了較為充分的演化,使得空泡有了明顯的擴張、收縮運動,隨著深度增大,空泡截面逐漸縮小.在H=1.1D處,空泡截面形成了過度演化,即空泡截面邊界在x方向超越了空泡的理論x最大值——空泡對稱線處的空泡形態x值.分析其形成原因,在該深度處,收縮勢較弱,空泡擴張程度較大,然而隨著極角的增大,有勢壁面對擴張的抑制逐漸減弱,在該位置處,空泡的擴張程度與抑制程度的比值超過了對稱線處空泡擴張程度與抑制程度的比值,使得空泡形成過度演化.空泡的過度演化只形成于深度較淺的位置,在深度較深的位置,空泡擴張程度總體較弱的地方難以形成過度演化,如圖22(b)所示.

圖22 不同深度處空泡截面形態(t=0.05 s) (a)閉合點上方;(b)閉合點下方Fig.22.The cross section shape of various depth.

圖23分別給出了H=1.3D,H=3.3D,H=5.3D三個深度處極坐標系下不同時刻的空泡形態.從圖中可以看出,隨著時間的增加,極坐標系下的空泡半徑呈先增大后減小的趨勢,且增大速率隨著極角的增大而增大.該過程反映了空泡界面的經典演化特性.在空泡發生收縮時,由于影響函數在極角越大處產生的收縮抑制越小,使得極角較大的位置率先發生收縮,而此時極角為0處的空泡尚未形成收縮.隨著深度增大,極角較大位置的空泡收縮速率越快.

圖23 極坐標系下空泡截面半徑時歷演化 (a)H=1.3D;(b)H=3.3D;(c)H=5.3DFig.23.Time evolution of cavity cross section shape in polar coordinate system:(a)H=1.3D;(b)H=3.3D;(c)H=5.3D.

圖24給出了極坐標系下不同時刻的空泡加權半徑隨極角的變化規律.從圖中可以看出,空泡加權半徑與空泡截面半徑隨時間的變化規律基本一致.此外,從圖中還可以看出,在空泡從擴張向收縮過渡的過程中,空泡加權半徑逐漸靠近,在H=3.3D處,t=0.03 s與t=0.04 s的加權半徑已接近完全重合.

圖25給出了笛卡爾坐標系下的空泡形態時歷演化,從圖25(a)中可以發現,在空泡形成之初,空泡尚未出現過度演化現象,隨著時間的推移,空泡過度演化逐漸產生,其程度也逐漸增大,在空泡的收縮過程中,過度演化逐漸得到緩和.而隨著深度的增大,在空泡演化的整個過程中,均沒有過度演化現象產生.

圖24 極坐標系下空泡加權半徑時歷演化 (a)H=1.3D;(b)H=3.3D;(c)H=5.3DFig.24.Time evolution of in polar coordinate system:(a)H=1.3D;(b)H=3.3D;(c)H=5.3D.

圖25 笛卡爾坐標系下空泡截面形態時歷演化 (a)H=1.3D;(b)H=3.3D;(c)H=5.3D.Fig.25.Time evolution of in Cartesian coordinate system:(a)H=1.3D;(b)H=3.3D;(c)H=5.3D.

7 結 論

本文基于勢流理論,通過二維軸對稱方法分析了回轉體單獨入水過程空泡動力學模型.基于回轉體單獨入水空泡的動力學模型,引入有勢壁面和影響函數,建立有勢壁面影響下的空泡受迫演化模型,并基于該模型分析了并聯入水空泡三維演化特性,得到如下結論.

1)回轉體入水過程流場速度勢可以看作由一個隨回轉體運動的點源和位于空泡軸線處的線源疊加產生,其中空泡的擴張運動主要受點源的影響,而收縮運動主要受線源影響.

2)在并聯入水過程中,雙空泡演化在空間呈鏡面對稱,空泡間的相互擾動可以通過引入有勢壁面進行分析.有勢壁面對空泡的演化呈抑制作用,該抑制作用包含兩個方面,分別為對擴張的抑制和對收縮的抑制.

3)并聯入水空泡半徑隨極角的變化與空泡截面所處深度有關,在靠近閉合點附近的抑制演化區空泡截面半徑隨極角的增大而逐漸減小,遠離閉合點處的抑制演化區空泡截面半徑隨極角的增大而增大,空泡與半徑規律相反.

4)在深度較淺處,空泡擴張過程中會形成過度演化,空泡收縮階段過度演化逐漸被削弱并消失.