高功率微波輸出窗內側擊穿動力學的PIC/MCC模擬研究?

左春彥 高飛 戴忠玲 王友年

(大連理工大學物理學院,三束材料改性教育部重點實驗室,大連 116024)

(2018年6月27日收到;2018年9月28日收到修改稿)

1 引 言

隨著高功率微波(highpowermicrowave,HPM)器件輸出功率提高及脈寬增加,介質輸出窗的放電擊穿已成為HPM產生與傳輸的重要限制因素[1?3].放電擊穿是一系列復雜物理過程共同作用的結果,它是由二次電子觸發,并與介質窗表面釋放出的氣體發生非彈性碰撞,最終導致放電擊穿.國內外學者對于介質二次電子倍增現象已經開展了許多相關的理論和實驗研究.在國際上,Neuber等[4,5]進行了HPM窗口擊穿實驗,利用光學診斷給出了介質沿面閃絡與放電擊穿的物理圖像;Kishek等[6,7]發展了蒙特卡羅方法預估二次電子倍增的敏感區間;Kim和Verboncoeur[8,9]利用一維PIC/MC(particle in cell/Monte Carlo)程序,研究了介質二次電子倍增和表面氣體碰撞電離過程;Nam和Verboncoeur[10]利用模擬結果修正電子能量分布函數來完善整體模型.

在國內,常超等[11?15]研究了介質窗周期性矩形和三角形表面輪廓對倍增的抑制機制、解吸附氣體和磁場對窗口倍增的影響以及微波脈沖尾部對窗口破裂的增強;郝西偉等[16]分析了二次電子的運動軌跡,給出了電子運動狀態隨電子發射參數和微波場參數的變化規律,并分析了介質窗表面及內部的導電樹枝通道的發展過程;蔡利兵等[17?20]通過一維PIC/MC模擬研究了外加磁場或強直流場時次級電子倍增和氣體電離等過程,同時給出了表面釋氣速率對氣體擊穿的影響規律;Cheng和Liu[21]利用傳輸線模型,研究了微波磁場和斜入射微波對電子倍增的影響;董燁等[22?28]利用PIC/MC模擬給出了二次電子倍增的物理過程及特性物理量的變化,研究了釋氣強度及釋氣分子的運動速率對介質沿面閃絡擊穿的影響,并利用PIC/MC與三維電磁流體耦合模型模擬了電磁場對介質窗表面閃絡擊穿過程的影響.

然而,迄今人們對介質窗倍增放電達到飽和并向氣體電離轉換過程的研究尚不完善,尤其是低氣壓條件下,關于微波頻率和微波振幅對介質窗擊穿時氣體電離出現的時間和位置的影響還需要進一步深入地研究.因此,本文采用自主研發的1D3V PIC/MC程序,詳細研究了真空及不同氣壓條件下介質表面擊穿過程中的二次電子倍增形成機制以及電子與背景氣體碰撞電離的轉換過程,并給出了電子密度、離子密度、電場的空間分布,重點考察了低氣壓條件下微波頻率和微波振幅對氣體電離出現的時間和位置的影響.

2 物理模型

圖1為介質沿面閃絡擊穿的示意圖,其中假定:微波沿?x方向傳輸,入射電場平行于介質表面沿y方向,Ew=Erf0sin(ωt+ θ),其中Erf0為微波場的幅值矢量,ω=2πf為微波的角頻率,f為微波頻率,θ是0時刻微波的初始相位.在局部電場增強誘發場致發射或X射線、紫外線在介質表面引發光電發射,初始種子電子由介質表面出射,并在介質表面束縛電荷場(由電子發射后正電荷積累形成)作用下,從微波電場Ew中獲得能量后加速撞擊介質表面,激發二次電子,如此往復從而出現二次電子倍增效應.電子從微波場中加速獲得能量后,與介質表面附近的氣體分子發生碰撞電離,形成新生電子和正離子并形成等離子體.

圖1 高功率微波介質沿面閃絡擊穿的示意圖Fig.1.Schematic of the multipactor on dielectric surface under HPM.

2.1 PIC/MC模型

本文采用PIC/MC模擬的一維空間分布、三維速度分布(1D3V)模型,對介質表面擊穿過程進行模擬.初始化時,將一維空間劃分為許多均勻的網格,將帶電粒子隨機地分布在這些空間格點上,同時粒子速度為三維且服從麥克斯韋分布.帶電粒子的運動規律由方程(1)和(2)確定:

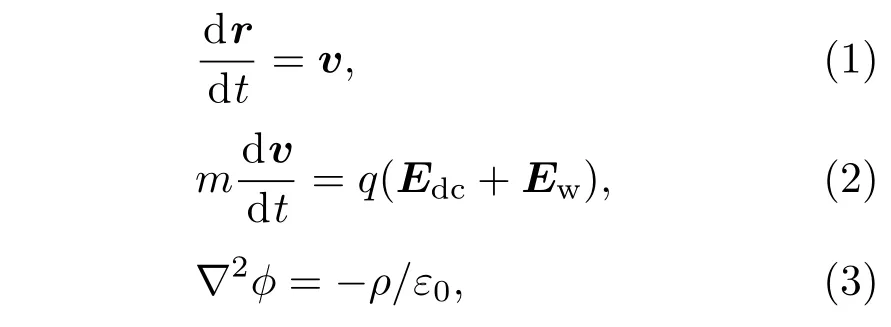
其中m和q是帶電粒子的質量和電荷;dr是dt時間內粒子的位移,v是該時刻粒子的速度,?是空間電勢,ρ是電荷密度,ε0是真空介電常數.在給定初始條件下,采用顯示蛙跳格式數值求解運動方程(1)和(2),可以得到不同時刻x方向上粒子的運動信息,并由此統計出不同時刻帶電粒子的電荷密度分布∑.然后,對泊松方程(3)進行數值離散,并采用追趕法進行求解,可以得到不同時刻電勢?的空間分布,進而通過中心差分得到靜電場Edc.當電子與氣體分子碰撞時,則采用MC方法來確定帶電子與中性粒子的碰撞細節,包括電子彈性碰撞后的散射方向和非彈性碰撞的能量損失等.在模型中具體考慮的碰撞類型有電子與中性原子的彈性、激發和電離碰撞,離子與中性粒子的彈性碰撞和電荷交換碰撞等.當粒子運動到介質窗邊界時,應用次級電子發射模型來判斷二次電子產額;當粒子運動至右側自由空間邊界時,利用吸收粒子邊界條件來模擬粒子逃逸情況.

2.2 次級電子發射模型

本文采用Vaughan提出的經驗公式來描述次級電子產生率與初級電子的能量ε及入射角度α之間的關系[29]:

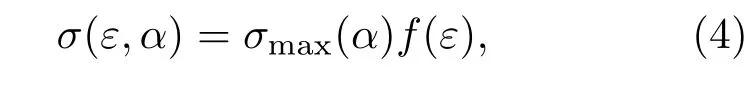
式中

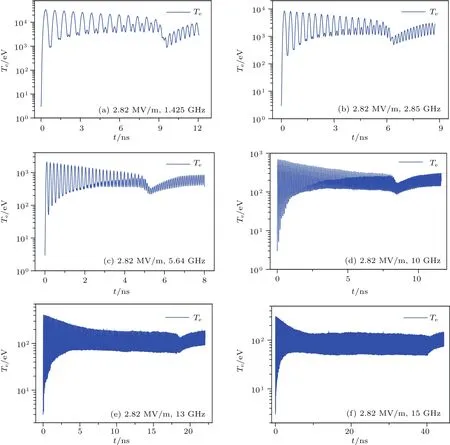
其中σ為次級電子發射率;σmax為正入射次級電子最大發射率,Emax為其對應的入射能量;σmax(α)為斜入射次級電子最大發射率,Emax(α)為其對應的入射能量;α為入射角(α=0代表正入射,α=π/2代表掠入射);ks為表面光滑系數(ks=0,1,2分別代表粗糙、不光滑和光滑);Ei為電子的碰撞能量,Eth為閾值.當Ei1區間(E1

次級電子初始能量概率密度函數滿足[6]:

次級電子發射角發射角φ是偏離平行介質表面方向的角度,概率密度函數g(φ)=0.5sinφ,0<φ<π;E0m是次級電子能量分布函數峰值處對應的能量,通常取2—10 eV,本文取為2 eV.

3 數值模擬結果與分析

采用上述模型和模擬方法,可以對真空及不同氣壓下介質表面放電擊穿過程中二次電子倍增的形成機制、電子與背景氣體碰撞電離的多物理轉換過程開展系統的研究.選取參數如下:模擬區域為介質窗內側3 mm,微波電場幅值0.2—5 MV/m,微波頻率1.425—15 GHz,氣壓0—760 Torr,初始種子電子密度2.45×1014m?3.本文選取介質材料為聚四氟乙烯,其次級電子倍增材料特性參數為:Emax0=400 eV,σmax0=2.12,ks=1. 由于沒有考慮材料表面氣體退吸附過程,我們假定模擬區域有無限的背景氣體.模擬中選用Ar為背景氣體,其碰撞截面數據從國際原子能機構網站數據庫獲得[30].因為介質表面電子運動的平均自由程遠小于微波的波長,所以不考慮微波場在傳播方向上的分布,模擬中設定微波場僅隨時間變化.

圖2顯示的是介質材料聚四氟乙烯的二次電子發射產額δ隨入射電子能量ε及入射角度α的變化關系.隨著電子入射能量的增加,二次電子產額先增加后下降[3,31],隨著電子入射角度的增加(0—90?)二次電子產額增加,尤其是在高能區域該現象更為明顯.另外,產額曲線與δ=1的直線有兩個交叉點εp1(約55 eV)和εp2(約4600 eV),表示入射電子能量在兩個交叉點之間時,介質的二次電子發射產額大于1.

3.1 氣壓對擊穿放電的影響

圖3和圖4中的計算結果在數值計算時,選取微波頻率為2.85 GHz,微波幅值Erf0為2.82 MV/m.圖3給出了真空、10 mTorr,500 mTorr,10 Torr,760 Torr五種條件下電子(e)和氬離子(Ar+)的數量、電子的平均能量Te隨微波作用時間的演化規律.在真空條件下,由于僅存在介質窗上二次電子的倍增效應,故不存在氣體電離產生的Ar+,如圖3(a)所示.在放電初期,電子轟擊介質窗,然后介質窗發射二次電子,同時二次電子發射量大于入射電子量.由此導致介質窗上積累正電荷,其產生沿介質窗法線方向的靜電電場Edc,并加速電子轟擊介質窗,產生出更多的二次電子.介質窗累積的正電荷將產生更強的直流電場,如此重復,直至介質窗處電子平均能量不斷降低到二次發射閾值為1的臨界能量,這時達到倍增飽和,同時微波周期平均的電子數量和電子能量不再變化,如圖3(a)和圖3(b)所示.電子倍增飽和后,電子數量和平均能量均以2倍于微波的頻率振蕩.

圖3 在(a),(b)真空,(c),(d)10 mTorr,(e),(f)500 mTorr,(g),(h)10 Torr,(i),(j)760 Torr條件下電子及Ar+數量、電子平均能量的時間演化規律Fig.3.Temporal evolutions of the number of electrons and Ar+,and of the corresponding statistic electron energy at(a),(b)the vacuum,(c),(d)10 mTorr,(e),(f)500 mTorr,(g,h)10 Torr,and(i),(j)760 Torr.

在極低壓(10 mTorr)時,粒子數目的時間演化呈現兩個階段,如圖3(c)所示,即二次電子倍增階段(6 6.10 ns),電子數目隨時間呈現指數增長;當二次電子達到飽和(>6.10 ns),出現氣體碰撞電離的過程,此后電子數目以2倍微波頻率振蕩的同時以指數增長速度增加,而離子數目僅以指數增長速度增加.值得注意的是,10 mTorr條件下在6.10 ns發生氣體擊穿,相比于其他氣壓的擊穿時刻(如500 mTorr時6.22 ns,10 Torr時6.82 ns)稍早,是因為氣壓較低,粒子的碰撞自由程較大,電子在微波場中加速時間更長,獲得能量較大,且放電初期快速產生二次電子后,介質窗遺留的正電荷約束電子的運動時間,使其平均能量逼近二次電子倍增區間,如圖3(d),并快速達到倍增飽和,發生氣體擊穿.然而擊穿發生后粒子密度的增長較緩慢且平均電子能量有緩慢抬升,這說明此時二次電子倍增效應和氣體碰撞電離過程是耦合在一起的,且兩者相互促進,但由于此時氣壓較低電離強度比較弱,粒子增長較慢.電子平均能量的逐漸升高是因為出現氣體電離后,Ar+數目增多,由于離子質量遠大于電子質量,所以Ar+幾乎不響應微波場的振蕩,因此電子移位后,遺留的正離子會增加靜電電場的振蕩幅值,從而導致電子平均能量在氣體電離之后逐漸增加.

在低氣壓(500 mTorr)時,與10 mTorr類似,粒子數目的時間演化呈現兩個階段,如圖3(e)所示,即二次電子倍增階段(6 6.22 ns)和二次電子倍增與體電離共存階段(>6.22 ns).與10 mTorr不同的是,氣壓的升高使得氣體電離強度增大,粒子密度在氣體擊穿后快速升高,電子平均能量的升高速度也增加.

在高氣壓(10 Torr)時,如圖3(g)和圖3(h)所示,與低氣壓類似,也包含二次電子倍增階段(6 6.82 ns)和二次電子倍增與體電離共存階段(>6.82 ns).不同的是,氣壓大幅升高使得氣體電離強度大幅度增加,氣體擊穿后的瞬間氣體大量電離,粒子密度迅速升高,電子平均能量則急劇減小.

在極高壓(760 Torr)條件下,電子及Ar+隨著時間的增加呈現指數增長,并且電子數目略低于Ar+的數目,如圖3(i)所示.此時,等離子體放電擊穿過程由氣體碰撞電離主導放電,無明顯的二次電子倍增.圖3(j)給出的是電子平均能量隨時間的演化規律.在放電初期,電子平均能量迅速增加到6.5 eV左右,然后以微波頻率的2倍頻率做小幅振蕩.這是因為高氣壓下,電子自由程較短,電子與中性氣體頻繁碰撞,從而導致電子平均能量較低.

圖4給出了真空,10 mTorr,500 mTorr,10 Torr和760 Torr五種條件下的介質表面擊穿放電穩態后微波周期平均的電子密度、Ar+密度及靜電場的空間分布.結果顯示:在真空條件下,電子密度隨著距離的增加先緩慢下降,后迅速下降,最后幾乎不變,密度的分布幾乎在介質表面的10μm厚度內;而靜電場隨著距離的增加單調下降,大約在300μm厚度時衰減到0.這是因為沒有氣體的存在,介質表面的擊穿放電只存在二次電子的倍增過程,二次電子發射后介質表面形成的靜電場是正值,電子被靜電場牢牢地約束在介質表面.

在10 mTorr條件下,如圖4(c)和圖4(d)所示,電子密度有一個很小的峰值并在8—92μm內保持平穩,離子密度在8μm內迅速增加,后與電子一樣保持平穩分布,但在92μm后兩者同時迅速衰減至0附近.可以看出8μm內二次電子倍增主導放電,8—92μm氣體電離發揮主要作用.靜電場在8μm內由0.5 MV/m迅速降低至0 MV/m,最后在0 MV/m附近波動.

在500 mTorr條件下,如圖4(e)和圖4(f)所示,電子密度隨距離的增加先下降到一個極小值(約8μm處),后增加到一個極大值(約16μm處),最后單調下降.Ar+密度隨距離的增加先增加后下降,峰值中心約在16μm處.這是因為在介質表面10μm以內區域,二次電子倍增主導放電;在遠離介質表面的區域,氣體碰撞電離主導放電.靜電場隨距離的增加先從0.7 MV/m下降到?0.4 MV/m,再增加到0.3 MV/m左右,然后下降到0 MV/m,最后在其附近波動.靜電場是由介質表面二次電子發射后積累的正電荷和氣體電離產生的電子與Ar+的空間分布差異所決定的.

在10 Torr條件下,電子密度與Ar+密度空間分布基本一致,隨著距離的增加先增加后下降,密度的峰值中心約在40μm處.這表明此時擊穿放電主要由氣體電離主導,而二次電子倍增過程被抑制.而靜電場的分布為介質表面處為負向(指向介質表面方向),隨著遠離介質窗,靜電場絕對值逐漸減小,后幾乎在0附近波動.

在760 Torr條件下,電子密度與Ar+密度空間分布一致,在介質窗表面附近很低,在遠離介質窗后逐漸升高,124μm之后波動變化.靜電場在10μm以內幾乎不變(?0.19 MV/m),然后絕對值逐漸減小到0 MV/m,最后在0附近波動.這是因為在如此高的氣壓下,二次電子發射完全被抑制,介質表面的擊穿放電主要由氣體電離主導.此外,在760 Torr條件下,電子密度和Ar+密度與10 Torr條件下的密度相比較低,這是因為在高氣壓下電子的自由程非常小,平均電子能量較低(6—7 eV),電離率較低,因此粒子密度較低.

比較圖4(a)—(i),電子密度的峰值中心逐漸遠離介質表面,例如在真空,10 mTorr,500 mTorr,10 Torr,760 Torr條件下,電子密度的峰值中心分別約在0,8,16,40,124μm.這是二次電子倍增和氣體電離相互競爭的結果,二次電子倍增是在介質表面產生,而氣體電離在等離子體體區內產生,可以看出,隨著氣壓的升高,氣體電離的優勢逐漸增大.

圖4 在(a),(b)真空,(c),(d)10 mTorr,(e),(f)500 mTorr,(g,h)10 Torr和(i),(j)760 Torr條件下微波周期平均的電子、Ar+及靜電場Edc的空間分布Fig.4.The time-averaged spatial distributions of electron density,Ar+density and Edcat(a),(b)vacuum,(c),(d)10 mTorr,(e),(f)500 mTorr,(g,h)10 Torr and(i),(j)760 Torr.

3.2 500 mTorr下微波幅值及微波頻率對擊穿放電的影響

圖5給出了500 mTorr,f=2.85 GHz條件下,不同微波電場幅值下氣體電離放電擊穿發生的時間及電子密度峰值中心的位置.結果顯示:在2.85 GHz微波下,隨著微波電場幅值的增加,氣體電離放電擊穿發生的時間先下降后增加;而放電擊穿后電子密度的峰值中心與介質表面的距離隨著微波電場幅值的增加而單調下降,即微波電場幅值越大,氣體電離放電擊穿發生的位置越靠近介質窗表面.尤其當微波頻率(GHz)是微波電場幅值(MV/m)的2倍左右時,氣體電離放電擊穿發生的時間較早.原因如圖6(d)所示,當微波頻率為微波電場幅值的2倍左右時,平均電子能量在二次電子倍增階段變化范圍是80—2150 eV,剛好處于圖2所示的二次電子產額大于1的區間,且對應的二次電子產額數值較大,因此二次電子倍增飽和的過程最快.然而微波電場的幅值過低或過高,均會導致平均電子能量過低或過高,從而使得二次電子的產額減小,最終導致二次電子倍增飽和過程減緩,使得氣體電離放電擊穿的時間較晚.

圖5 500 mTorr,2.85 GHz時氣體電離放電擊穿發生的時間點t0及放電擊穿后峰值中心位置d0隨微波幅值的變化Fig.5.The change of the time point of gas breakdown and the distance of the electron density peak away from the dielectric window with the microwave amplitude,at 500 mTorr,f=2.85 GHz.

圖6 在500 mTorr,2.85 GHz及不同微波振幅幅值(a)0.2 MV/m,(b)0.5 MV/m,(c)1 MV/m,(d)1.425 MV/m,(e)2.82 MV/m,(f)5 MV/m下平均電子能量的時間演化規律Fig.6.Variations of the statistic electron energy with time t at different microwave amplitudes E0(a)0.2 MV/m,(b)0.5 MV/m,(c)1 MV/m,(d)1.425 MV/m,(e)2.82 MV/m and(f)5 MV/m,with microwave frequency and background gas pressure fixed at 2.85 GHz and 500 mTorr,respectively.

圖7給出了500 mTorr,Erf0=2.82 MV/m條件下不同微波頻率下氣體電離放電擊穿發生的時間及電子密度峰值中心的位置.結果顯示:隨著微波頻率的增加,氣體電離放電擊穿發生的時間先下降后增加;而放電擊穿后電子密度的峰值中心與介質表面的距離隨著微波頻率的增加是先升高后下降.同樣值得注意的是,當微波頻率(GHz)是微波電場幅值(MV/m)的2倍左右時,氣體電離放電擊穿發生的時間較早.產生這一現象的原因和圖6所示的原因一致,如圖8(c)所示,當微波頻率是微波電場幅值的2倍左右時,在二次電子倍增階段的平均電子能量正好處在二次電子產額最大的區間.

圖7 500 mTorr,2.82 MV/m時氣體電離放電擊穿發生的時間點t0及放電擊穿后峰值中心位置d0隨微波頻率的變化Fig.7.The change of the time point of gas breakdown and the distance of the electron density peak away from the dielectric window with the microwave frequencies,at 500 mTorr,Erf0=2.82 MV/m.

圖8 在500 mTorr,2.82 MV/m及不同的微波頻率(a)1.425 GHz,(b)2.85 GHz,(c)5.70 GHz,(d)10.00 GHz,(e)13.00 GHz,(f)15.00 GHz下平均電子能量的時間演化規律Fig.8.Variations of the statistic electron energy with time t at different microwave frequencies(a)1.425 GHz,(b)2.85 GHz,(c)5.70 GHz,(d)10.00 GHz,(e)13.00 GHz and(f)15.00 GHz,with the background gas pressure and microwave amplitude fixed at 500 mTorr and 2.82 MV/m,respectively.

4 結 論

本文針對HPM介質窗內側氬氣放電擊穿過程建立了一維(1D3V)模型,并開發了PIC/MC程序,模擬研究了氣壓、微波電場幅值及微波頻率對HPM介質窗放電擊穿中等離子體的產生和演化過程.結果顯示:在真空條件下,介質窗放電擊穿只存在二次電子倍增過程;在低氣壓(10 mTorr,500 mTorr)和稍高氣壓(10 Torr)條件下,介質窗放電擊穿過程由二次電子倍增主導放電轉化為二次電子倍增和氣體電離共存放電;在極高氣壓條件下(760 Torr),介質窗放電擊穿由氣體電離主導.同時給出了不同氣壓下電子、離子的密度和靜電場的空間分布,結果顯示,氣壓的增加使得電子密度的峰值中心逐漸遠離介質窗.此外,在500 mTorr條件下當微波振幅增加時,氣體電離放電擊穿發生的時間先提前后延遲.這一現象通過次級電子發射模型進行了解釋,即當微波電場幅值增大時,二次電子倍增過程中電子的平均能量增加,導致二次電子發射產額變大,倍增過程更易達到飽和,從而使得氣體電離提前產生;然而當微波電場幅值過大時,電子的平均能量過高,導致二次電子產額反而降低,從而使得氣體電離推遲產生.而且氣體電離產生的電子密度峰值中心隨著微波振幅的增加而逐漸靠近介質窗方向,即在高微波振幅條件下氣體電離在更靠近介質窗的位置發生.同時,當固定微波振幅增加微波頻率時,氣體電離放電擊穿的時間也是先提前后延遲;并且體電離產生的電子密度峰值中心隨著微波頻率的增加,先遠離介質窗后靠近.尤其當微波頻率(GHz)是微波振幅(MV/m)的2倍左右時,氣體電離出現的較早.綜上所述,在實際HPM應用過程中可以調節微波的振幅、頻率及氣壓等,來實現推遲氣體電離的出現,從而增加微波的傳輸效率.

感謝西北核技術研究所高功率微波重點實驗室基金的支持和常超研究員對本論文的幫助.