發電廠架空導線載流量計算方法的研究

王 麗，李紀華

(國核電力規劃設計研究院有限公司，北京 100095)

發電廠架空導線載流量計算，在國內電力工程電氣設計手冊第一冊(簡稱手冊)[1]中用簡化公式進行核算；而在 IEC TR 61597—1995(簡稱IEC)[2]及 IEEE Std 738—2006[3](簡稱IEEE)標準中，是根據熱平衡方程，代入不同的環境條件參數后進行核算；3個標準中的方法并不完全相同。

本文以某涉外發電廠工程設計為例，通過手冊、IEC和IEEE標準，對架空導線載流量的3種不同計算方法進行定量計算和分析比較，確定了不同方法的適用范圍，為涉外工程設計提供一定參考。

1 架空導線載流量的3種計算方法

1.1 手冊中導體載流量的簡化計算法

手冊中導體載流量簡化計算公式為[1]

(1)

結合某涉外工程的環境條件和導線選型等因素，各參數取值見表1。

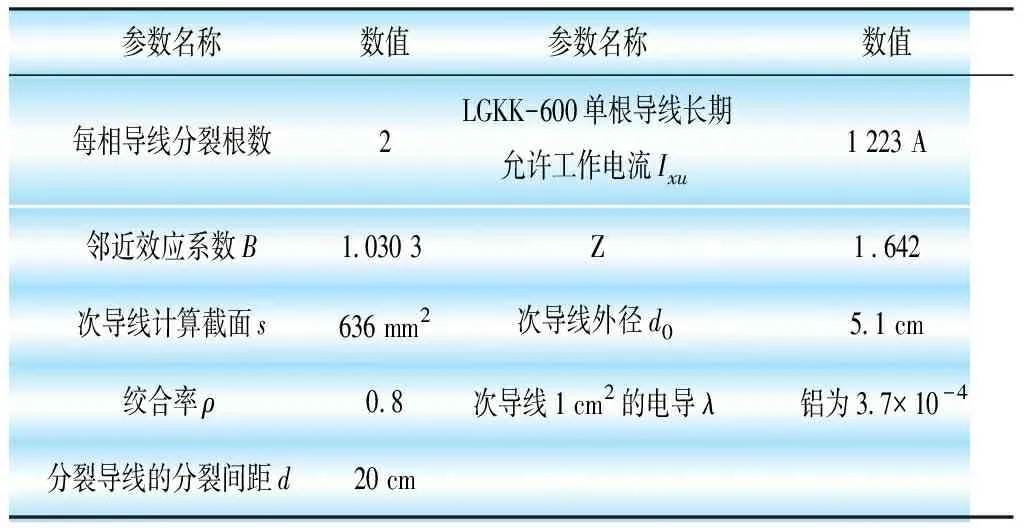
表1 手冊中各參數取值

這種簡化算法，是在特定的氣象條件(導線最高允許工作溫度80 ℃、環境溫度25 ℃、導體表面黑度為0.9等條件)下算出的實際載流量，受導線排列方式、分裂根數、分裂間距等因素的影響，裕度大，沒充分發揮導線的載流能力。

1.2 IEC標準中架空導線載流量計算方法

IEC法根據導體的發熱條件，以導線的熱平衡方程為依據，計算導體的穩態工作電流[2]，即：

Pj+Psol=Prad+Pconv

(2)

=2×1 348.33=2 696.67(A)

(3)

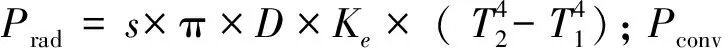
結合某涉外工程，各參數取值見表2。

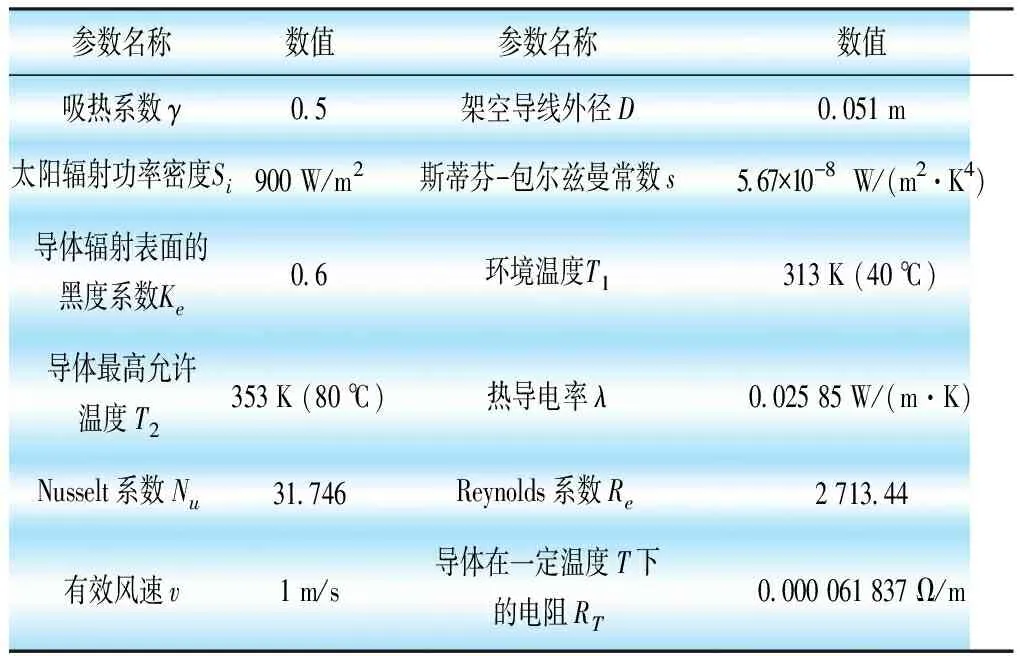
表2 IEC法中各參數取值

該計算方法考慮了環境溫度和風速等參數對載流量的影響，較手冊法計算結果更貼近實際環境情況，適合手工計算。該計算結果能夠保證導線強度和運行安全，但假設條件裕度仍很大，沒有考慮不同時刻、季節環境變化等因素，結果保守，沒有充分發揮線路載流能力。

1.3 IEEE標準中架空導線載流量計算方法

IEEE法也是基于熱平衡原理提出的，其基本公式為

(4)

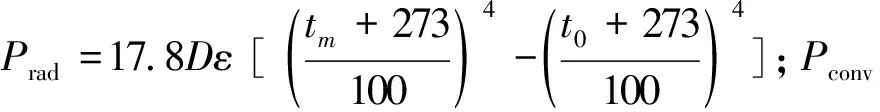
結合某涉外工程，各參數取值見表3和表4。

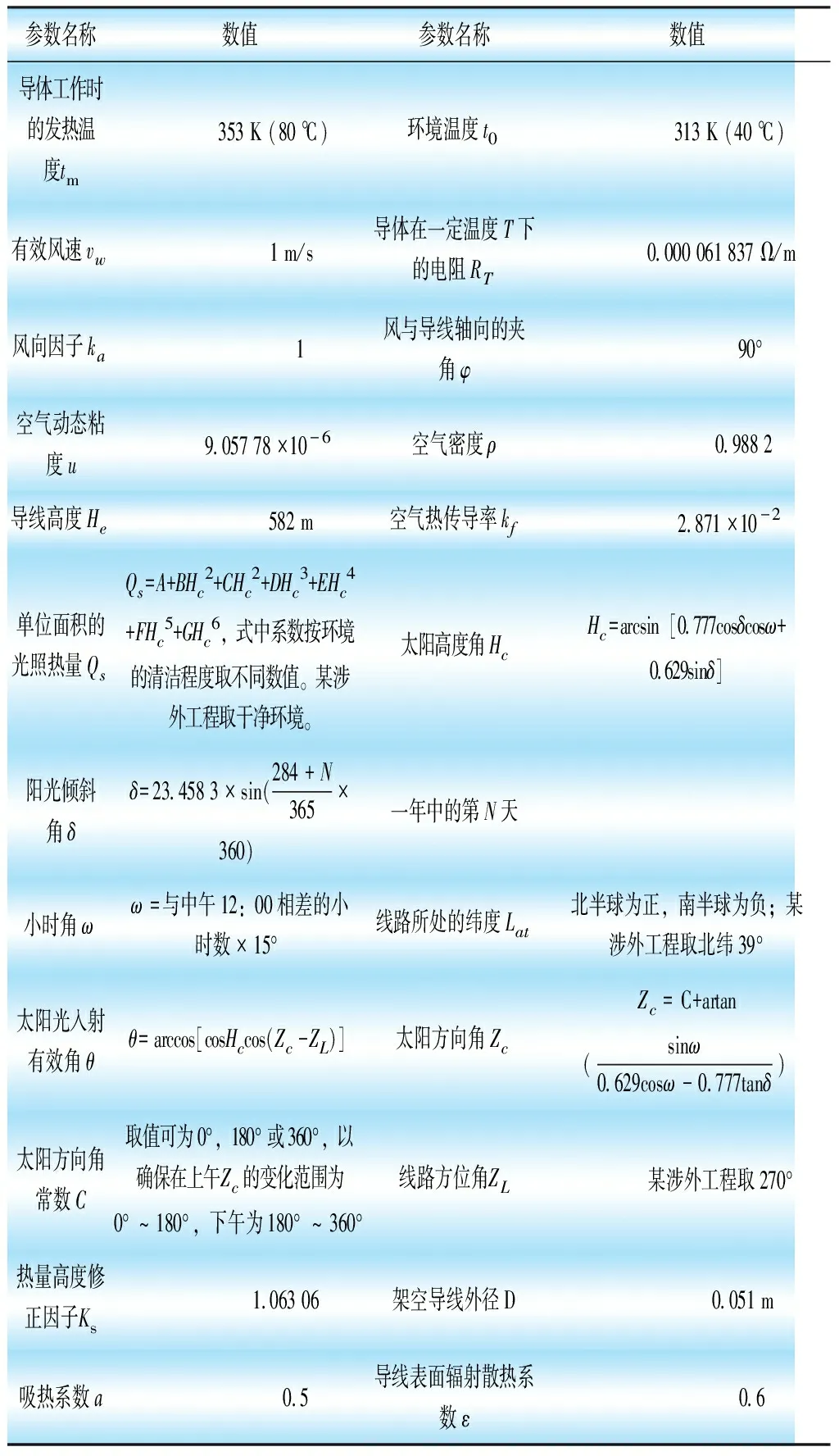
表3 IEEE法中各參數取值

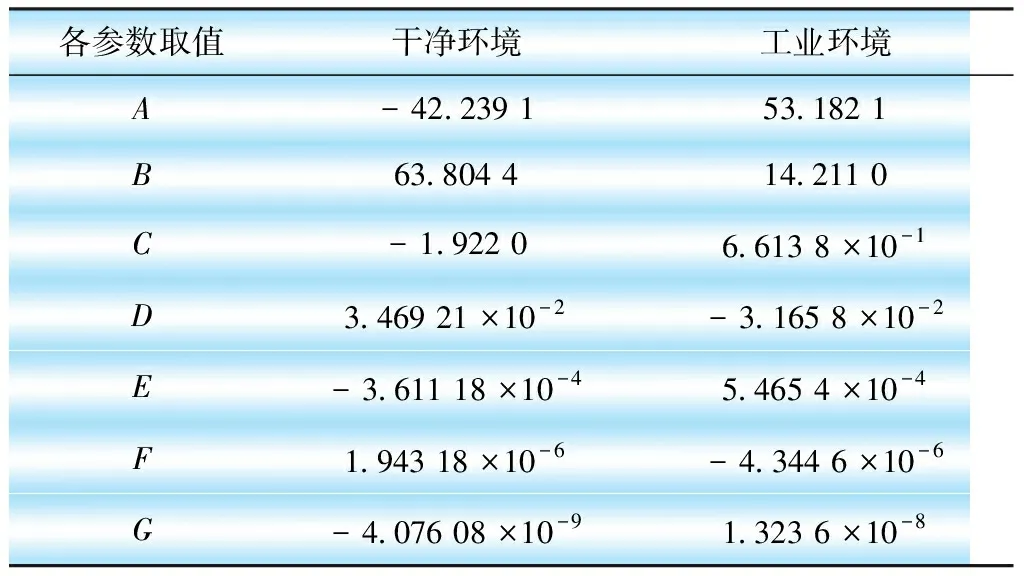
表4 單位面積的光照熱量QS中系數取值表

從表4中參數取值可以看出IEEE法，除考慮環境溫度、風速的影響，還考慮導線所處緯度、季節、時間、環境、導線高度和走向等，所得結果隨時間變化，更貼近實際情況。

2 3種計算方法的定量比較和分析

結合某涉外工程選用的架空導線2為例，按照手冊法、IEC法和IEEE法進行計算。80 ℃為導線允許溫度，導線海拔高度582 m，環境溫度取40 ℃，風速1 m/s，80 ℃時導體的交流電阻為0.000 061 837 Ω/m。3種方法計算出的輻射散熱率、對流散熱量、日照吸收熱量對比，見表5。IEC法和IEEE法計算出的輻射散熱率差異不大；對于對流散熱量， IEC法隨環境溫度、風速變化，而IEEE法算出的數值隨海拔高度、環境溫度、風速等變化；對于日照吸收熱量，IEC法與時間無關，IEEE法隨時間變化。

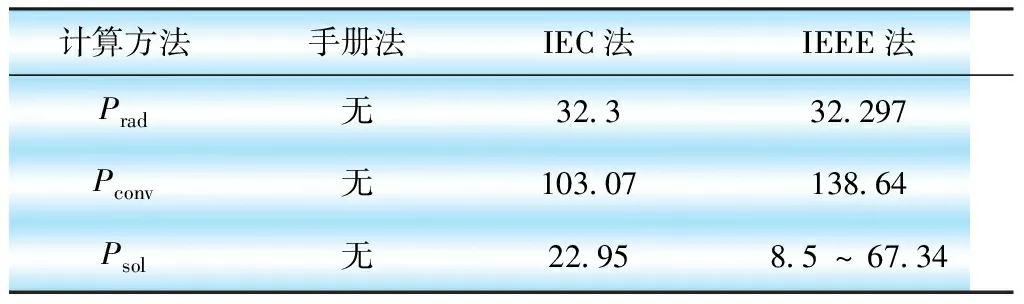
表5 手冊法、IEC法和IEEE法計算結果比較 W/m

對表5中差別比較大的對流散熱量、日照吸收熱量分別進行定量分析和比較。并對3種方法最后算出的導線實際載流量進行對比。

2.1 對流散熱量與海拔高度的關系

IEC法與海拔高度無關，IEEE法與海拔高度有關，主要體現在空氣密度上，海拔高度越高，空氣密度越小，對流散熱量也越小。結合某涉外工程參數，分別用IEC法和IEEE法算出的對流散熱量結果如圖1所示。由圖1可見，隨溫度升高，對流散熱量下降。隨海拔高度升高，IEC法對流散熱量不變，而IEEE法對流散熱量下降。隨環境溫度下降，IEEE法由上到下的曲線分別為導線處在海拔高度0 m、500 m、1 000 m、1 500 m、2 000 m時的對流散熱量計算值。由圖1可知，在導線高度低于1 000 m時，海拔高度引起的對流散熱量誤差小于5.98%，而導線高度高于1 000 m時，海拔高度引起的對流散熱量誤差介于5.98%～11.96%。所以低海拔時，對流散熱量的誤差小。

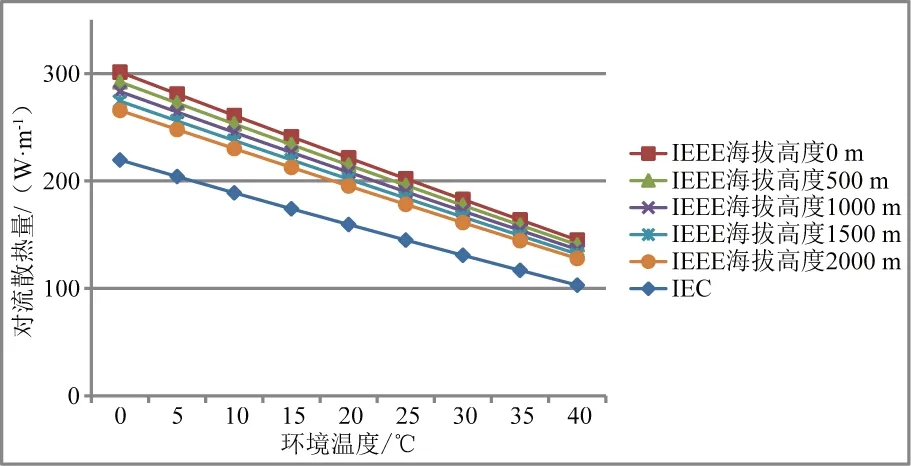
圖1 IEEE法/IEC法中對流散熱量Pconv隨環境溫度及海拔高度的變化情況

2.2 對流散熱量與風速的關系

IEC法、IEEE法都與風速有關，風速越大，對流散熱量也越大，但兩者受風速的影響不同。結合某涉外工程參數，分別用IEC法和IEEE法對對流散熱量結果進行對比，如圖2所示。由圖2可知，隨著風速增加，對流散熱量上升。IEEE法算出的對流散熱量略高于IEC法。從圖1可知，當風速較低時，兩者的對流散熱量差別不大。對于無法獲得實時風速的情況，要考慮到導線的熱穩定，往往對風速的估計值都偏小，以保證求出的載流量不致引起導線溫度越限，所以低風速下兩種方法算出的對流散熱量差異小。

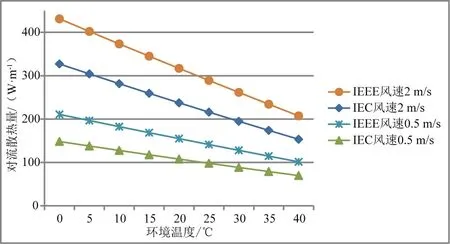
圖2 IEEE法/IEC法中對流散熱量Pconv隨風速的變化

2.3 日照吸收熱量與時間的關系

日照吸收熱量的計算結果，IEEE法與IEC法差別極大。結合某涉外工程參數，分別對IEC法和IEEE法計算出的日照吸收熱量結果進行對比，如圖3所示。2017年4月7日(N=97)導線2的日照吸收熱量，導線為北緯39°，海拔高度為582 m，導線表面吸熱系數取0.5，導線方向角為270°，算出的6：00—18：00日照吸收熱量。

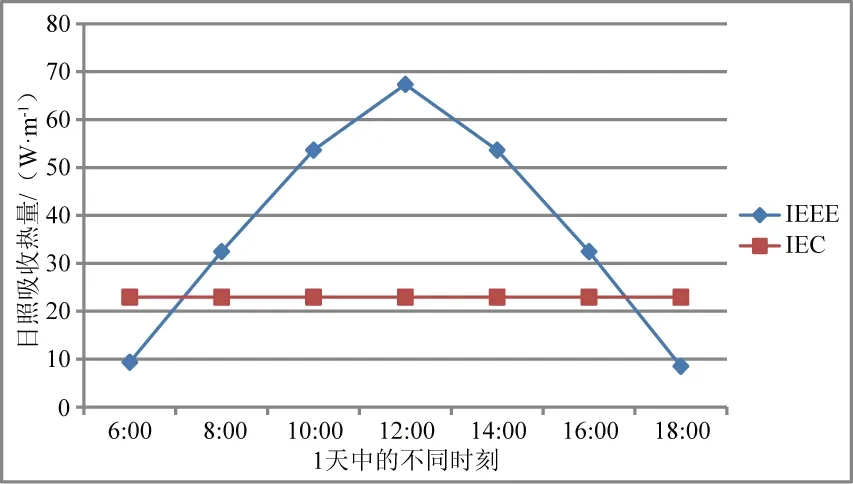
圖3 IEEE法/IEC法中日照吸收熱量Psol與時刻的關系

從圖3可知，IEC法的計算結果為1條水平線，即日照吸收熱量不隨時間變化，為22.95 W/m。而IEEE法的計算結果為1條曲線，在12：00達到峰值，為67.34 W/m，顯然這更符合導線的實際情況。由此可知，IEC法計算出的日照吸收熱量在部分時候偏大，導致計算出的導線載流量偏小，所以按IEC法計算出的載流量偏保守。此外，在6：00前和18：00后，IEEE法計算出的日照吸收熱量迅速下降，這時候沒有陽光，求出的日照吸收熱量無意義。同理，在采用IEC法計算載流量時，夜晚也不應該計及日照吸收熱量。

2.4 3種方法計算出的載流量結果對比

3種方法計算出的載流量結果對比，如圖4所示。其中手冊法計算出的載流量最低，為2 000.1 A，裕度過大；IEC法計算的載流量為2 696.67 A，考慮了環境因素，基本能保證導線長期運行載流量，裕度大；而IEEE法計算的載流量與時間有關，最大值為3 241.517 A，最小值為2 588.676 A，波動較大，并隨時間變化。從IEEE法計算結果可以看出，架空導線的實際載流量存在極大的隱性容量，根據IEEE法精確計算結果，可以指導線路的動態增容，可增容10%～30%。

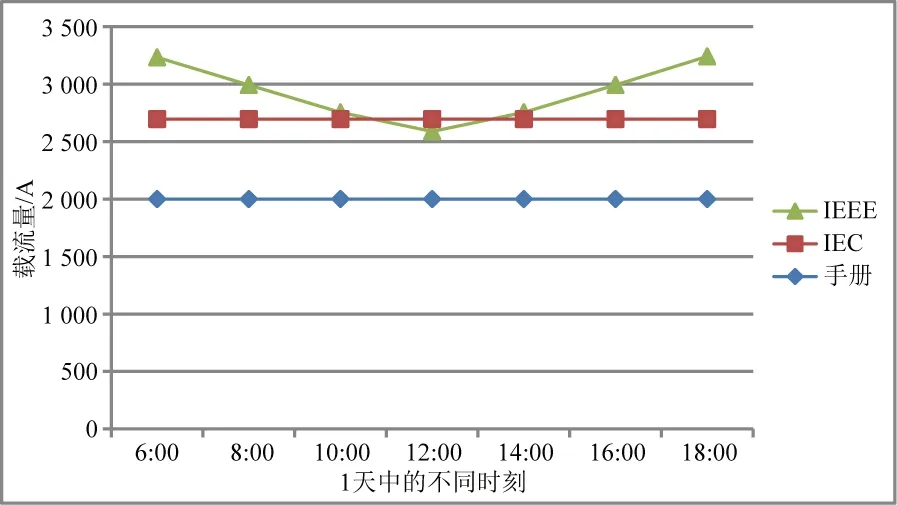
圖4 3種方法計算的載流量結果比較

由計算結果可見，用手冊法計算導線載流量能確保導線的熱穩定，但裕度太大，沒有充分發揮導線的載流能力；用IEC中方法計算載流量，計算所需要的變量少，計算過程簡單，適合于計算導線的長期運行載流量；用IEEE中方法計算載流量需要的變量多，計算過程較復雜，但在一些特殊情況下，能夠用于計算導線一段時間過負荷能力。

2.5 方案比較

手冊法考慮的環境因素最少，與IEC法和IEEE法計算原理不同。國外IEC法和IEEE法架空導線載流量計算方法是基于熱平衡公式提出的，考慮環境因素不同，所以計算復雜程度不同，現主要比較IEC法、IEEE法2種計算方法之間的區別。

a.經IEC法、IEEE法計算輻射散熱量的變量和系數完全相同。

b.用IEC法公式計算對流散熱量，其變量是氣溫和風速；而IEEE法涉及到的變量除了氣溫和風速外，還有風向、導線海拔高度等。低風速時，對流散熱量公式采用Pconv1，高風速時采用Pconv2。IEEE法中的導線海拔高度對對流散熱量的影響主要體現在空氣密度上，海拔高度越高，空氣密度越小，對流散熱量的值也越小。風速越大，對流散熱量也越大。對于無法獲得實時風向、風速的情況，考慮到導線的熱穩定，對風速的估計值都偏小，以保證求出的載流量不致引起導線溫度越限，所以在低風速下，IEC法、IEEE法計算出的對流散熱量差異小。在導線海拔高度小于1 000 m、風速低的情況下，對流散熱量差異也不大。

c.經IEC法、IEEE法計算出的日照吸收熱量差別巨大。IEC法采用簡單公式即可算出結果，而IEEE法考慮了所處的緯度、季節、時間、環境、導線高度和走向等因素，所得的結果隨時間變化。IEC法計算出的日照吸收熱量，部分情況偏大，導致計算出的導線載流量偏小，所以按IEC法計算出的載流量偏保守。

2.6 先進技術應用和技術經濟分析

a.靜態設計載流量：手冊法和IEC法算出的載流量是在特定的氣象條件和導體最高允許工作溫度下算出的載流量，屬于靜態設計載流量，該結果基本能夠保證導線強度和運行安全，但由于假設條件裕度過大，未考慮不同時刻、季節環境變化，所以結果偏保守。

b.動態載流量：IEEE法的載流量算法，雖然也是假設在周圍氣象條件恒定不變的情況下導出的，但根據國外經驗，該方法也適用于采用實時氣象數據的動態載流量計算，計算方法涉及到更多的變量，計算過程相對復雜，計算出的線路動態載流量更為準確。

c.設計技術經濟對比分析：根據2013年版《電力建設工程裝置性材料預算價格》[5]，某涉外工程選取的2鋁鋼擴徑空心導線的預算價格約為20 928元/t，總用量約為1.44 km，折合重量3.873 6 t ，按此計算，架空導線的工程造價約8.106 67萬元。雖然在發電廠各類電氣設備中，架空導線價格不占主要部分，但如果能合理計算導線載流量，選取更經濟可靠的導線型號，可充分發揮導線的載流能力，尤其對長距離輸電線路，結合實時氣象指導動態增容后，將更為節省工程整體造價。

3 結論

建議今后涉外工程架空導線載流量計算時，不同計算方法的適用范圍如下。

工程條件在海拔1 000 m以下、風速低于0.5 m/s時，3種方法計算結果接近，均可計算架空導線實際載流量。

工程條件在海拔1 000 m以上或風速高于0.5 m/s時，三者差異較大。具體結論如下：

a.不建議采用手冊法，裕度過大，不能充分發揮導線載流能力；

b.IEC法計算長期運行允許載流量，基本保證導線強度和運行安全；

c.IEEE法計算一段時間內導線載流量或短時過負荷情況。尤其對長距離線路，可指導線路動態增容，發揮導線實際載流能力。