基于閉塞時間理論的移動閉塞追蹤間隔時間特性研究

劉文慧，苗建瑞

(1. 北京交通大學軌道交通控制與安全國家重點實驗室，北京 100044；2. 北京交通大學交通運輸學院，北京 100044)

隨著社會經濟的發展，客貨運輸需求持續增長，提升軌道交通的運輸能力成為亟待解決的現實問題，提高信號系統的效能是一種低成本、高效益的方式[1]。隨著現代控制技術的進步，保證前后行列車之間安全間隔的閉塞方式由固定閉塞方式向移動閉塞方式轉變，在保證行車安全的前提下，大為縮短了追蹤間隔時間，行車效率也得到了極大地提高。

在高速鐵路列車追蹤間隔研究方面，張岳松[2-3]等在CTCS(Chinese Train Control System)-2/3的連續曲線控車模式下，借鑒普速鐵路列車間隔時間的計算方法，給出高速鐵路列車間隔時間的定義及其計算方法，分析了影響高速列車追蹤間隔時間的主要因素。劉曉娟等[4]針對CBTC(Communication Based Train Control System)的特點，在城市軌道交通列車移動閉塞的背景下，提出了列車追蹤間隔時間的表達式，分析了影響移動閉塞列車運行追蹤間隔的本質因素，提出了追蹤時間間隔的優化方法。劉暢等[5]在常規的列車追蹤運行模型的基礎上，提出了一種考慮前車位置與速度的新追蹤模型，該模型大大減小了列車的追蹤間隔。Tazoniero等[6]為了充分發揮移動自動閉塞的優勢，實現列車追蹤間隔距離的最小化，提出了一種同步控制策略，能保證前后行追蹤列車之間的運行間隔達到最小。上述關于列車間隔時間的研究,主要基于列車牽引的仿真方法實現追蹤間隔時間的計算,雖然研究工作取得了顯著的進展，但對間隔時間計算方法的研究大多是靜態的，并且缺少對影響追蹤間隔要素的定量研究分析。

本文基于閉塞時間理論(Blocking Time),設計移動閉塞追蹤間隔時間計算方法，開發相應的間隔計算工具，并對影響追蹤間隔的要素進行定量分析，研究各因素對列車追蹤間隔的影響規律。

1 閉塞時間理論

閉塞時間理論認為，某列車在某段時間內獨占某個閉塞分區，包括列車到達前信號準備、接近，列車在閉塞分區中運行，以及列車離開閉塞分區的出清和信號轉換時間[7]。在列車行進過程中，可以形成該列車對該區間的閉塞時間帶,如圖1所示。

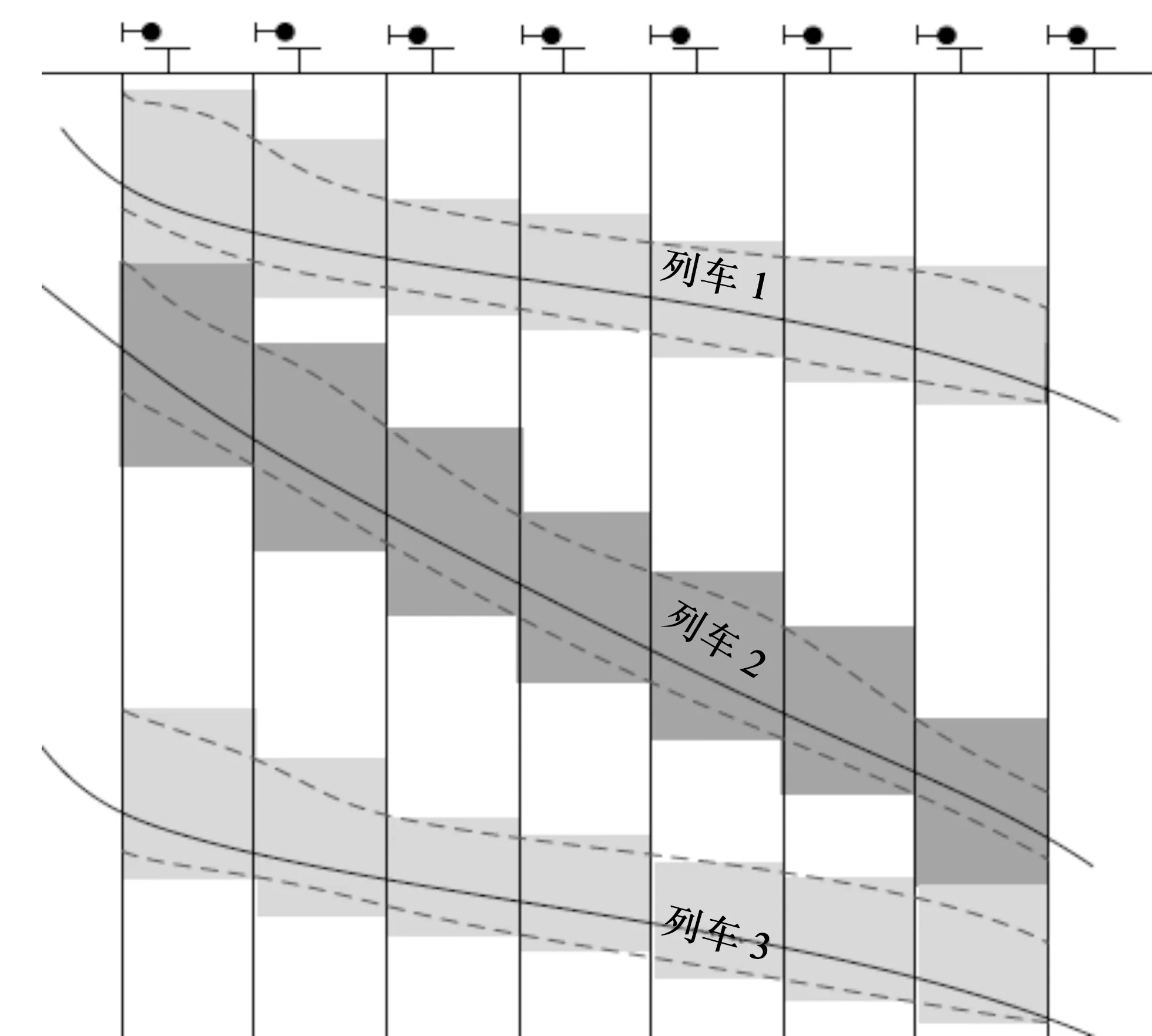
圖1 閉塞時間帶Fig.1 Blocking time belt

固定閉塞的閉塞時間帶圖示中是離散的時間區塊，移動閉塞的圖示則會變成一條連續的帶狀。通過該方法，分別計算出每列車在區間中每一個空間位置的占用范圍，生成該列車的時間占用帶，只要保證前后行列車的“占用帶”不重疊，即可計算得到前后列車的追蹤間隔時間。

2 列車對區間的時間占用計算

基于閉塞時間理論，對列車通過區間某點前后，對其產生的占用時間組成進行分析，進而得出列車對區間某點的占用時間帶，如圖2所示。

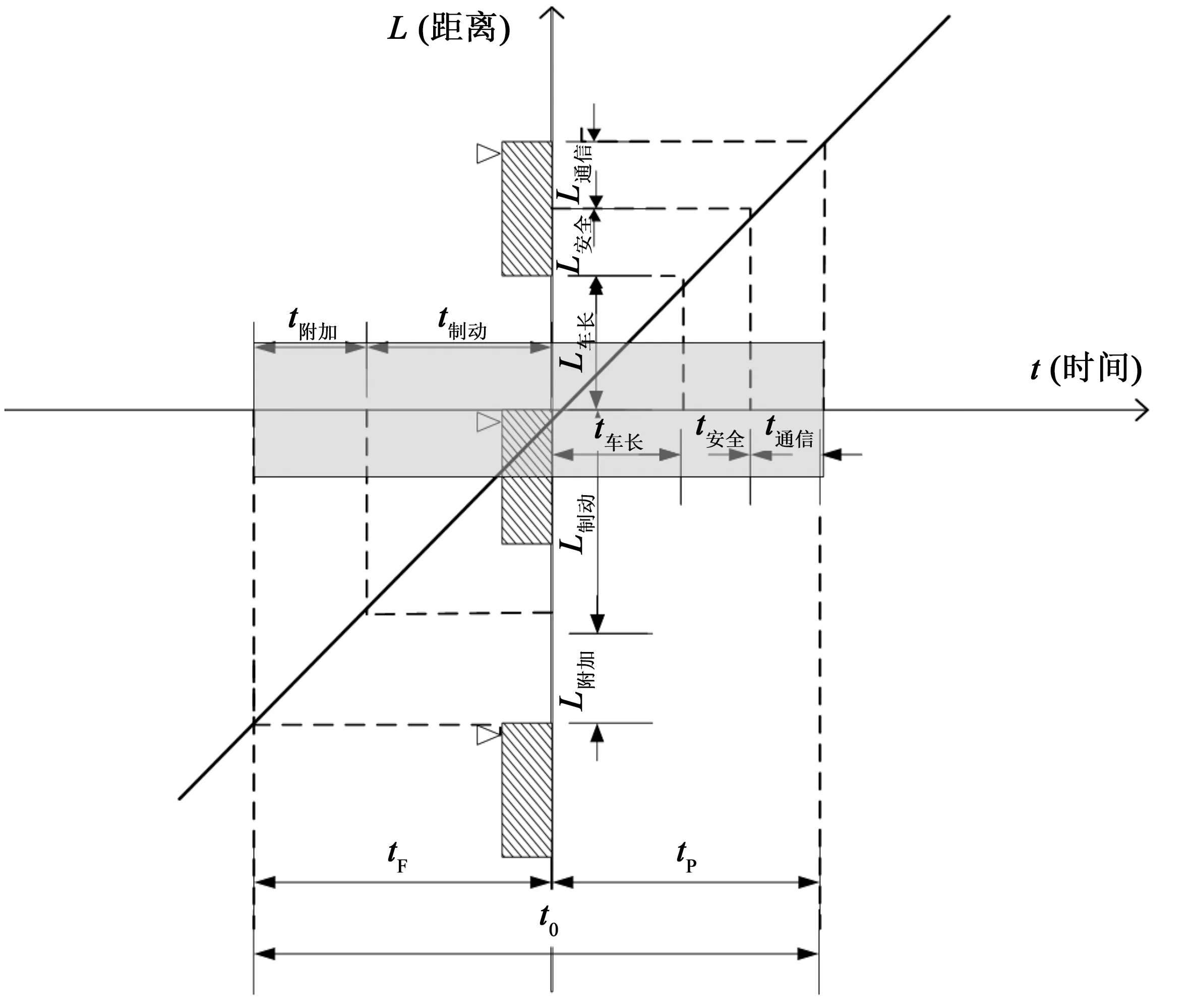
圖2 閉塞時間計算示意圖Fig.2 Schematic diagram of Blocking Time calculation

2.1 預占用計算

由于列車從運行速度制動至靜止需要經過一段時間，期間走行一定的距離，因此列車在通過區間的某點前的一段距離內，已經提前對該點進行獨占。該段占用的時間在圖2中可表示為：

tF=t附加+t制動，

(1)

式中,tF為列車對區間某點的預占用時間；t附加為發出制動指令后，從原狀態轉換至制動力實際產生狀態過程內列車的空走時間；t制動為列車以運行速度走過一個制動距離所花費的時間。

2.2 出清占用計算

列車車頭通過區間該點后，還需要走行一個列車長度的距離車尾才能夠出清該點，在車尾出清該點后，還需要走行一個安全距離，該點的占用狀態才能夠被釋放。列車向后車或調度中心發出釋放占用信號后要花費一定的時間才能被后車確認[8]。因此列車在車頭通過某點后，還需要延續一段時間，才能釋放對該點的占用，該段占用的時間在圖2中可表示為：

(2)

式中，tp為列車對區間某點的清空時間；t列車為列車的運行速度走行一個列車長度的距離L列車所花費的時間；t安全為列車的運行速度走行一個安全距離L安全所花費的時間；t通信為列車向后行列車或調度中心發出釋放占用信號且被后車確認的通信時間。

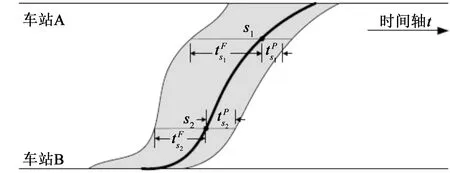
圖3 列車占用時空分布圖Fig.3 Space-time distribution map of train occupancy

2.3 占用時間帶計算

列車對區間內某點的預占用時間與出清占用時間共同構成了列車對該點的占用時間帶，占用時間帶總占用的時間在圖2中可表示為

tO=tF+tP，

(3)

式中，tO為列車對區間某點的占用時間帶時間。

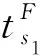
3 基于重疊法的追蹤間隔計算方法

3.1 追蹤間隔的數學描述

如圖4中所示，設車站A的中心線里程為SA，車站B的中心線里程為SB，計算區間為從車站A的中心線到車站B的中心線，對于前后行列車的間隔時間，只需要保證列車在計算區間上任意一點的占用時間帶均不重合即可，則前后行列車的出發追蹤間隔：

(4)

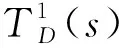
圖4 前后行列車發車間隔時間計算示意圖Fig.4 Diagram of headway calculation for train departure

對于每個計算點，分別計算按照該計算點的前后行間隔時間可以確定的列車出發時間間隔，然后對于所有的計算點，取最大的追蹤間隔時間作為列車從前方站出發的間隔時間。

3.2 追蹤間隔計算方法設計

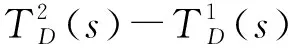
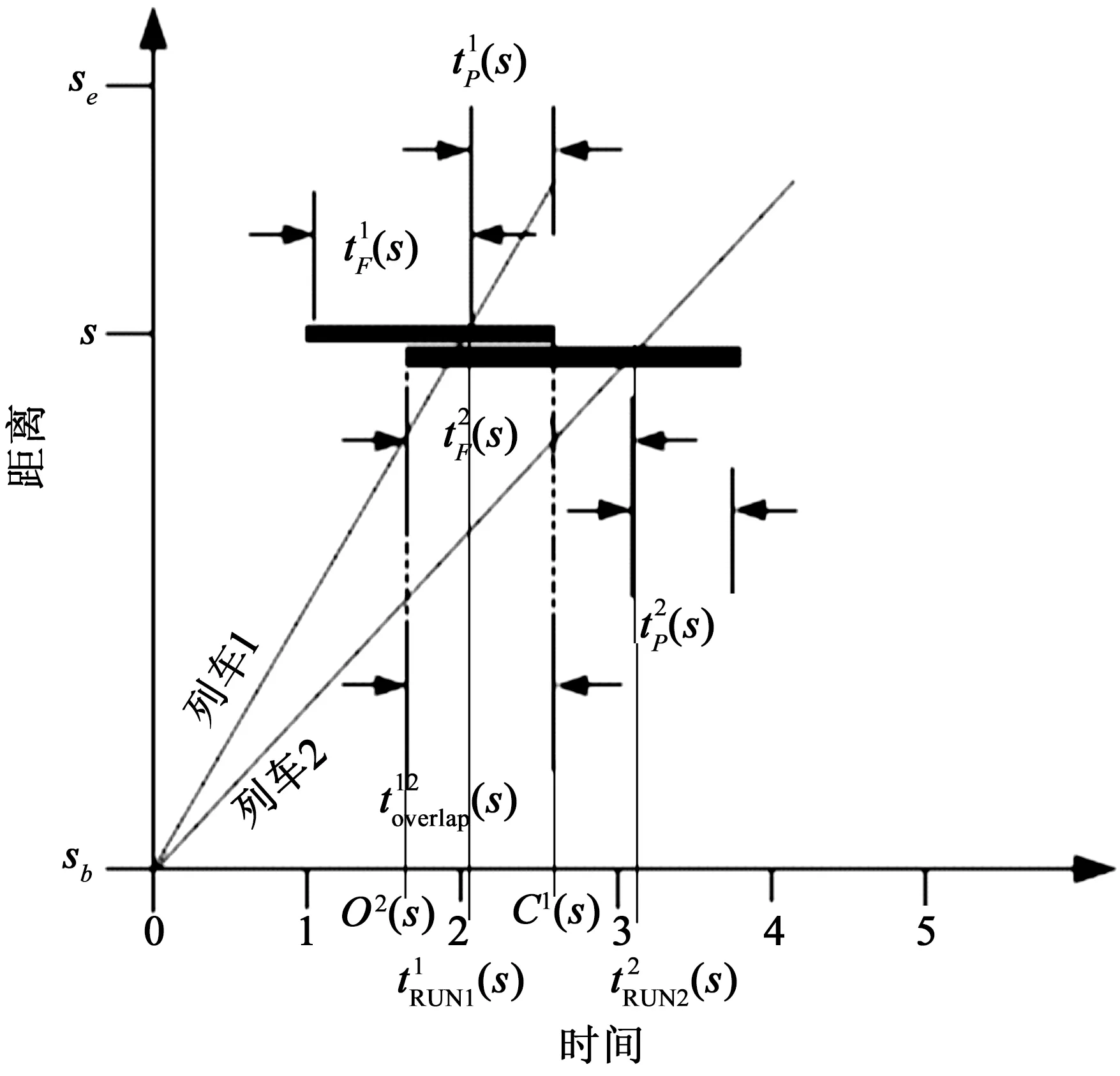
圖5 重疊法計算追蹤間隔原理Fig.5 Principle of overlapping method for calculating the tracking headway

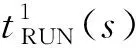
(5)

列車2開始占用s點的時刻：

(6)

兩列車占用s點的時間段發生重疊的時間量為：

(7)

當兩列車速度相等時，公式(7)可化簡為

(8)

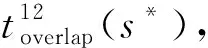
4 列車追蹤間隔時間影響要素分析

在visual studio平臺上搭建仿真環境，利用本文給出的追蹤間隔計算方法，定量分析列車長度、列車運行速度、列車牽引制動性能及進路鎖閉和解鎖方式等因素[9-10]對追蹤間隔時間的影響規律。

4.1 列車長度影響分析

對不同限速下的長編組及短編組300型動車組，仿真計算其區間追蹤間隔時間、車站發車-發車間隔時間、車站到達-到達間隔時間，分析結果如表1所示。

表1 不同限速下長編組與短編組間隔時間對比

由表可分析得出，當列車長度增大時，3種間隔時間均相應增大，且與短編組的追蹤間隔保持相同的趨勢，只是在短編組基礎上增加了一個較為固定的時間量。不同的是，區間追蹤間隔時間的時間增加量比較小，車站發車-發車時間間隔與車站到達-到達時間間隔比區間追蹤間隔時間的時間增加量要大得多，且車站發車-發車時間間隔與車站到達-到達時間間隔的時間增加量相近。這主要是由于限制間隔時間的瓶頸點在于發車進路與到達進路的末端軌道區段，在列車處于低速狀態時，長度的延長會較大地延遲該軌道區段的解鎖時刻，從而造成追蹤間隔變大。但由于列車在進出站時的速度相差不大，進路長度也相差不大，因此長編組列車的到達和出發時間間隔與短編組的增大量比較接近。

4.2 列車運行速度影響分析

對不同限速下的動車組，計算其區間追蹤間隔時間，其變化趨勢如圖6所示。

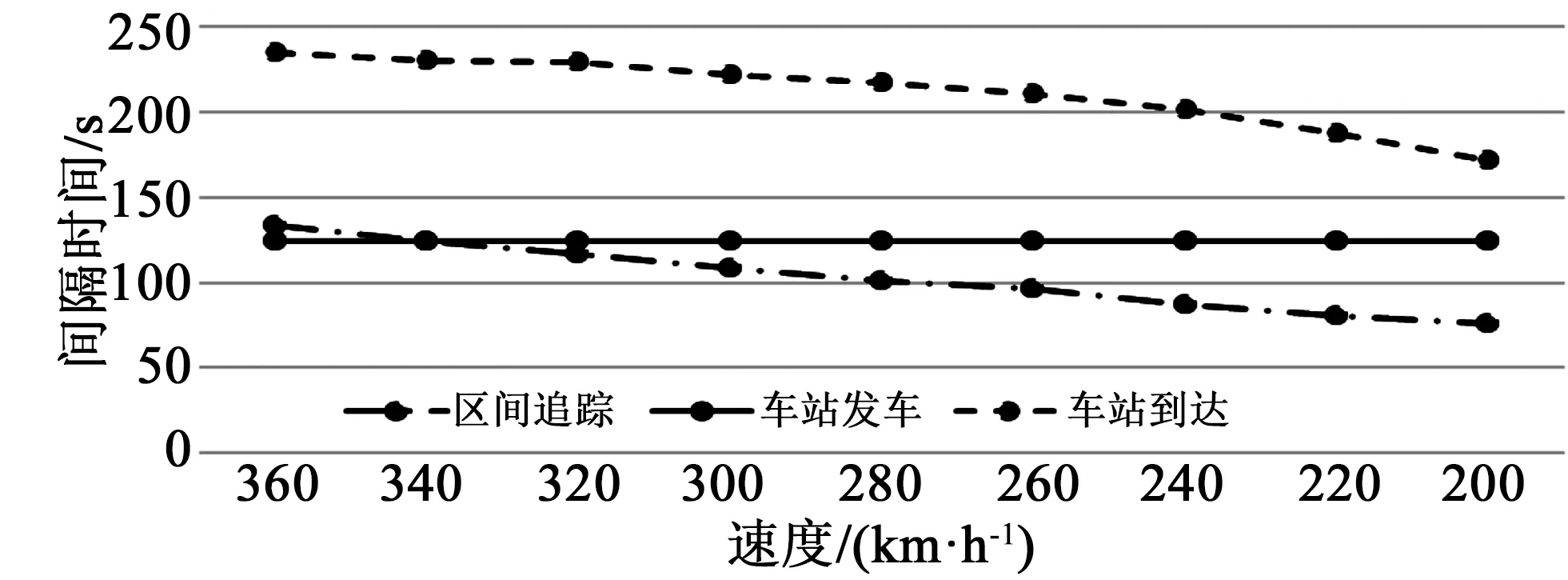
圖6 動車組間隔時間隨速度變化趨勢圖Fig.6 The headway trend diagram of EMU with speed

由圖6中可看出，區間追蹤間隔時間隨著速度降低基本呈線性關系下降。車站發車-發車間隔時間并不隨限速的改變而改變，這主要是由于列車在發車時處于啟動加速狀態，還未達到限速，因此限速的改變并不會對發車-發車間隔產生影響。總體而言，車站到達-到達間隔時間隨著速度的降低而減小。

4.3 列車牽引制動系統性能分析

在忽略輪軌黏著限制的前提下，對列車的牽引加速度及制動加速度按照1.05的倍率增大，分別進行10次實驗，根據結果數據分別計算區間追蹤間隔、車站出發-出發間隔、車站通過-通過間隔以及車站到達-到達間隔時間。

由圖7可看出，增大列車加速性能僅會影響列車車站出發間隔時間，當加速度以1.05的倍率增大時，車站出發間隔時間將以約0.99的倍率減小；由圖8可看出，增大列車制動性能會在很大程度上降低列車除車站出發間隔時間外的所有間隔時間，當制動加速度以1.05的倍率增大時，車站到達、車站通過和區間追蹤間隔呈現相同的下降趨勢和斜率，這些間隔時間將以約0.97的倍率減小。

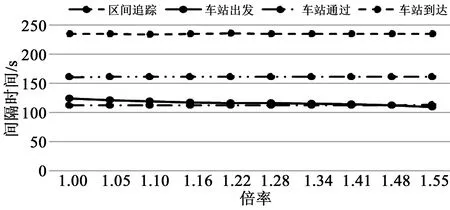
圖7 動車組間隔時間隨牽引加速度變化趨勢Fig.7 The headway trend diagram of EMU with traction acceleration

圖8 動車組間隔時間隨制動加速度變化趨勢Fig.8 The headway trend diagram of EMU with braking acceleration

4.4 進路鎖閉和解鎖方式影響分析

目前我國鐵路聯鎖中對進路的鎖閉和解鎖方式基本都實行一次鎖閉，分段解鎖的方式。為了測試進路分段鎖閉的效果，我們針對動車組設計了分段鎖閉的實驗，計算列車到達-通過間隔時間，得到結果如表2所示。

表2 進路分段解鎖模式下車站追蹤間隔對比

從表2可以看出，采用進路分段鎖閉的策略后，間隔時間顯著縮短。且進路模式的改變，在微機聯鎖條件下是軟件的變化，成本相較提高列車動力性能要低，因此，為了縮小閉塞追蹤間隔，應該首先采用進路分段鎖閉模式。

5 結論

本文基于閉塞時間理論設計了移動閉塞追蹤間隔時間計算方法。在仿真系統中融入基于閉塞時間的計算列車追蹤間隔的算法，使仿真系統實現了對列車追蹤間隔的計算。對移動閉塞追蹤間隔時間計算方法中的列車長度、列車運行速度、列車牽引制動性能、進路鎖閉和解鎖方式等影響因素進行了實驗分析，得出了以下影響規律：當列車長度增大時，區間追蹤、車站發車及車站到達3種間隔時間均相應增大，且與短編組的追蹤間隔保持相同的趨勢；區間追蹤及車站到達間隔時間隨著速度降低基本呈線性關系下降，車站發車間隔時間并不隨限速的改變而改變；增大列車加速性能僅會影響列車車站出發間隔時間，增大列車制動性能會在很大程度上降低列車區間追蹤、車站通過及車站到達間隔時間，且呈現相同的下降趨勢和斜率；采用進路分段鎖閉策略較進路一次鎖閉間隔時間顯著縮短。