全向停車控制交叉口中行人與機動車延誤相互影響研究

溫豪杰，吳先宇， 袁振洲

(北京交通大學城市交通復雜系統理論與技術教育部重點實驗室，北京 100044)

交叉口作為城市道路網上的節點，是城市道路交通系統的咽喉。據統計，有80%的延誤發生在交叉口。因此，對交叉口進行延誤分析，可以準確地掌握交叉口的通行能力，為進一步評價城市道路以至整個路網的運行質量提供可靠的定量依據。而無信號交叉口作為最普通的交叉口類型之一，雖然其通行能力一般低于信號交叉口，但在路網交通控制中起著非常重要的作用。

針對無信號交叉口的延誤，國內外學者已經做了大量的研究工作。在行人過街延誤方面，國外較為成熟的研究成果有美國的HCM模型、澳大利亞的Virkler模型等[1]，北卡羅萊納州大學的Rouphail等在成群行人的可穿越間隙的基礎上建立了行人延誤模型，Ishaque等[3]用VISSIM對人車交互模型進行仿真，通過改變行人和車輛參數來矯正模型。國內的研究如馮樹民等[4]針對行人一次穿越一條車道和多條車道出現可穿越間隙下過街兩種情況，推算出行人過街平均延誤的計算方法；楊曉光等[5]以行人過街延誤為依據，建立了無信號控制下行人過街延誤計算模型；廖明軍等[6]研究了行人交通流的交通特性，討論了關于行人運動行為的內容以及相應的研究方法；李慶豐等[7]提出了一種新的人行橫道行人延誤的測量方法；張珩等[8]通過對中國行人過街行為的分析，建立了無信號交叉口行人從眾過街對交通流延誤的影響模型，反映了行人違章過街對交通流延誤造成的巨大影響。

在機動車通行能力和延誤方面的理論研究較為豐富。Tanner[9]基于可接受間隙理論，在交叉口主路車流優先的情形下假設主路車流車頭時距服從負指數分布，提出了一種計算支路通行能力的方法；隨后 Cowan[10]改進了負指數分布，給出當主路車流車頭時距服從M3分布時，支路通行能力的計算公式；李淑慶等[11]建立了無信號交叉口處左轉車流的通行能力模型;李文燕[12]基于間隙接受理論，對無信號T型交叉口的通行能力進行了建模仿真研究;王殿海等[13]改進了無信號交叉口的可插車間隙理論模型，假設直行車只有部分優先權，提出了兩相位交叉口處左轉車輛的通行能力計算模型，與傳統模型相比該模型誤差更小，計算結果更符合實際。

近年來，學者對于信號交叉口的人車沖突交互行為分析研究成果頗豐。曹更立等[14]基于機動車行駛安全性與舒適性，提出了信號交叉口展寬段及漸變段的計算模型；劉艷婷等[15]運用生存分析方法比較了信號交叉口行人與自行車等待忍耐時間的分布以及等待行為影響因素的異同；于瑞康等[16]分析了信號交叉口過街行人堆積與右轉機動車之間的沖突行為，得出了行人堆積數量與右轉機動車延誤之間強相關的結論。然而近期關于無信號控制交叉口人車交互的研究較少，且鮮有創新性的理論分析模型提出。

全向停車控制(all-way stop-controlled，AWSC)作為無信號交叉口的一種常用控制形式，要求交叉口的所有引道都設置停車標志，即所有引道上的駕駛員在進入交叉口前必須停車。駕駛員要根據道路規則(如右側駕駛員具有優先通行權)和其他引道的交通狀況決定是否前進。目前在一些區域的公認規則是給予右側駕駛員較高的優先權，但事實上規則的確立應當取決于交叉口的幾何線形以及車輛到達停車線的模式。

在國內外目前關于AWSC交叉口的研究中，多側重于機動車的通行能力、延誤以及行人延誤，而很少關注到行人過街延誤與機動車延誤之間的相互影響，并沒有去探索兩者之間的內在聯系。本文主要通過對某一典型AWSC交叉口的視頻數據進行處理，研究行人過街延誤與機動車延誤的相互關系，為更加準確地掌握無信號交叉口通行能力、進一步評價整個路網的運行質量提供可靠的依據。

1 研究區域

本文選取美國內華達州里諾市某AWSC交叉口為研究對象，該交叉口由東西向E 9thSt和南北向N Center St相交而成。其中東西向進口道分別只有一條車道，為直左右車道，略有展寬；南北向進口道分別有兩條車道，一條直右車道，一條左轉專用車道。人行橫道長度均為11 m(圖1)。

圖1 AWSC交叉口示意圖Fig.1 Diagram of the AWSC intersection

2 模型研究

2.1 AWSC交叉口沖突分析

鑒于時間和水平有限，本文只針對行人與機動車之間12類最基本沖突情形進行研究，如圖2所示，這些情形中，無其他沖突車流存在，且機動車在行人過街之前(或同時)已經在停車線前停車。

圖2 行人與機動車12類基本沖突情形Fig.2 The 12 types of conflicts between pedestrians and vehicles

對該研究區域AWSC交叉口視頻(1 h，16:00—17:00)進行數據統計。對于機動車，統計數據包括車輛數、轉向、到達交叉口時刻、到達隊首時刻以及出發時刻；對于行人，統計數據包括行人數、走向、到達人行橫道時刻、出發時刻、完成過街時刻。

結合視頻，從原始數據中找出符合以上12類基本沖突的行人-機動車沖突組合，并分別一一對應，形成沖突對。現摘錄部分數據如表1所示。

表1 行人-機動車沖突組合

2.2 行人與機動車延誤相互關系模型

當行人過街對機動車通過交叉口造成影響時，機動車的延誤由原本的停車時間(沒有行人時)、行人延誤時間和行人過街時間三部分組成[17]。

2.2.1 行人半過街模型

圖3 行人半過街情形示意圖Fig.3 The situation of pedestrians crossing halfway

在圖2中的情形1、2、3、10、11、12中，機動車在行人過街完成一半時即可通行。雖然不符合全向停車控制交叉口過街規則，即要求待行人完全過街后機動車方可通過，但結合當地駕駛人員習慣，這種情形發生較為普遍。與此同時，通過視頻觀測可以發現，當機動車駕駛員按照AWSC交叉口通行規則停車后，若發現尚未到達人行橫道的行人有過街意圖，一般會在停車線前繼續停車等待，直至行人過街完成一半，即如圖3所示，當機動車停車時，行人到達位置①，此時機動車繼續等待；當行人到達位置②時，可能會對機動車是否前進做出判斷，判斷時間即為行人延誤；判斷完畢后行人開始過街，到達位置③時過街完成一半，此時行人不再對機動車通行造成影響，機動車可以啟動。

因此，行人半過街情形下，行人與機動車延誤相互關系模型可建立如下：

(1)

(2)

式中，Dv為機動車延誤，s；Dp為行人延誤，s；d為行人距離人行橫道的距離，m；L為人行橫道長度，m；v為行人走行速度，m/s；C1為無行人時機動車的停車時間，s，經計算約為1.8 s。

2.2.2 行人完全過街情形

圖4 行人完全過街情形示意圖Fig.4 The situation of pedestrians crossing completely

圖2中的情形4 ～ 9，機動車必須在行人完全過街后才能通行，即如圖4所示，當機動車停車時，行人到達位置①，此時機動車繼續等待；當行人到達位置②時，可能會對機動車是否前進做出判斷，判斷時間即為行人延誤；判斷完畢后行人開始過街，到達位置③時過街全部完成，此時行人不再對機動車通行造成影響，機動車可以啟動。

因此，與行人半過街情形同理可得行人完全過街情形下，行人與機動車延誤相互關系模型可建立如下：

(3)

其中，C2為無行人時機動車的停車時間，C2=C1，約為1.8 s。

2.3 行人與機動車延誤相互關系模型評價

本文采用實地交叉口數據以及交通軟件仿真獲取的仿真數據，進行對模型的驗證評價。

2.3.1 實地調研數據驗證

(1)半過街情形

將模型計算出的延誤與視頻統計的實際延誤對比，對模型進行驗證，見表2。

表2 半過街情形模型延誤與實際延誤對比Table 2 Comparison of delay between the halfway crossing model and actual situation

續表2

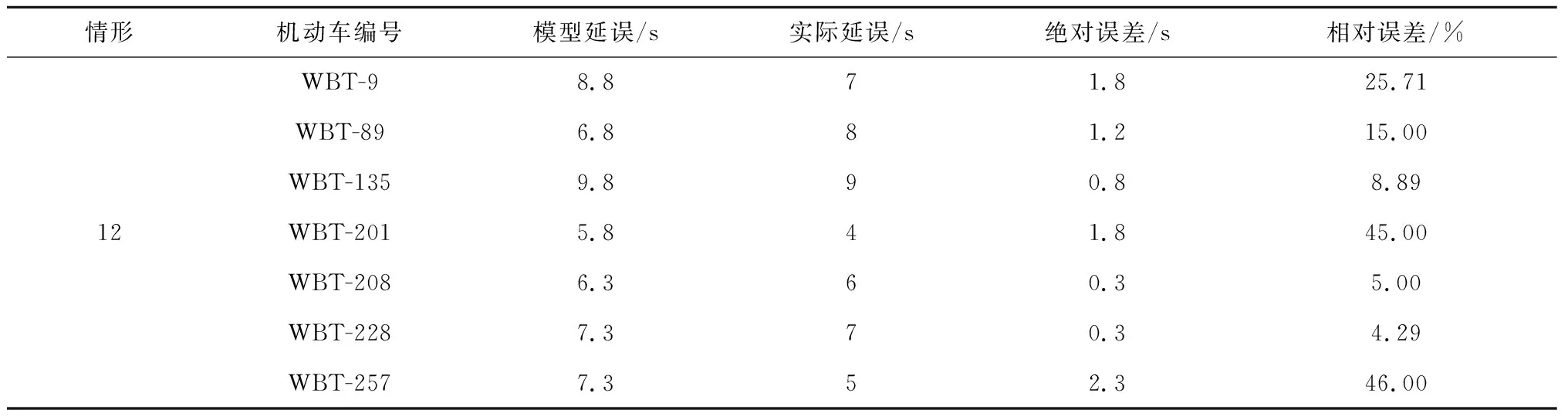
情形機動車編號模型延誤/s實際延誤/s絕對誤差/s相對誤差/%WBT-98.871.825.71WBT-896.881.215.00WBT-1359.890.88.8912WBT-2015.841.845.00WBT-2086.360.35.00WBT-2287.370.34.29WBT-2577.352.346.00

從表2可知，有21組數據的相對誤差≤20%，有8組數據的相對誤差>20%。按照相對誤差低于20%為擬合標準，行人半過街模型情形的29組數據中有21組數據符合標準，符合率為72.4%。

模型對過街情形1、2、3擬合情況較好，并沒有出現誤差大于20%的情形，誤差較大的情況均出現于過街情形為10、11、12的場景。對比情形1、2、3與情形10、11、12，發現前者場景的人車交互距離較近，可見在近距離情況下，機動車與行人延誤接近理論模型的預測值。而當人車交互距離較遠時，位置不確定性的增加使得駕駛員與行人之間心理博弈造成的隨機性增加，因此這部分數據中有部分樣本誤差較大，無法較好擬合模型。同時，部分機動車在可以實現半過街的情形中依舊選擇等待行人完成過街后再前進，這種在半過街情形中機動車啟動時間的不確定性也大大增加了誤差，這部分誤差是當前模型無法去擬合的。

(2)完全過街情形

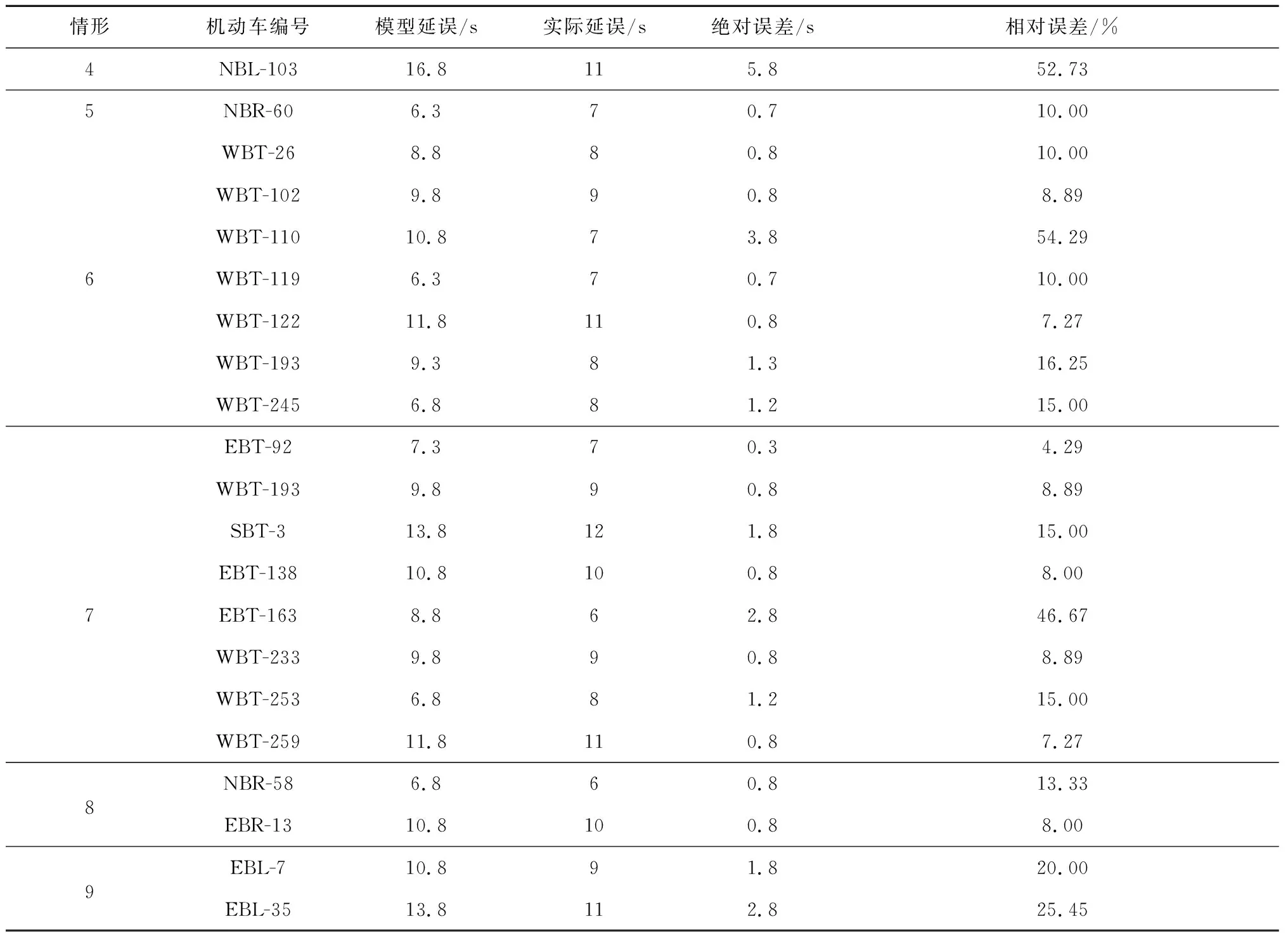
表3 完全過街情形模型延誤與實際延誤對比Table 3 Comparison of delay between the crossing completely model and actual situation

從表3可知，有17組數據的相對誤差≤20%，有4組數據的相對誤差>20%。行人完全過街情形的21組數據中有17組數據符合標準，符合率為81.0%。

模型可以擬合的樣本數量超過80%，擬合效果較好。誤差較大的4組數據在情形4、6、7、9中各有一例。通過對視頻研究發現，由于這幾種情形下行人和機動車交互距離較遠，而且根據觀察，有部分機動車未遵守AWSC規則，在行人過街前通過交叉口，使部分樣本真實延誤與模型計算結果存在一定誤差。

(3)模型驗證結論

從驗證結果總體來看，建立的理論模型從很大程度上解釋了AWSC交叉口機動車與行人延誤之間的關系，擬合效果較好。人半過街和完全過街情形下的行人與機動車延誤相互關系模型由于時間和水平有限，還存在一定的誤差，有待完善，但同時也為進一步的研究提供了新思路。

2.3.2 仿真驗證

Synchro是一款由美國Trafficware公司根據美國交通部標準HCM研發的一款交通配時優化軟件，同時具備通行能力仿真功能，其仿真特性較為符合美國出行習慣。本文利用Synchro軟件對行人與機動車延誤相互關系模型進行評價，通過建立交叉口、車道和流量等參數設置，在完成設置后輸出仿真結果，部分結果如表4所示。

表4 仿真結果

從仿真結果來看，各個進口道的仿真延誤和實際延誤有很大差異。這是由于Synchro內部并沒有針對AWSC交叉口規則制定的仿真過程。

事實上，目前并沒有交通軟件能對此類交叉口做相應的仿真。因此，目前無法利用現有仿真軟件對模型進行準確地評價，只能通過實測數據與模型計算結果對比來驗證模型準確性。但這為進一步的相關研究提供了方向：通過編程方法建立符合AWSC交叉口規則的仿真模型用以日后的相關研究。

3 結論

交叉口是道路網絡中的關鍵節點，更是交通瓶頸和交通事故的多發點。因此，必須依靠先進的交通管理和控制措施來解決交叉口問題，減少交通延誤，提高交叉口通行能力，以適應日益增長的交通需求，從而保證城市交通的安全與暢通。本文在全面了解國內外無信號交叉口研究現狀的基礎上，利用美國里諾市某AWSC交叉口的視頻數據，全面分析了AWSC交叉口中行人與機動車的基本沖突情形，總結出12類基本沖突情形，并將這些基本沖突劃分為行人半過街和完全過街兩種情況分別進行理論分析建模，并利用現有數據對模型進行驗證分析，取得了一定的效果，但是受限于研究時間和個人精力，本研究存在以下不足：

(1)本次研究局限于美國的一個AWSC交叉口，未能對更多同類交叉口進行類比研究分析。

(2)本次研究僅針對行人與機動車12類最基本的沖突情形，未能考慮有多名不同走向行人、多輛機動車時，行人與機動車之間的相互影響。

(3)所建模型受樣本量限制，準確度不高。雖然根據交叉口視頻統計了3 000多個數據，但真正能夠用于驗證模型的樣本數量仍然較少。

目前我國對于無信號交叉口的研究較為局限，全向停車控制交叉口在國內則更是鮮見。實際上，對于車流量較小的一些城市道路交叉口，設置信號燈只會增大交叉口延誤，理應采取無信號控制方式，而停車控制作為無信號控制方式的一種，在減少延誤的前提下還在一定程度上降低了機動車通過交叉口的速度，給行人過街創造了有利條件，同時也大大降低了交通事故的發生概率。除了加大推廣應用以外，早日建立完備的無信號口相關法律法規也是至關重要的。只有行人、機動車遵循相應的交通規則，交叉口才能充分發揮其通行能力，才能更安全更快捷地為人們的出行提供服務。