基于傾向得分多層模型的非概率抽樣統(tǒng)計(jì)推斷
劉 展
(湖北大學(xué)a.數(shù)學(xué)與統(tǒng)計(jì)學(xué)學(xué)院;b.應(yīng)用數(shù)學(xué)湖北省重點(diǎn)實(shí)驗(yàn)室,武漢430062)
0 引言
網(wǎng)絡(luò)調(diào)查由于其具有比電話調(diào)查更短的數(shù)據(jù)收集周期和更低的費(fèi)用而急劇增長,目前已經(jīng)在市場(chǎng)研究的調(diào)查數(shù)據(jù)收集中占主導(dǎo)地位。網(wǎng)絡(luò)調(diào)查可視為一種單一的模式,但其抽取樣本的方法有多種,包括基于概率抽樣的網(wǎng)絡(luò)調(diào)查與基于非概率抽樣的網(wǎng)絡(luò)調(diào)查,其中最值得注意的是基于非概率抽樣的候選者數(shù)據(jù)庫網(wǎng)絡(luò)調(diào)查。這里網(wǎng)絡(luò)調(diào)查的候選者數(shù)據(jù)庫,簡稱網(wǎng)絡(luò)候選者數(shù)據(jù)庫,指自愿完成網(wǎng)絡(luò)調(diào)查的上網(wǎng)人群,如果在后續(xù)的網(wǎng)絡(luò)調(diào)查中選擇他們作為調(diào)查對(duì)象,他們將配合完成調(diào)查[1]。候選者數(shù)據(jù)庫網(wǎng)絡(luò)調(diào)查是從網(wǎng)絡(luò)候選者數(shù)據(jù)庫中抽取樣本進(jìn)行網(wǎng)絡(luò)調(diào)查,其獲得的樣本為網(wǎng)絡(luò)候選者數(shù)據(jù)庫的調(diào)查樣本。可以看到,候選者數(shù)據(jù)庫網(wǎng)絡(luò)調(diào)查本質(zhì)上屬于非概率抽樣調(diào)查,其樣本屬于非概率樣本,入樣概率未知,采用傳統(tǒng)的抽樣推斷理論進(jìn)行推斷存在一定的困難。因此,非概率樣本的統(tǒng)計(jì)推斷問題,特別是候選者數(shù)據(jù)庫網(wǎng)絡(luò)調(diào)查的推斷問題,就成為網(wǎng)絡(luò)調(diào)查發(fā)展中迫切需要解決的問題。
傾向得分調(diào)整方法是一種被廣泛應(yīng)用于非概率抽樣推斷的方法。Duncan和Stasny(2001)[2]利用傾向得分方法降低了電話調(diào)查的覆蓋偏差。Schonlau等(2004)[3]與Lee(2006)[4]指出傾向得分調(diào)整方法可能有助于減少抽樣框覆蓋不全、無回答、非概率抽樣等產(chǎn)生的偏差。Brick(2013)[5]提出使用傾向得分加權(quán)來解決單元無回答的缺失問題。Schonlau 等(2009)[6]將性別、年齡、教育、收入等作為X,是否上網(wǎng)作為Y建立模型,構(gòu)建非概率樣本的傾向得分權(quán)數(shù),最終得到的加權(quán)估計(jì)接近于總體參數(shù)真值。Valliant和Dever(2011)[7]結(jié)合網(wǎng)絡(luò)候選者數(shù)據(jù)庫和參考樣本,建立logistic回歸模型來估計(jì)傾向得分,并基于傾向得分對(duì)非概率樣本構(gòu)造了不同的權(quán)數(shù)來估計(jì)總體。然而,以上建立傾向得分模型估計(jì)傾向得分來推斷總體均是在單一層次數(shù)據(jù)背景下進(jìn)行的,即假設(shè)網(wǎng)絡(luò)候選者數(shù)據(jù)庫的數(shù)據(jù)結(jié)構(gòu)是單一層次的,然而在一些情況下網(wǎng)絡(luò)候選者數(shù)據(jù)庫的數(shù)據(jù)結(jié)構(gòu)可能是多層次或嵌套結(jié)構(gòu)。多層次或嵌套結(jié)構(gòu)就是在上一級(jí)分層的基礎(chǔ)上進(jìn)行再分層,形成一層套一層的嵌套結(jié)構(gòu)或多層次結(jié)構(gòu),單一層次結(jié)構(gòu)就是一個(gè)層次,不再逐層細(xì)分。例如,學(xué)生往往在一個(gè)班級(jí)內(nèi)可以被分成不同的類,反過來這些班級(jí)又在學(xué)校內(nèi)可以被分成不同的群。如果忽略數(shù)據(jù)的嵌套結(jié)構(gòu),仍然采用單一層次結(jié)構(gòu)下的方法進(jìn)行分析,可能會(huì)導(dǎo)致誤導(dǎo)性或不準(zhǔn)確的結(jié)果。因此,當(dāng)網(wǎng)絡(luò)候選者數(shù)據(jù)庫數(shù)據(jù)具有嵌套結(jié)構(gòu)時(shí),需要考慮針對(duì)嵌套結(jié)構(gòu)數(shù)據(jù)的傾向得分估計(jì)方法。Li等(2013)[8]在觀察性研究中針對(duì)多層(嵌套)結(jié)構(gòu)數(shù)據(jù),探究了建立多層模型估計(jì)傾向得分來估計(jì)平均處理效應(yīng),但是并未探討總體推斷的問題。關(guān)于多層模型在醫(yī)療護(hù)理、衛(wèi)生政策、教育等諸多領(lǐng)域中的應(yīng)用研究文獻(xiàn)越來越多,同時(shí)傾向得分分析也日益流行,然而對(duì)多層次數(shù)據(jù)結(jié)構(gòu)的傾向得分分析還沒有得到深入的研究。基于此,本文針對(duì)具有嵌套結(jié)構(gòu)數(shù)據(jù)的網(wǎng)絡(luò)候選者數(shù)據(jù)庫和參考樣本,探索構(gòu)建傾向得分多層模型來推斷總體的方法。為了便于討論,本文主要考慮兩個(gè)層次的嵌套結(jié)構(gòu)數(shù)據(jù)。
1 多層模型
多層模型(Multilevel Modeling,簡記為MLM)是包含固定效應(yīng)和(或)隨機(jī)效應(yīng)的回歸模型,是一種用于評(píng)價(jià)嵌套結(jié)構(gòu)數(shù)據(jù)的統(tǒng)計(jì)分析方法[9]。多層模型是通過解釋單元間的依賴關(guān)系、適當(dāng)調(diào)整標(biāo)準(zhǔn)誤差、在所有層次上分解方差,來改進(jìn)嵌套數(shù)據(jù)中個(gè)體效應(yīng)的估計(jì)。此外,多層模型允許跨層次的相互作用,這種相互作用解釋了在一個(gè)層次測(cè)量的變量是如何影響在另一層次上所發(fā)生的關(guān)聯(lián)的[9]。換句話說,對(duì)嵌套數(shù)據(jù)建立多層模型允許研究者去調(diào)查結(jié)果的變動(dòng)有多少與群內(nèi)和群間個(gè)體之間的差異有關(guān)[10]。下面討論具體的多層模型方程。
對(duì)第j個(gè)群中第i個(gè)人觀測(cè)的連續(xù)因變量Y的多層模型如下:
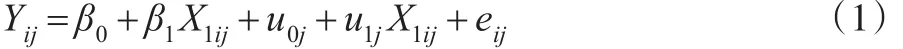
式(1)中β0、β1是固定效應(yīng),u0j、u1j為隨機(jī)效應(yīng),eij為隨機(jī)誤差項(xiàng)。其中固定效應(yīng)是未知的常數(shù)(參數(shù)),定義了預(yù)測(cè)變量X1ij與因變量Yij之間的關(guān)系;隨機(jī)效應(yīng)是隨機(jī)變量,允許回歸模型中的系數(shù)根據(jù)研究的群或個(gè)體(對(duì)象)隨機(jī)變動(dòng),因此多層模型也稱為隨機(jī)系數(shù)模型。既然隨機(jī)效應(yīng)是隨機(jī)變量,相應(yīng)的就需要對(duì)隨機(jī)效應(yīng)定義概率分布,這就意味著多層模型比一般的回歸模型有更多的參數(shù)需要估計(jì)。隨機(jī)效應(yīng)與隨機(jī)誤差項(xiàng)通常的假定分布為:
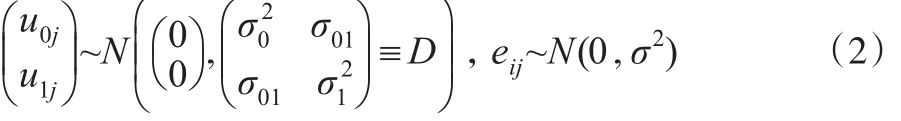
其中D為隨機(jī)效應(yīng)的方差協(xié)方差矩陣,為u0j的方差,為u1j的方差,σ01為u0j與u1j的協(xié)方差,σ2為eij的方差。
事實(shí)上,多層模型(1)也可以寫成另外一種形式,如式(3)所示,式(3)是更為常見的一種形式,很多軟件比如HLM、MLwiN等使用的都是這種形式。
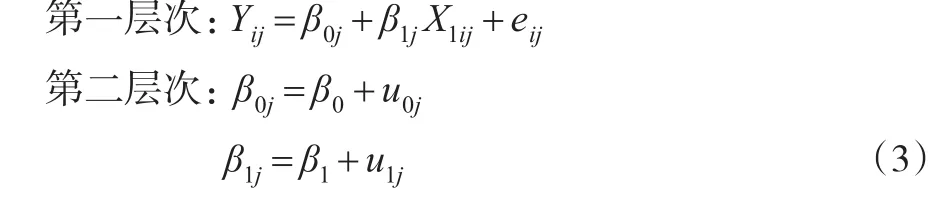
其中β0j、β1j為隨機(jī)系數(shù),并且β0j為第一層次方程的截距,β1j為第一層次方程的斜率,將第一層次與第二層次的方程結(jié)合即可得到式(1),第二層次中關(guān)于β0j的方程稱為截距方程,關(guān)于β1j的方程稱為斜率方程。式(3)清晰地定義了多層模型中第二層次所測(cè)量的第一層次預(yù)測(cè)變量,可以將第二層次的每個(gè)隨機(jī)系數(shù)方程視為一個(gè)僅有截距項(xiàng)的回歸模型,并且可以通過在這個(gè)模型中增加第二層次預(yù)測(cè)變量來解釋隨機(jī)效應(yīng)的方差,比如在截距方程中增加性別Gender作為第二層次預(yù)測(cè)變量,則β0j=β0+β2Genderj+u0j,β2為未知常數(shù)(固定效應(yīng))。
式(3)只是一個(gè)簡單的二層次模型,在具體建模時(shí)可根據(jù)具體的問題在第一層次方程中添加預(yù)測(cè)變量如X2ij,…,Xpij等,在第二層次方程中也可以添加一些預(yù)測(cè)變量。總之,在多層模型中預(yù)測(cè)變量可以被添加到第一層次和第二層次的模型方程中,這些變量的截距或斜率可以跨層次的變動(dòng),即截距或斜率可以為隨機(jī)變量,是否限制或允許第一層次與第二層次預(yù)測(cè)變量跨層次變動(dòng)是多層模型特殊的一個(gè)重要方面[9,11,12]。如果為三層次模型,則第二層次方程中的一些系數(shù)也是隨機(jī)的,可以同樣寫出隨機(jī)系數(shù)的第三層次方程,依次可類推到多個(gè)層次的模型。
對(duì)于多層模型的估計(jì),可以從矩陣形式來考慮。在隨機(jī)效應(yīng)的條件下,第 j個(gè)對(duì)象或群的觀測(cè)向量分布為 Yj|uj~N(Xjβ+Zjuj,Rj),其中Xj為預(yù)測(cè)變量設(shè)計(jì)矩陣,β為固定效應(yīng)向量,Zj為更小一些的預(yù)測(cè)變量設(shè)計(jì)矩陣,uj為隨機(jī)效應(yīng)向量,Rj為隨機(jī)誤差的方差協(xié)方差矩陣。所有隨機(jī)效應(yīng)平均下Y的邊際分布為Vj),其中Xjβ為第j個(gè)對(duì)象或群的觀測(cè)Y的期望向量,D為隨機(jī)效應(yīng)的方差協(xié)方差矩陣對(duì)象或群的觀測(cè)Y的邊際方差協(xié)方差矩陣。在此基礎(chǔ)上,采用某種形式的極大似然估計(jì)方法來估計(jì)模型參數(shù)。假設(shè)對(duì)象或群是相互獨(dú)立的,首先寫出似然函數(shù)形式為的邊際概率密度函數(shù),β、θ為待估參數(shù),對(duì)有些模型來說似然函數(shù)可能需要近似。然后,使用迭代數(shù)學(xué)方法(比如Newton-Raphson)找到使得(近似的)似然函數(shù)值達(dá)到最大的模型參數(shù)估計(jì)。
2 傾向得分多層模型及總體估計(jì)
假設(shè)網(wǎng)絡(luò)候選者數(shù)據(jù)庫的協(xié)變量數(shù)據(jù)具有嵌套結(jié)構(gòu),比如協(xié)變量包括了班級(jí)、學(xué)校等變量,此時(shí)網(wǎng)絡(luò)候選者數(shù)據(jù)庫單元為不同學(xué)校不同班級(jí)里的學(xué)生。從該網(wǎng)絡(luò)候選者數(shù)據(jù)庫中隨機(jī)抽取一個(gè)樣本進(jìn)行調(diào)查,得到一個(gè)網(wǎng)絡(luò)候選者數(shù)據(jù)庫的調(diào)查樣本;同時(shí)假設(shè)獲得了另一個(gè)具有同樣嵌套結(jié)構(gòu)數(shù)據(jù)的參考樣本,比如采用多階段隨機(jī)抽樣得到了另一個(gè)概率樣本。設(shè)調(diào)查樣本中第j個(gè)群第i個(gè)單元的入樣概率 πij=π(Xij),Xij=(Xij1,Xij2,…,Xijp)′是協(xié)向量,p是協(xié)變量數(shù)目,則有:
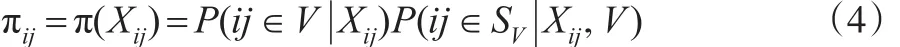
其中,V是網(wǎng)絡(luò)候選者數(shù)據(jù)庫;SV是從網(wǎng)絡(luò)候選者數(shù)據(jù)庫中隨機(jī)抽取的調(diào)查樣本;P(i j ∈ SV|Xij,V)是網(wǎng)絡(luò)候選者數(shù)據(jù)庫中第j個(gè)群第i個(gè)單元進(jìn)入網(wǎng)絡(luò)調(diào)查樣本的概率,常常已知;P(ij∈V|Xij)是第j個(gè)群第i個(gè)單元自愿加入網(wǎng)絡(luò)候選者數(shù)據(jù)庫的概率,往往未知需要估計(jì)。設(shè)示性變量D表示單元是否加入網(wǎng)絡(luò)候選者數(shù)據(jù)庫,D=1記為單元加入網(wǎng)絡(luò)候選者數(shù)據(jù)庫,D=0記為單元未加入網(wǎng)絡(luò)候選者數(shù)據(jù)庫,那么第 j個(gè)群第i個(gè)單元加入網(wǎng)絡(luò)候選者數(shù)據(jù)庫的概率就是p(Xij)=P(Dij=1|Xij)=P(ij∈V|Xij)。
根據(jù)傾向得分的定義:給定輔助變量X的條件下單元接受處理(參與或回答)的條件概率,可知p(Xij)=P(ij∈V|Xij)本質(zhì)上就是傾向得分。由于p(Xij)為一個(gè)概率,其范圍在0到1之間,取值有限,直接建立多層模型不太合適,因此考慮使用聯(lián)結(jié)函數(shù),如最常用的Logit聯(lián)結(jié),即logit(p(Xij))=log(p(Xij)(1-p(Xij))),將概率范圍(0,1)轉(zhuǎn)換為(-∞,∞),再建立多層模型。在建立多層模型時(shí),有很多的模型選擇,比如第一層次的預(yù)測(cè)變量可以假定在群層次(第二層次)上是固定的或變動(dòng)的;第二層次的預(yù)測(cè)變量可以僅包含在截距方程中,僅影響截距,也可以既包含在截距方程中,也包含在斜率方程中,同時(shí)影響截距和斜率。總之,在模型假定上進(jìn)行不同層次預(yù)測(cè)變量的添減以及截距、斜率隨機(jī)性的設(shè)置,就會(huì)產(chǎn)生許多不同的多層模型。下面分別進(jìn)行討論。
(1)具有固定斜率隨機(jī)截距且不包含第二層次預(yù)測(cè)變量的傾向得分多層模型。
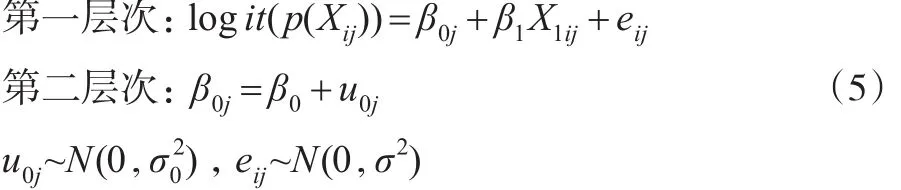
這里logit(p(Xij))表示傾向得分的Logit函數(shù);β0為斜率方程中的斜率(固定);β1為第一層次方程中的斜率(固定)。該模型假定不同群中X1與logit(p(Xij))回歸方程的斜率相同截距不同,截距不同是由群的差異所引起的,但并未考慮群層次上具體變量對(duì)截距的影響。此模型通過固定斜率,假定X1對(duì)logit(p(Xij))的影響在不同群中是一樣的。
(2)具有固定斜率隨機(jī)截距且包含第二層次預(yù)測(cè)變量的傾向得分多層模型。
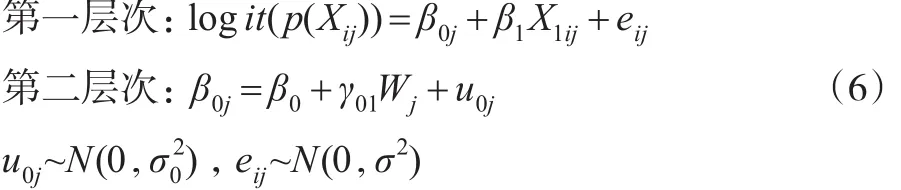
其中Wj為第二層次上的預(yù)測(cè)變量,γ01為固定斜率。此模型假定第二層次預(yù)測(cè)變量W只對(duì)X1與logit(p(Xij))回歸方程的截距產(chǎn)生影響,換句話說不同群中X1與logit(p(Xij))回歸方程的截距不同斜率相同,截距受到預(yù)測(cè)變量W的影響。
(3)具有隨機(jī)斜率固定截距且不包含第二層次預(yù)測(cè)變量的傾向得分多層模型。
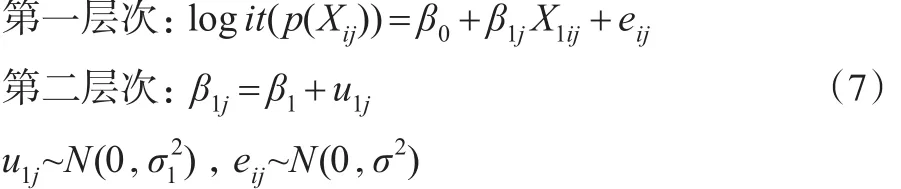
此模型假定不同群中X1與logit(p(Xij))回歸方程的截距相同斜率不同,斜率不同是由群的差異所引起的,但并未考慮群層次上具體變量對(duì)斜率的影響。
(4)具有隨機(jī)斜率固定截距且包含第二層次預(yù)測(cè)變量的傾向得分多層模型。
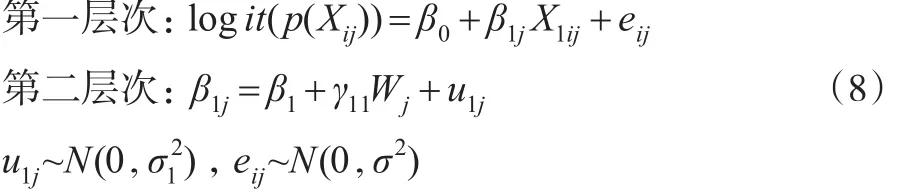
其中Wj為第二層次上的預(yù)測(cè)變量,γ11為固定斜率。此模型假定不同群中X1與logit(p(Xij))回歸方程的斜率不同截距相同,斜率受到預(yù)測(cè)變量W的影響,即第二層次預(yù)測(cè)變量W對(duì)第一層次預(yù)測(cè)變量與因變量之間的關(guān)系產(chǎn)生影響。
(5)具有隨機(jī)斜率隨機(jī)截距且均不包含第二層次預(yù)測(cè)變量的傾向得分多層模型。
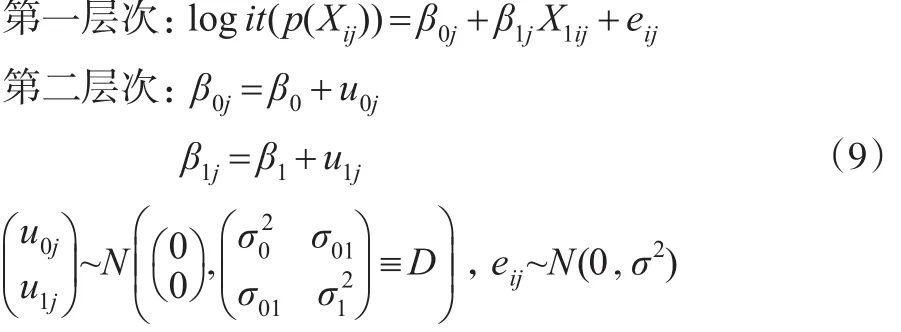
此模型假定不同群中X1與logit(p(Xij))回歸方程的截距和斜率均不同,截距和斜率的不同是由群的差異所引起的,但并未考慮群層次上具體變量對(duì)截距和斜率的影響。
(6)具有隨機(jī)斜率與截距且均包含第二層次預(yù)測(cè)變量的傾向得分多層模型。
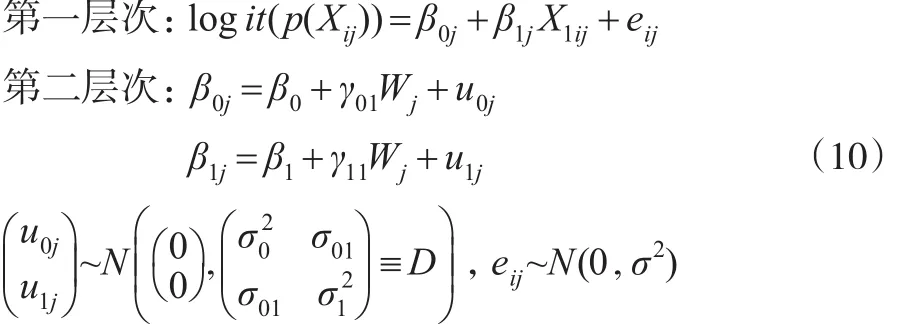
其中γ01為截距方程中預(yù)測(cè)變量固定的斜率,γ11為斜率方程中預(yù)測(cè)變量固定的斜率。此模型假定預(yù)測(cè)變量W對(duì)不同群中X1與logit(p(Xij))回歸方程的截距和斜率都產(chǎn)生影響。
(7)具有隨機(jī)斜率與截距且截距斜率其中之一包含第二層次預(yù)測(cè)變量的傾向得分多層模型。
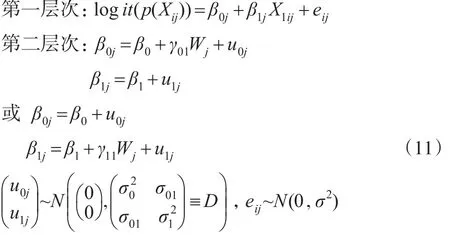
此模型假定預(yù)測(cè)變量W對(duì)不同群中X1與logit(p(Xij))回歸方程的截距或斜率產(chǎn)生影響。以上只是考慮了第一層、第二層中一個(gè)預(yù)測(cè)變量的情形,可以根據(jù)具體的情況,添加多個(gè)預(yù)測(cè)變量。
在建立傾向得分多層模型之后,可以估計(jì)出logit(p(Xij)),得到傾向得分的估計(jì)帶入式(4)則得到 πij的估計(jì)值,即:
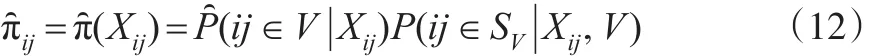
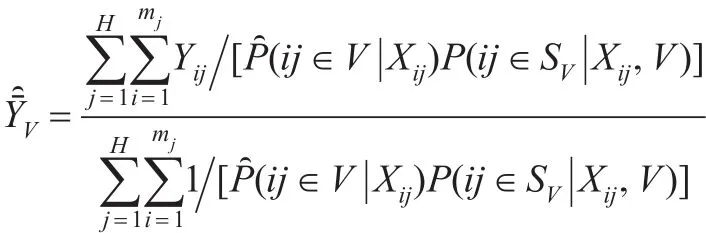
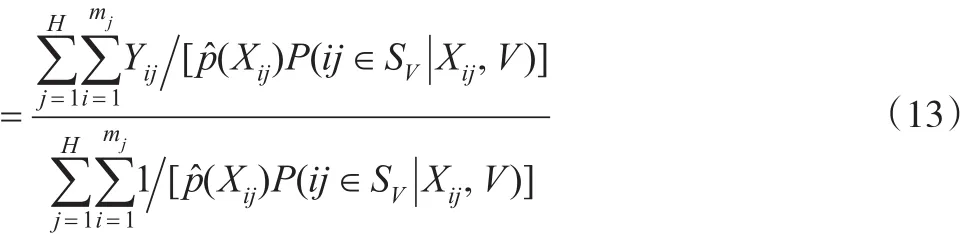
其中網(wǎng)絡(luò)候選者數(shù)據(jù)庫的調(diào)查樣本SV可分成H個(gè)群(第二層次),第j個(gè)群包含mj個(gè)個(gè)體(第一層次),j=1,…,H。如果總體規(guī)模N已知時(shí),可將式(13)的分母換為N。該加權(quán)調(diào)整方法可稱為傾向得分逆加權(quán)方法。此外,對(duì)總體均值估計(jì)的方差可使用重抽樣方法,如Bootstrap、Jackknife等來進(jìn)行估計(jì)。
3 模擬研究
現(xiàn)對(duì)本文所提出的總體估計(jì)方法的效果進(jìn)行模擬研究。首先生成一個(gè)大小為100000(N=100000)的具有嵌套數(shù)據(jù)結(jié)構(gòu)的有限總體,協(xié)變量(預(yù)測(cè)變量)包括個(gè)體層次(第一層次)上服從正態(tài)分布N(1,1)的變量X以及群層次(第二層次)上服從正態(tài)分布N(0,1)的變量W,群個(gè)數(shù)m為50,每個(gè)群包含的個(gè)體單元數(shù)都相等為Nm=2000,目標(biāo)變量Y值由兩個(gè)協(xié)變量X、W以及多層線性模型Y=-0.5+0.5X-0.4W+0.3W×X+u1X+u0+ε來生成,其中u0、u1與ε分別由以下分布來產(chǎn)生:
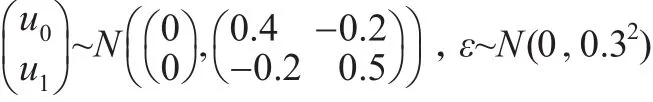
在生成的有限總體中不放回簡單隨機(jī)抽取20個(gè)群(每個(gè)群2000個(gè)單元),然后在每個(gè)群中不放回簡單隨機(jī)抽取50個(gè)單元,得到樣本量為1000(nr=1000)的一個(gè)樣本,視其為參考樣本。然后,從20個(gè)群共40000個(gè)單元中去掉參考樣本單元后的剩余單元中,再分別從20個(gè)群中不放回簡單隨機(jī)抽取1000個(gè)單元,得到一個(gè)有20個(gè)群且每個(gè)群包含1000個(gè)單元的嵌套樣本,將其作為網(wǎng)絡(luò)候選者數(shù)據(jù)庫V,規(guī)模為M=20000。接著,采取分層隨機(jī)抽樣從網(wǎng)絡(luò)候選者數(shù)據(jù)庫V的20個(gè)群中不放回簡單隨機(jī)抽取500個(gè)單元,作為網(wǎng)絡(luò)候選者數(shù)據(jù)庫的調(diào)查樣本SV,樣本量為10000(nv=10000)。將上面的過程重復(fù)1000次,獲得1000組蒙特卡羅樣本,針對(duì)每一組樣本構(gòu)建具有隨機(jī)斜率與截距且均包含第二層次預(yù)測(cè)變量的傾向得分多層模型以及單一層次結(jié)構(gòu)下的Logistic傾向得分模型(忽略數(shù)據(jù)的嵌套結(jié)構(gòu))來估計(jì)傾向得分,并采用傾向得分逆加權(quán)方法來估計(jì)總體均值。這里的Logistic傾向得分模型為:

其中Xij=(Xij1,Xij2,…,Xijp)′為協(xié)向量,p為協(xié)變量個(gè)數(shù),β為回歸參數(shù)。最后,計(jì)算1000組模擬樣本上總體估計(jì)的均值、方差、偏差與均方誤差。

表1 基于傾向得分多層模型的總體均值估計(jì)的模擬結(jié)果
表1為基于傾向得分多層模型和Logistic模型并使用傾向得分逆加權(quán)調(diào)整方法計(jì)算的總體估計(jì)的均值、方差、偏差與均方誤差。兩種方法估計(jì)的總體均值較為接近,且總體均值估計(jì)的方差基本相同。從偏差上看傾向得分多層模型的逆加權(quán)估計(jì)偏差相對(duì)來說更小,而兩種方法估計(jì)的總體均值的均方誤差一樣,說明對(duì)于具有嵌套數(shù)據(jù)結(jié)構(gòu)的網(wǎng)絡(luò)候選者數(shù)據(jù)庫,基于傾向得分多層模型的總體估計(jì)相對(duì)于基于傾向得分Logistic模型的總體估計(jì)偏差更小,無偏程度更高,而兩個(gè)估計(jì)的效率基本一樣。
4 實(shí)證分析
實(shí)證數(shù)據(jù)來自2014年美國綜合社會(huì)調(diào)查(General Social Survey,簡記為GSS),選取調(diào)查中的性別(gender)、年齡(age)、種族(race)、區(qū)域(region)、教育(education)、收入(income)和投票變量(vote12)共7個(gè)變量,2538個(gè)個(gè)案的一個(gè)數(shù)據(jù)集,其中區(qū)域變量為群的分類變量,共分9個(gè)群。因?yàn)閿?shù)據(jù)中出現(xiàn)了“不知道(Don't know)”、“無回答(No answer)”、“不適用(Not applicable)”、“不合格(Ineligible)”等選擇結(jié)果,所以本文將這些結(jié)果的個(gè)案刪除。此外,為了簡化計(jì)算進(jìn)一步對(duì)變量值進(jìn)行了一些變換,獲得7個(gè)變量、191個(gè)單元的最終數(shù)據(jù)集,7個(gè)變量的類型與具體取值見表2。
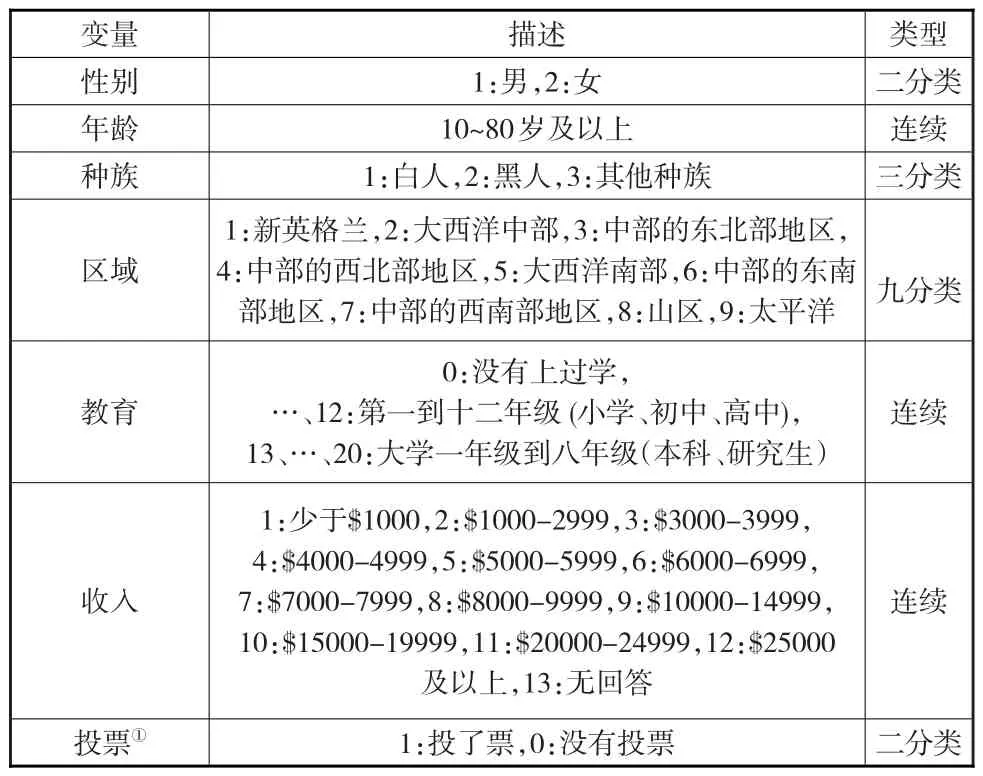
表2 基于傾向得分多層模型推斷的實(shí)證變量
由于多層模型需要較多的數(shù)據(jù),因此本文首先利用Bootstrap來構(gòu)造一個(gè)偽總體。具體地,使用有放回簡單隨機(jī)抽樣方法,從191個(gè)單元中抽取一個(gè)大小為100的樣本,重復(fù)抽取100次,獲得10000個(gè)單元,將這10000個(gè)單元和191個(gè)單元匯總,從而形成一個(gè)大小為10191的偽總體(N=10191)。然后,先使用PPS抽樣從偽總體中抽取7個(gè)群即7個(gè)區(qū)域,再在每個(gè)區(qū)域中不放回簡單隨機(jī)抽取20個(gè)單元,得到一個(gè)大小為140的參考樣本(概率樣本,nr=140)。接著,從7個(gè)區(qū)域中去掉參考樣本單元之后,再分別從每個(gè)區(qū)域不放回簡單隨機(jī)抽取300個(gè)單元作為網(wǎng)絡(luò)候選者數(shù)據(jù)庫V(規(guī)模為M=2100)。進(jìn)一步從網(wǎng)絡(luò)候選者數(shù)據(jù)庫的每個(gè)區(qū)域中不放回簡單隨機(jī)抽取一個(gè)樣本量為100的樣本,即網(wǎng)絡(luò)候選者數(shù)據(jù)庫的調(diào)查樣本SV(nv=700)。在偽總體固定的情況下,重復(fù)抽取參考樣本和網(wǎng)絡(luò)候選者數(shù)據(jù)庫的調(diào)查樣本1000次。
現(xiàn)對(duì)2012年總統(tǒng)選舉中投票人數(shù)所占的比例,即投票變量Yvote的均值進(jìn)行估計(jì),將年齡、性別、種族、教育、收入作為投票個(gè)體(第一層次)上的協(xié)變量,并且投票的個(gè)體嵌套于區(qū)域?qū)哟危ǖ诙哟危┲小T?000組參考樣本與網(wǎng)絡(luò)候選者數(shù)據(jù)庫的調(diào)查樣本上,建立具有固定斜率隨機(jī)截距且不包含第二層次預(yù)測(cè)變量的傾向得分多層模型以及Logistic傾向得分模型來估計(jì)傾向得分,并將傾向得分的逆作為權(quán)數(shù)進(jìn)行加權(quán)調(diào)整來估計(jì)投票人數(shù)所占的比例。最后,計(jì)算1000組樣本上總體估計(jì)的均值、方差、偏差與均方誤差,見表3。

表3 基于傾向得分多層模型的總體均值估計(jì)的實(shí)證結(jié)果
由表3可知,建立傾向得分多層模型與Logistic模型并采用傾向得分逆加權(quán)方法計(jì)算的總體均值估計(jì)的均值都約為0.613,非常接近,并且兩種方法估計(jì)的總體均值的方差也相差較小。在偏差與均方誤差上,傾向得分多層模型逆加權(quán)估計(jì)的偏差絕對(duì)值比傾向得分Logistic模型逆加權(quán)估計(jì)的偏差絕對(duì)值要小,而且傾向得分多層模型逆加權(quán)估計(jì)的均方誤差也較小,表明從偏差和均方誤差兩個(gè)方面來看,對(duì)于嵌套結(jié)構(gòu)的數(shù)據(jù),傾向得分多層模型逆加權(quán)估計(jì)不僅無偏程度較高,而且較有效率,估計(jì)比較穩(wěn)健。
5 結(jié)論
本文針對(duì)網(wǎng)絡(luò)候選者數(shù)據(jù)庫具有嵌套結(jié)構(gòu)數(shù)據(jù)的情況,提出建立傾向得分多層模型來估計(jì)傾向得分,并利用傾向得分逆加權(quán)方法來對(duì)非概率樣本進(jìn)行加權(quán)調(diào)整,從而推斷總體。模擬與實(shí)證研究表明,對(duì)于具有嵌套結(jié)構(gòu)的數(shù)據(jù),相對(duì)于基于傾向得分Logistic模型的逆加權(quán)估計(jì)來說,基于傾向得分多層模型的逆加權(quán)估計(jì)偏差更小,估計(jì)的效率更高。可見,傾向得分多層模型比傾向得分Logistic模型更適合具有嵌套結(jié)構(gòu)數(shù)據(jù)的網(wǎng)絡(luò)候選者數(shù)據(jù)庫。

