面板數據模型基于Within估計的最優設計

程 靖,岳榮先，王 萍

（1.安徽農業大學 理學院，合肥 230036；2.上海師范大學 數理學院，上海 200234）

0 引言

面板數據模型是一類在經濟學、心理學、管理學等科學領域中應用較為廣泛的隨機系數回歸模型[1]。由于隨機效應項的存在，很難獲得該模型中未知回歸系數的最佳線性無偏估計。常見的解決方法有兩種：一種方法是構造回歸系數的兩步估計[2]；另一種方法是設法構造回歸系數不含有未知參數的估計量[1]，其中Within估計是在計量經濟學中應用廣泛、影響深遠的一種估計量。由于消除了不可觀測的隨機個體效應，Within估計量中不再包含未知參數，并具有無偏性和一致性等優良性質，同時它也是由面板數據模型衍生的一個子模型中未知參數的最佳線性無偏估計。

在統計模型中，未知參數估計的精度會依賴于收集數據的試驗設計方案。目前有關包含多個隨機效應的隨機系數回歸模型最優設計的研究[3-6]都將隨機效應項的方差視為已知，而獲得的最優設計通常都是依賴于隨機效應項的方差比值，這在實際中較難實現。程靖和岳榮先[7]討論了單位正方形設計域上含有兩個解釋變量的面板數據基于Within估計的幾類最優恒等設計，得到了不依賴于隨機效應項方差的最優設計。由于隨機系數回歸模型中最優設計的結論并不能從單位設計域直接應用到一般設計域上，本文將嘗試對相應結論進行一般化推廣，考慮該模型在矩形設計域[a，c]×[b，d]上基于Within估計的最優恒等設計。本文首先證明了含有兩個解釋變量的面板數據模型在任意矩形設計域[a，c]×[b，d]上基于Within估計的最優恒等設計可以在 (a，b)，(a，d)，(c，b)，(c，d)四個頂點上獲得，并進一步證明了在對稱的矩形設計域四個頂點處的等權重設計是該模型基于Within估計D-、A-和I-最優設計。

1 面板數據模型的Within估計

面板數據模型可表示為：

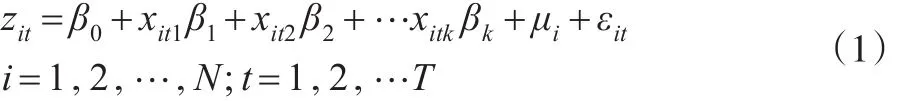
上式中zit表示第i個觀測對象在t時刻的觀測結果；xitj表示第i個觀測對象上第j個解釋變量在第t個觀測時刻的取值；β1，β2，…，βk為待估回歸系數；μi～N(0，σμ2)是第i個個體的隨機效應，εit～N(0，σ2)是隨機誤差，這里σμ2和σ2是未知參數。假定所有的隨機個體效應μi和隨機誤差εit互不相關。引入記號：

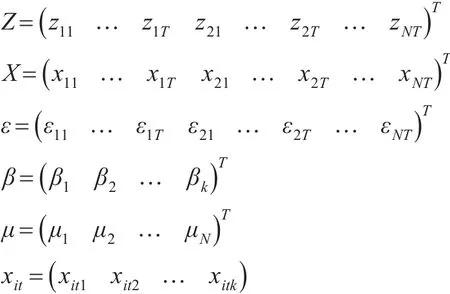
則上述模型（1）可簡化為：

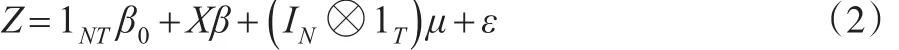
上式中1NT表示元素全部是1的NT維列向量，IN表示N階單位陣，?表示Kronecker乘積。易見：

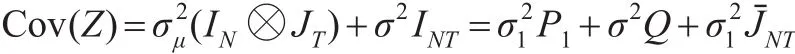
容易證明上式中的矩陣JˉNT，P，Q，P1均為對稱冪等陣，且這些矩陣是兩兩相互正交的。在面板數據模型（2）兩側同時乘對稱冪等陣Q，得到：

易得模型（3）中未知回歸系數β的BLUE（最佳線性無偏估計）是：

由式（4）所表示的估計量就稱為面板數據模型（2）中未知參數β的Within估計，并有：

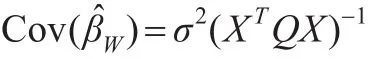
2 最優設計

本文將對程靖和岳榮先[7]中的結論進行進一步推廣，

考慮含有兩個解釋變量的面板數據模型在一般矩形設計域[a，c]×[b，d]上基于Within的最優恒等設計。為了簡便起見，下文中對含有兩個解釋變量的面板數據模型改用如下記號：

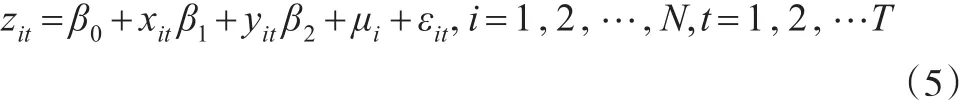
其中 (xit，yit)∈[a，c]×[b，d]。大多數實際情況下，不同單元的觀測的時刻和解釋變量的指標選取往往相同，即對 ?i，j=1，2，…，N，xit=xjt，yit=yjt。本文也僅考慮此類恒等設計中的近似最優設計。記恒等設計:

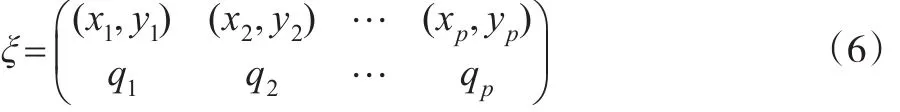
其中可以看出Within估計的協方差陣中的未知參數σ2對設計方案的選擇沒有影響，不失一般性，這里假定σ2=1。則在近似恒等設計（6）下模型（5）基于Within估計的信息陣可以表示為：

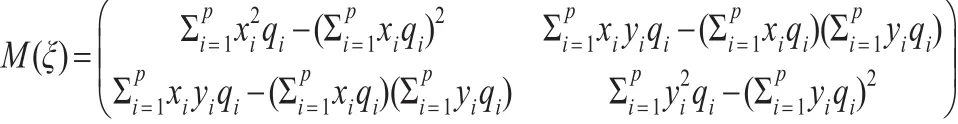
由此可以推出下述結論：

定理1：考慮含有兩個解釋變量的面板數據模型（5）基于Within估計的恒等設計，那么對設計域[a，c]×[b，d]上任一形如式（6）的近似設計，存在一個支撐點在設計域四個頂點上的近似設計：

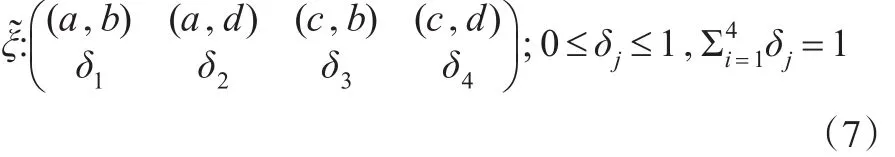
滿足M(ξ?)≥M(ξ)。

證明：令：

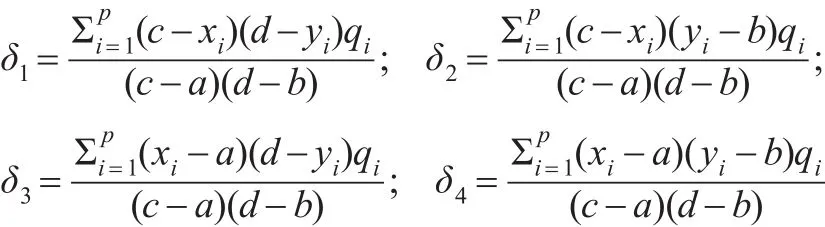
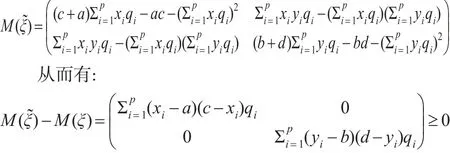
即M(ξ?)≥M(ξ)。

經典的D-、A-和I-等最優設計準則的準則函數均具有Loewner偏序性質[8]，即對兩個設計ξ1，ξ2的信息陣，如果M(ξ?)≥M(ξ)都有 Φ(M(ξ1)) ≤Φ(M(ξ2))。由于最優設計就是尋找使得信息陣的準則函數達到最小的設計，因此結合定理1的結論可知：對于由式（5）所描述的面板數據模型，其基于Within估計的最優恒等設計可在形如式（7）的設計類中獲得。在恒等設計（7）下:

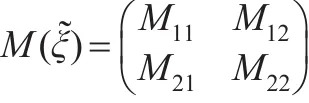
其中：

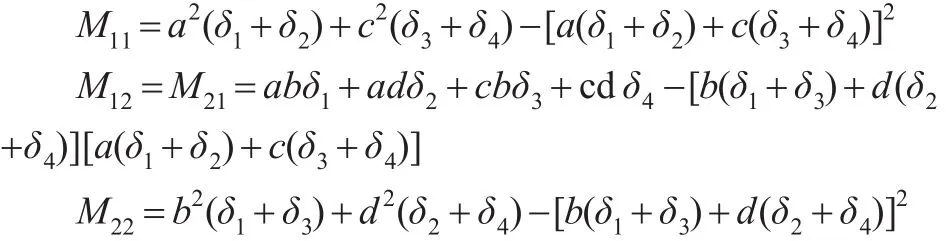
對于確定的設計域，可以通過優化上述信息陣的準則函數來獲得最優設計的解析或數值結果。本文是對其中的某一些或某一類設計域能夠獲得具有優良性質的最優設計。下面僅考慮面板數據模型（5）在對稱設計域[-h，h]×[-l，l]上基于Within估計的最優恒等設計。由定理1可知最優設計形式如下：

這里信息陣滿足：

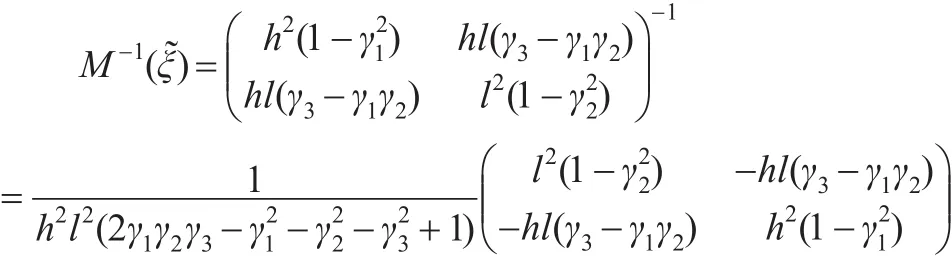
其中γ1=ω3+ω4-ω1-ω2，γ2=ω2+ω4-ω1-ω3，γ3=ω1+ω4-ω2-ω3。綜合ωj的取值范圍及設計點的個數不能少于2個可得-1＜γi＜1，i=1，2，3。

恒等設計（8）下，信息陣的D-最優設計準則函數為:

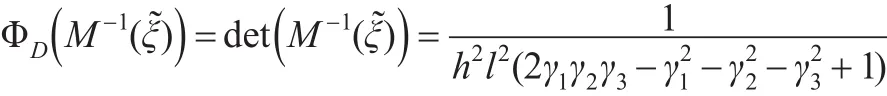
對上式分別關于γi，i=1，2，3 求偏導，并令偏導值為0，可得：

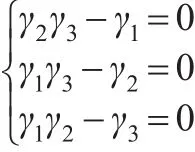
當γ2=γ3=γ1=0,即時，即ΦD(M-1(ξ?)) 取得極小值。故有定理2。

定理2：考慮含有兩個解釋變量的面板數據模型（5）基于Within估計的恒等設計，則該模型在設計域[-h，h]×[-l，l]上的D-最優設計為四個對稱頂點處的等權重設計：

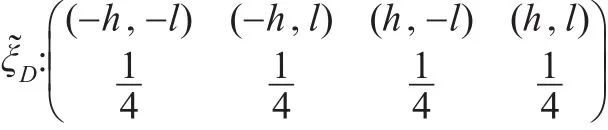
恒等設計（8）下，信息陣的A-最優設計準則函數為：

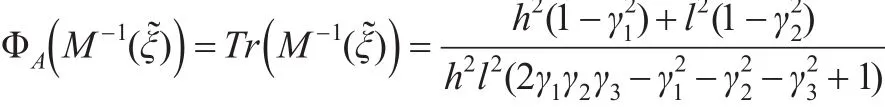
對上式分別關于γi，i=1，2，3 求偏導，令偏導值為0，可得：

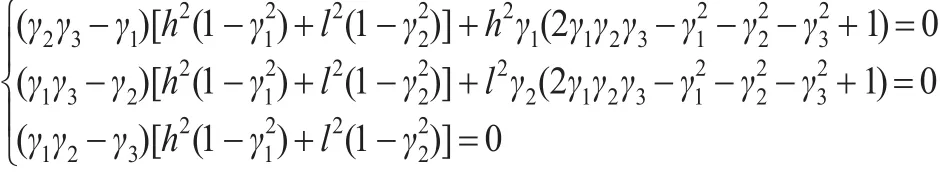
當γ2=γ3=γ1=0,即ω1=ω2=ω3=ω4=時 ，ΦA(M-1(ξ?))取得極小值。從而有定理3。

定理3：考慮含有兩個解釋變量的面板數據模型（5）基于Within估計的恒等設計，則該模型在設計域[-h，h]×[-l，l]上的A-最優設計為四個對稱頂點處的等權重設計：

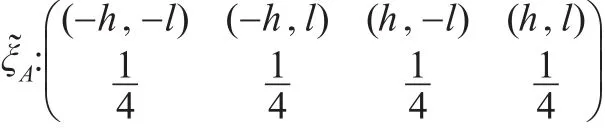
恒等設計（8）下，信息陣的I-最優設計準則函數為：

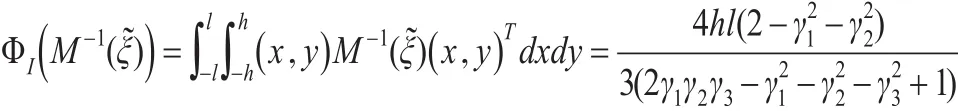
對上式分別關于γi，i=1，2，3求偏導，令偏導值為0可得：

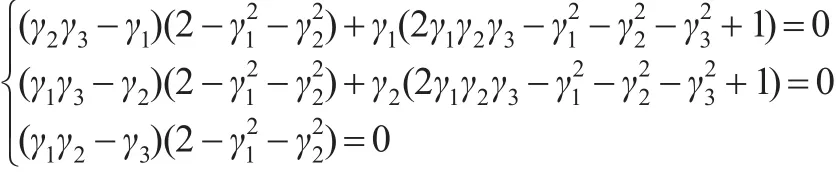
同樣可得當γ2=γ3=γ1=0 ，即時，ΦI(M-1(ξ?)) 取得極小值。故有定理4。

定理4：考慮含有兩個解釋變量的面板數據模型（5）基于Within估計的恒等設計，則該模型在設計域[-h，h]×[-l，l]上的I-最優設計為四個對稱頂點處的等權重設計：

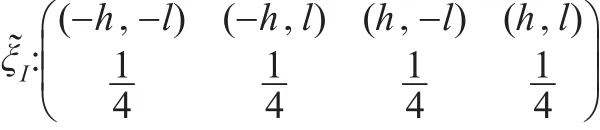
3 結論

本文對含有兩個解釋變量的面板數據模型（5）最優設計的結論進行了推廣，證明了在矩形設計域上考慮該模型基于Within估計的最優恒等設計時，仍可以將最優設計的尋找限定在設計域的頂點處。特別地，如果設計域為對稱的矩形區域，可直接采用設計域四個頂點上的等權重作為設計方案，此時等權重設計同時具有D-、A-和I-最優性質。