基于降低流固耦合振動的羅茨風機殼體結構優化*

周志海,袁澤峰

(長沙理工大學 汽車與機械工程學院，湖南 長沙 410114)

0 引言

羅茨風機為容積式風機，由于其結構緊湊、精度高、體積小、壽命長等優點被廣泛應用于建材、電力、冶煉、化工、礦山、港口、水產養殖、污水處理等各種氣體輸送領域[1]。但羅茨風機工作中產生的振動一直是影響風機穩定運行的不利因素，而引起羅茨鼓風機振動的因素較多，如地腳螺栓松動、聯軸器不合格、風機基礎剛度差、同步齒輪嚙合間隙大、轉子不平衡以及其他軸系零件松動等[2]。除此之外，由于羅茨鼓風機自身的工作特點，葉輪轉子旋轉排氣是不連續的，因此風機運轉過程中將不可避免地產生隨工作轉速變化的氣流脈動[3-4]，受此激振力作用，風機將產生不同大小的振動和噪聲。

近年來，隨著對各類機械結構動態特性要求的提高，結構動力修改問題越來越受到重視，特別是結構修改的逆問題一直是結構動力學極為活躍的研究方向[5]。風機殼體是羅茨風機的主要部件，為了提高羅茨風機運行的穩定性，改善風機在氣流脈動下的動態性能，本文針對長沙鼓風機廠有限責任公司生產的S31型羅茨鼓風機機殼，結合機殼模態分析結果及風機氣體壓力脈動分析結果對其進行結構動力修改，以減小風機殼體在氣體壓力脈動激勵下的耦合共振。

1 羅茨鼓風機機殼優化目標分析

在羅茨鼓風機機殼有限元模型各個法蘭連接處施加螺栓預緊力，并添加標準重力，利用ANSYS環境下的Block Lanczos求解方法求得機殼前6階固有頻率和振型特征(由于風機在工作情況下主要產生低頻振動，而第7階固有頻率值已接近1 000 Hz，更高階的固有頻率及振型將不具有分析價值，分析前6階模態足夠)，如表1所示。

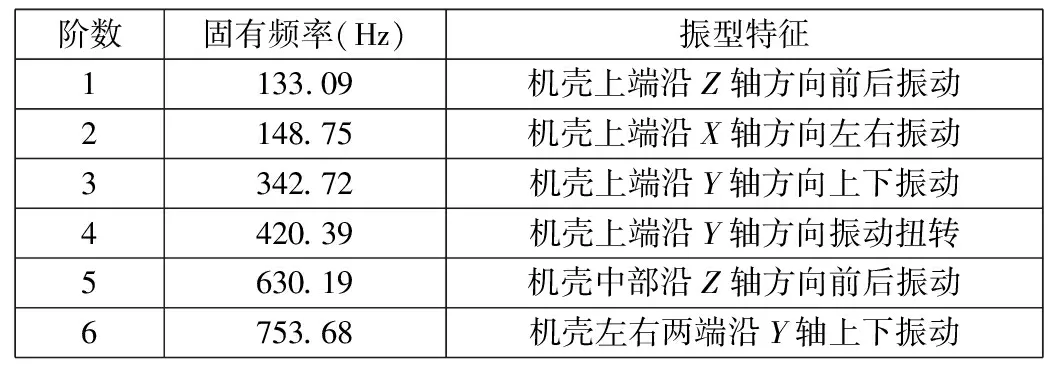
表1 機殼的前6階固有頻率和振型特征

由表1可知：①機殼前兩階固有頻率之差較小，容易發生共振效應；②羅茨風機轉速一般為490 r/min～3 000 r/min，旋轉噪聲基頻為49 Hz～300 Hz，使風機噪聲呈現低頻特征[6]。脈動激勵頻率fi的計算公式為[7]：

(1)

其中：n為葉輪轉子轉速；z為葉輪葉片數；i為基頻倍數，i=1,2,…,n。

實際工況下S31鼓風機葉輪轉子有3種穩定工作轉速：1 450 r/min、2 100 r/min、2 800 r/min。長沙鼓風機廠S31型羅茨鼓風機葉輪為一對三葉轉子，故葉輪葉片數為6。

由式(1)可計算得到各轉速下葉輪轉子產生的氣體壓力脈動激勵頻率，如表2所示。

表2 各轉速下葉輪轉子產生的氣體壓力脈動激勵頻率

表2中，1倍脈動頻率即為實際工況下葉輪轉子產生的脈動頻率，為保險起見，列出2倍脈動頻率下可能產生的脈動頻率，作為分析參考。機殼第2階、第4階振型的固有頻率分別為148.75 Hz、420.39 Hz，與表2中1 450 r/min轉速下1倍脈動頻率(145 Hz)和2 100 r/min轉速下2倍脈動頻率(420 Hz)接近，若氣體壓力脈動所產生的激勵較大，則風機在這兩種情況下運行有可能產生強烈振動和噪聲，因此需要對第2階、第4階固有頻率進行修改，以減小耦合共振。

2 結構動力修改

2.1 靈敏度分析

由于機殼殼體三維模型結構復雜、曲面較多，靈敏度分析有利于找出敏感設計點，節約設計成本，減少設計的盲目性。

結構參數對頻率的一階靈敏度可表示為[8]：

(2)

其中：ωr為結構第r階固有頻率；pm為結構設計參數或設計變量，主要指結構尺寸、幾何形狀、質量、剛度及阻尼元素等；Φr為結構第r階振型；M為結構的質量矩陣；K為結構的剛度矩陣。

若用質量元素mij代替式(2)中的pm，則可以求得質量對頻率的靈敏度表達式為：

(3)

其中：Ψir、Ψjr為結構第r階振型列向量的第i、j個元素。

為直觀分析非關鍵部位的幾何尺寸對機殼各階固有頻率的影響，改變非關鍵因素的幾何尺寸，可以改變機殼有限元模型的質量矩陣，設計變量取機殼中部兩側加強筋厚度、進出氣口端法蘭面厚度以及前后墻板法蘭面厚度(如圖1所示)，分析其對機殼的靈敏度。設計變量對機殼的前6階靈敏度分析結果如表3所示。

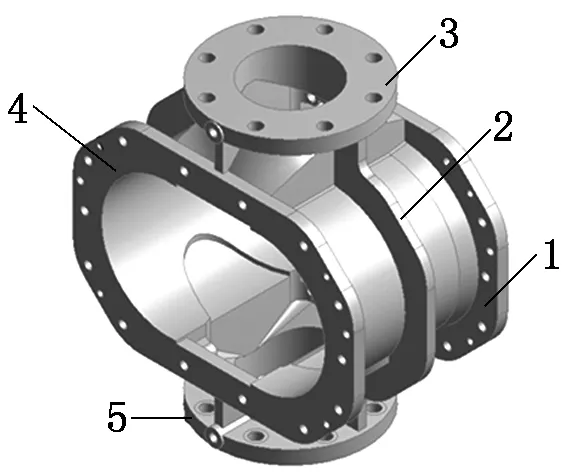
1-前墻板法蘭面；2-加強筋；3-進氣口法蘭面；4-后墻板法蘭面；5-出氣口法蘭面

表3 設計變量對機殼的前6階靈敏度分析結果 (Hz·kg-1)

由表3可知：中部兩側加強筋厚度的增大對第1階、第4階、第5階機殼固有頻率影響較小，而對第2階、第3階、第6階機殼固有頻率有較大正效應；進出氣口端法蘭面厚度的增大對第1階、第2階、第3階、第5階、第6階機殼固有頻率均有負效應，對第4階機殼固有頻率有正效應；前后墻板法蘭面厚度的增大對第2階、第5階、第6階機殼固有頻率影響較小，對第1階機殼固有頻率有較大正效應，相對其他兩個結構設計變量其對第4階機殼固有頻率有較大負效應。

2.2 機殼結構優化的設計方法

本次采取試驗設計方法(Design of Experiment，簡稱DOE)進行優化設計，具體采用的是DOE方法中較為常用的中心復合設計(Central Composite Design)[9-10]，并根據優化設計的三個基本要素確定設計變量、約束條件和優化目標，借助ANSYS Design Exporation工具完成優化。

2.3 數學模型及響應面模型分析

結合機殼固有頻率靈敏度分析結果，得到機殼結構優化數學模型：

優化目標：maxF2(X)，minF3(X).

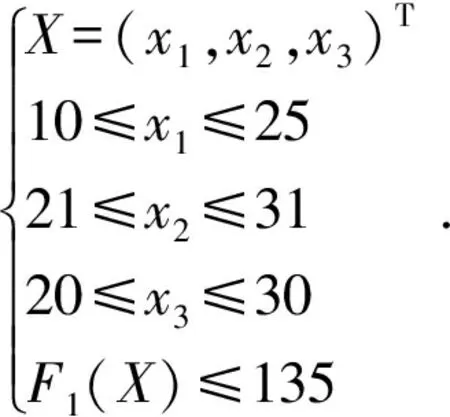
(4)

其中：x1為中部兩側加強筋厚度；x2為進出氣口端法蘭面厚度；x3為前后墻板法蘭面厚度；F1(X)為機殼第1階固有頻率；F2(X)為機殼第2階固有頻率；F3(X)為機殼第4階固有頻率。

根據式(4)所確定的約束范圍，利用中心復合設計原理，在參數的設計空間內確定了15個樣本點，得到的有限元試驗結果如表4所示。

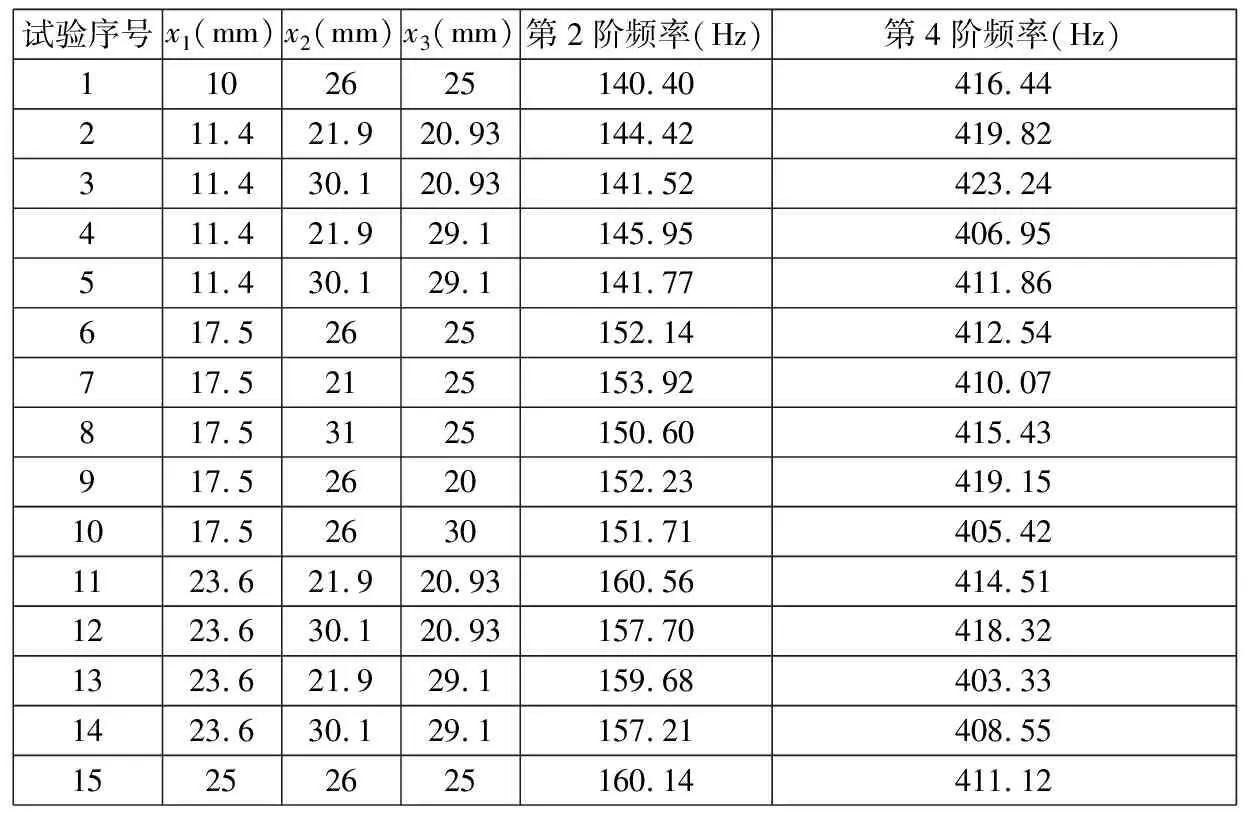
表4 基于中心復合設計的有限元試驗結果

根據表4試驗結果，以各設計變量對2階固有頻率、4階固有頻率的影響為例，利用二次插值函數構造設計空間的3D響應面，如圖2所示。

3 機殼結構優化結果分析

基于DOE試驗優化所得的有限元計算結果擬合出的響應面模型，計算得出了3組優化解，如表5所示。

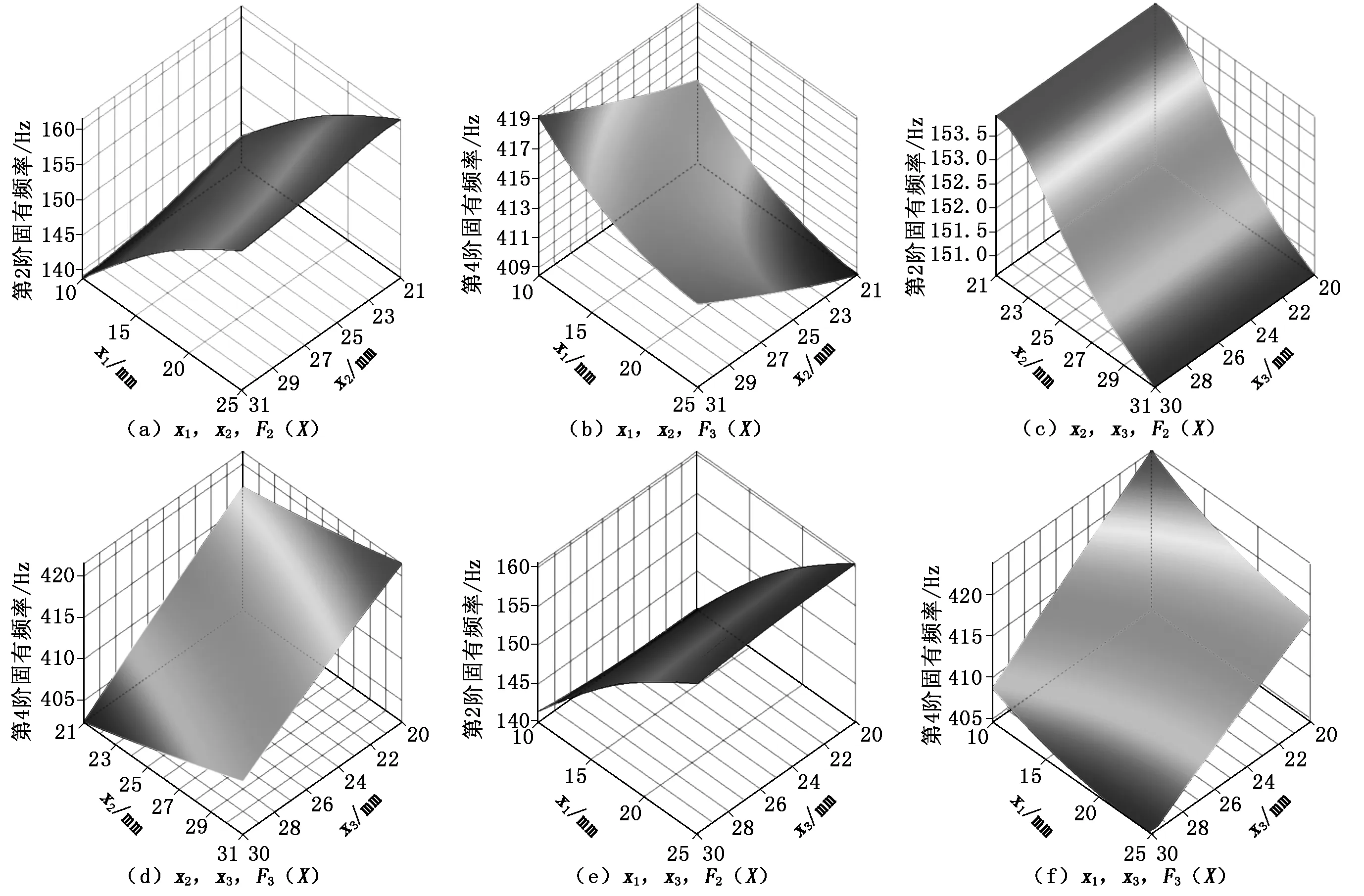
圖2 各設計變量對第2階、4階固有頻率的響應面

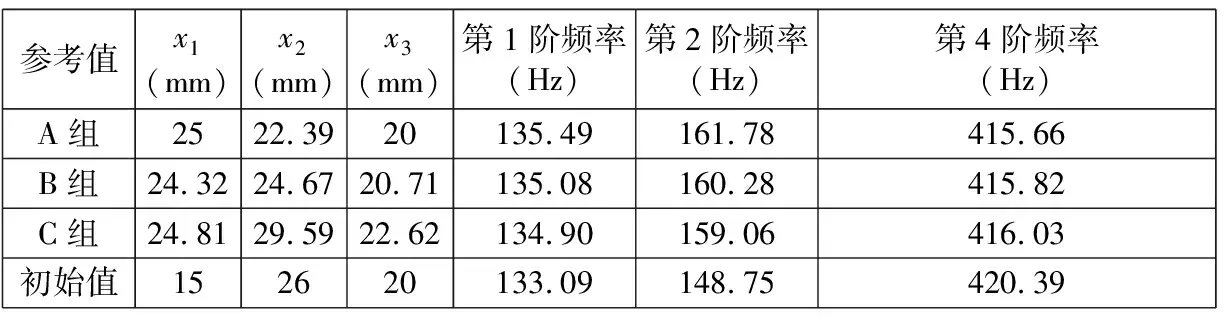
參考值x1(mm)x2(mm)x3(mm)第1階頻率(Hz)第2階頻率(Hz)第4階頻率(Hz)A組2522.3920135.49161.78415.66B組24.3224.6720.71135.08160.28415.82C組24.8129.5922.62134.90159.06416.03初始值152620133.09148.75420.39

從表5可知：A組參考值的2階頻率最優，但1階頻率相對其他兩組偏高；C組參考值1階頻率升高最小，但第2、第4階頻率結果未有A組參考值優秀；B組參考值介于A、C兩組之間。結合實際工況，在機殼結構尺寸不發生太大改變的情況下A組優化結果最為合適，修改結構后的第2階固有頻率為161.78 Hz，偏離1 450轉速下1倍脈動頻率值(145 Hz)16.78 Hz；第4階固有頻率為415.66 Hz，相比2 100轉速下2倍脈動頻率(420 Hz)偏離4.34 Hz。修改結構后可以有效地避開現有工況下的激振頻率，減小耦合共振。

4 結語

通過風機殼體模態分析結果及氣體壓力脈動分析結果發現了風機在運行中原機殼體的第2階、第4階固有頻率易與葉輪轉子產生的氣體壓力脈動頻率產生流固耦合振動。選取較為可行的結構幾何尺寸作為設計變量，利用DOE中心復合設計原理，合理布置試驗點位置，從而利用少量試驗點擬合出精度較高的響應面，再根據擬合出的響應面模型，對機殼進行參數優化設計，針對機殼第2階和第4階固有頻率進行了結構動力修改，使得改進后的機殼固有頻率分布更為合理，改進后的機殼固有頻率偏離現有工況下的氣體脈動頻率，改善了機殼的動態性能。