電動汽車直流電動機調速系統建模與控制仿真

王 鵬

(山西機電職業技術學院 汽車工程系，山西 長治 046011)

0 引言

近些年，為了保護環境，國家大力提倡使用新能源技術，純電動汽車就在這樣的大背景下快速發展起來。純電動汽車直流電動機雙閉環調速系統著重解決電動機在過載能力允許的條件下快速啟動的問題和提高系統抗干擾的問題。本文通過可視化的編程軟件Matlab建立雙閉環調速控制系統動態數學模型，并進行仿真計算，通過仿真曲線分析得出系統的不穩定因素并加以改進。

1 純電動汽車動力性計算理論基礎

本文以江淮iev6e車型為例進行分析。依據汽車理論，純電動汽車在水平路面上以最高車速行駛所消耗的功率為：

(1)

其中：η為傳動效率，η=0.92；g為重力加速度；m為汽車滿載質量，m=1 850 kg;f為路面滾動阻力系數,f=0.005;vmax為設計最高車速,vmax=60 km/h;Cd為空氣阻力系數,Cd=0.49;A為迎風面積,A=3.8 m2。

電動汽車以最大爬坡度車速爬坡時所消耗的功率為：

(2)

其中：vi為最大爬坡度車速，vi=15 km/h；i為最大爬坡度，i=0.1。

將數值代入式(1)與式(2)計算得：PV=7.55 kW，Pi=8.86 kW。選擇兩者中的較大者初步確定電動機額定功率，確定的直流驅動電動機基本參數見表1。

表1 直流驅動電動機基本參數

在額定磁通下的電動機電動勢系數為:

電動機電樞回路電磁時間常數為:

2 調速系統整流觸發裝置的數學建模與仿真分析

直流電動機驅動系統的整流觸發裝置近似于一個滯后環節，工程中近似于一階慣性環節，觸發開關頻率為15 kHz，周期T=0.066 7 ms，故觸發整流平均延遲時間Ts=0.066 7 ms。

整流環節傳遞函數為：

(3)

電流調節器傳遞函數為：

(4)

其中：Ki為電流調節器比例系數；τi為積分時間常數。

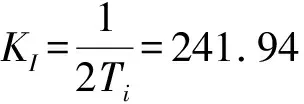
轉速調節器傳遞函數為：

(5)

其中：Kn為轉速調節比例系數；τn為轉速調節器積分時間常數。

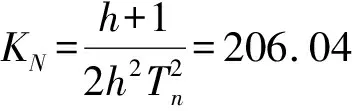
完成了理論計算工作之后，直接在仿真軟件中建立具有雙閉環調速控制系統的動態數學模型，如圖1所示。

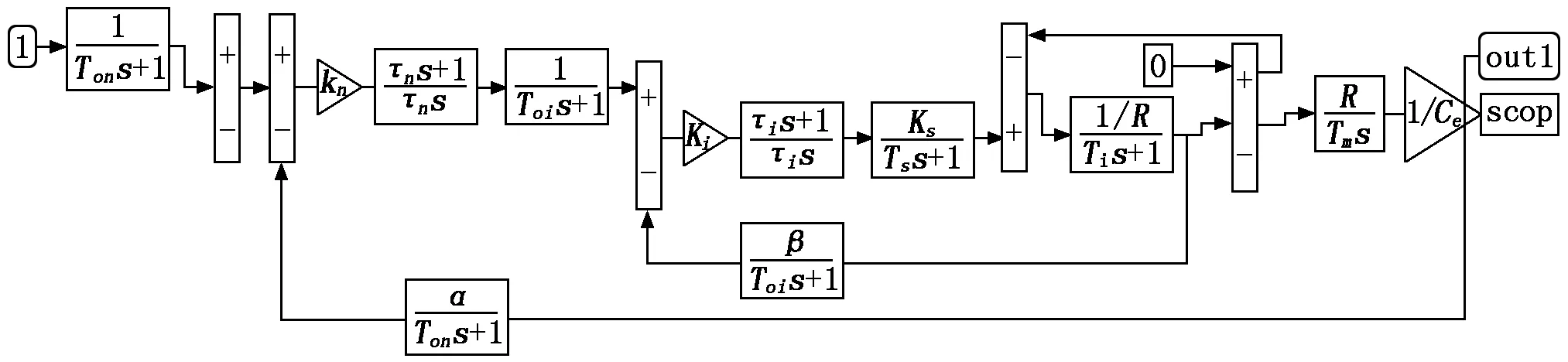
圖1 雙閉環調速系統simulink仿真模型

新建一個M文件，自動進行上述直流電動機調整系統各環節控制參數的計算，同時調用MATLAB自帶的linmod()函數直接將系統的simulink結構圖轉換為系統狀態空間模型，再調用ss()及tf()函數生成系統的傳遞函數模型。運行程序后可以得到以下結果：電動汽車需求功率為8.67 kW，系統最大超調量mp=37.072%，系統峰值時間tp=0.122 s，系統調整時間tr=0.243 s。

雙閉環調速系統的單位階躍響應曲線如圖2所示。由以上仿真結果及圖2可以得出：雙閉環調速系統的單位階躍響應品質指標總體較好，系統調整時間僅為0.122 s，可以滿足工程要求，不足的是系統最大超調量達到37.072%，不利于系統的整體穩定，應進行調整。

這里采用在原系統的最外環再加一個轉速微分負反饋環節，其傳遞函數為：

(6)

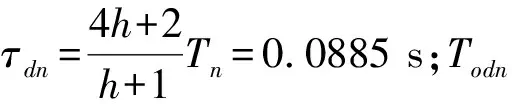
改進后的帶轉速微分負反饋雙閉環調速控制系統simulink仿真模型如圖3所示。

圖2 雙閉環調速系統的單位階躍響應曲線

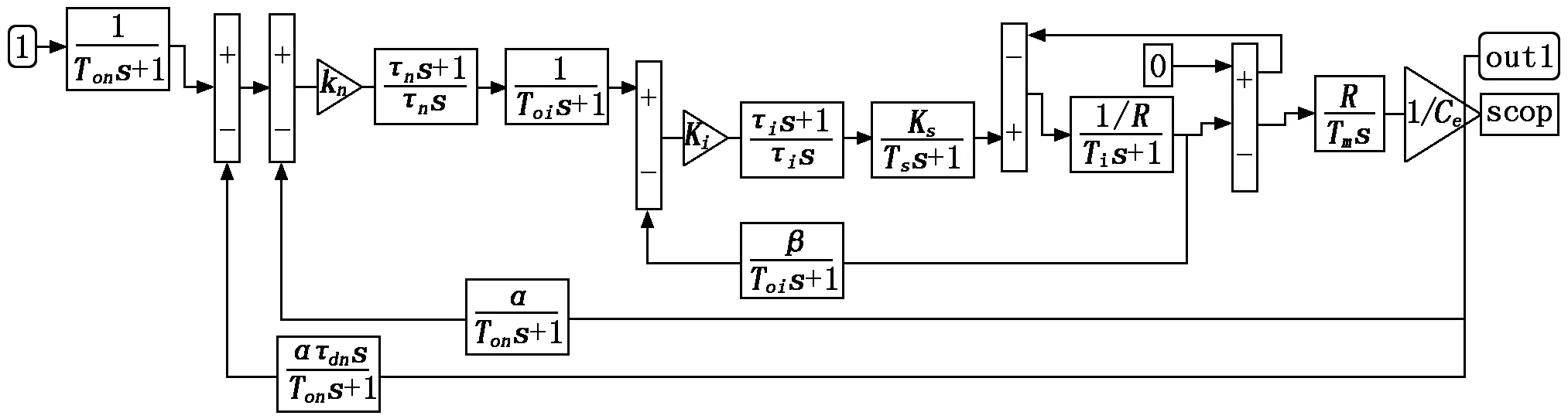
圖3 帶轉速微分負反饋雙閉環調速控制系統simulink仿真模型

再次運行程序即可以得到改進后的性能指標及帶轉速微分負反饋系統階躍響應曲線，如圖4所示。改進后的系統最大超調量mp=2.701%，系統峰值時間tP=0.431 s，系統調整時間tr=0.544 s。

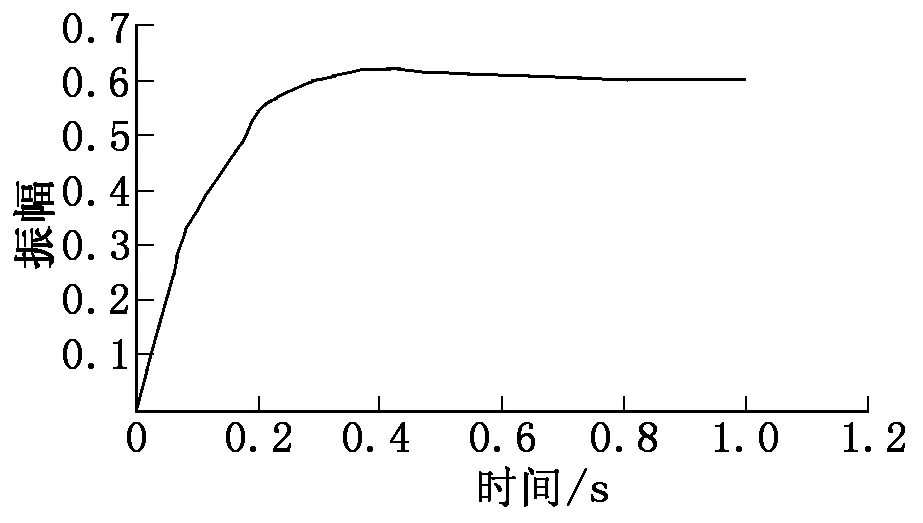
圖4 帶轉速微分負反饋雙閉環調速系統的單位階躍響應曲線

3 結論

改進后的轉速微分負反饋系統最大超調量僅為2.701%，具有優異的穩定性能，同時系統響應速度稍有滯后，但也能滿足系統需要，較好地實現了系統改進的目的。