啟用思維導圖 提高復習效率
——例析用思維導圖復習“長方體和正方體”的有效措施

浙江杭州市蕭山區錢江小學（311222）

【理論連接】

《人腦如何學數學》中指出：“如果一門數學課程主要使用嚴格規范的方法，注重記住抽象的公理和定律，那么新奇性和動機同樣會被破壞。”對于大多數人來說，要完成這些任務，需要大量的動機和興趣。

思維導圖是英國心理學家托尼·巴贊創造的一種科學有效的用腦方法。他的核心思想是按照大腦自身的規律進行思考，因此能更有效地把信息放進大腦，或者把信息從大腦中提取出來。把這一方法應用到復習課中，可以幫助學生厘清知識脈絡，攻破教學重點、難點和疑點，更好地掌握整個單元的知識和技能。

【操作措施】

回顧我任教數學的三十多年：對傳統的“雙基”念念不忘，對“四基”的實踐搖搖晃晃，特別是在我們農村小學，復習課的傳統模式是“先講后練”，四十分鐘的課堂中，10～15分鐘講解例題，其余時間讓學生自己做復習試卷。學生做得怨聲嘆氣，教師改得喘不過氣。為改變復習課的現狀，自2015年秋季開始，我用微課題的探討形式，采用思維導圖的方法上復習課，收到了較好的教學效果。

一、啟用數字思維導圖，明白重要概念

例1：大屏幕上出現一組數：

1——2——3——4——6——8——12

師：請每位同學盯著屏幕上出現的每一個數，結合今天的復習主題“長方體和正方體”，想想這些數與長方體和正方體有何聯系。

生1：長方體有六個面、八個頂點、十二條棱。

生2：每兩個相對的面的面積相等，相交于一個頂點的棱有三條。

生3：每個面有四條邊。

師：我們眼睛看著數，腦子里要聯想圖形。

例2：棱長是6cm的正方體，它的表面積與體積都是216嗎？

生1：一個是求面積，另一個是求體積，所以216cm2≠216cm3。

生2：表面積與體積的單位不同。

生3：表面積與體積的計算方法不同。

師：兩者的意義、問題、單位、計算方法都不同。

讓學生通過解讀數字導圖的含義掌握自主復習的方法，收到了較理想的教學效果。這時有一位學生深有感觸地說：“教室是與這些數字相對應的最好的場所。一個教室兩個對面相等，有長、寬、高三個維度，有四條高、六個面、八個頂點、十二條棱……”

二、采用圖形思維導圖，明確圖形特征

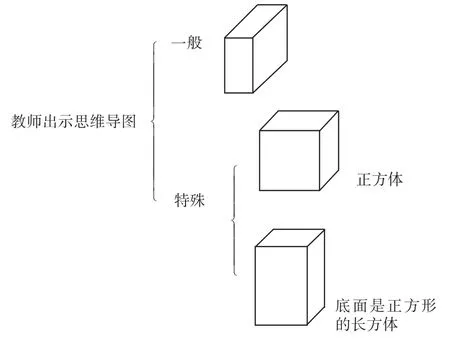
圖1

本單元有很多需要借助生活經驗來解決的數學問題，真實體現了數學知識來源于生活，服務于生活。對此，教師就要將數學課堂與學生的生活、學習聯系起來。例如，制作長方體紙箱需要的材料，教室的粉刷面積，制作玻璃魚缸需要的玻璃，游泳池貼的瓷磚，等等。教師主要是引導學生觀察、思考，先了解這些物體的特征，再根據特征計算出面積。這些知識對五年級學生來說是有難度的，現在的學生對周圍的事物關注較少，即使關注了也缺乏親身體驗。這就需要教師為學生搭建一個平臺，把實際生活中的物體做成一個模型，幫助學生慢慢建立空間觀念。

三、適用動態思維導圖，明晰內核應用

以往的復習課中，往往是教師講得越多，學生忘得越快。究其原因，是教師沒有提供具有思維含量的思考題。為改變單一作業的狀態，我在復習時，用動態思維導圖（如圖2），演示點、線、面、體的運行。

圖2

由思維導圖引導學生總結出12個字：點動成線，線動成面，面動成體；15個字：體體交于面，面面交于線，線線交于點。

在深入討論教室的“八個頂點”時，有一位平時很少發言的學生，看了圖3以后情不自禁地說：“我們家住在五樓，與住在六樓的王爺爺家相隔一層地板。我的房間和爸爸媽媽的房間也隔了一堵墻，這實際上就得到了兩個長方體。”

圖3

在如此教學后，學生完成以下五道練習題的平均正確率達到85%。

題1 請你舉出日常生活中長方體物品的例子，最少舉6個。

題2 將一塊長12厘米、寬3厘米、高5厘米的長方體木塊平均分成三塊后，木塊的表面積增加了多少平方厘米?

題3 小明用圖4中的6塊玻璃（單位：厘米）拼成一個金魚缸養金魚。請問有幾種做法?（寫出所選的玻璃號碼，畫出金魚缸的立體圖形）

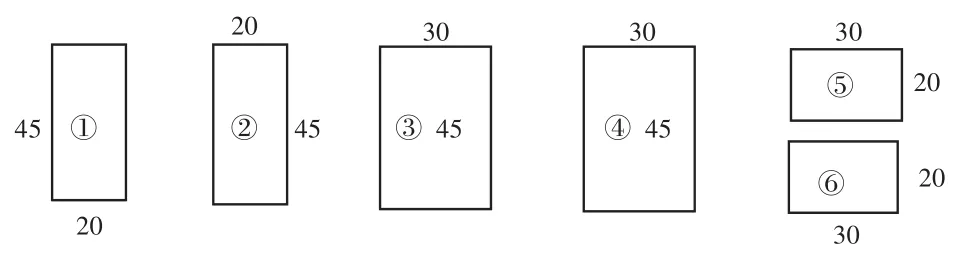
圖4

題4 填空。

（1）用一根24厘米長的鐵絲焊成一個最大的立方體模型，它的表面積是（ ）平方厘米，體積是（ ）立方厘米。（2）一個底面是正方形的長方體，底面周長是20厘米，高是12厘米，它的表面積是（ ）平方厘米，體積是（ ）立方厘米。

題5 圖5-1是由36個小積木堆成的。把圖5-1推倒后變成圖5-2，再利用這堆小積木在圖5-3上四個四個地往上堆成一幢“大樓”。這幢“大樓”有幾層?

圖5-1

圖5-2

圖5-3

四、妙用展開式思維導圖，明了拓展價值

先由一個問題開始，再引入思維導圖。

問題：切一刀后增加幾個面呢？

圖6

師：這個大立方體（如圖6）一共被切了幾刀？有幾個小立方體？它的表面積增加了多少？要弄清這個問題請先看思維導圖（圖7）。

圖7

師：我們實驗室的長是9.5米，寬是5.4米，高是4.5米，高老師和41位同學一起在實驗室里做實驗，能算出平均每人能呼吸到多少立方米的空氣嗎？

無盡的駕駛樂趣，令人瘋狂的激情，令人沉醉的體驗，“從天而降”的六輛跑車為我們略顯枯燥的生活帶來不一樣的精彩。

生1：這怎么算呀？

生2：不是很簡單嗎？只要算出9.5×5.4×4.5÷41的結果就可以了。

生3：不行，應該除以42。因為高老師應該也要算進去。

生4：不對，計算總體積時并沒有把我們42個人的體積算進去。

生5：我們人體的體積怎么算呢？

生6：可以算。可以用阿基米德的方法算出每個人的體積。

生7：那教室里的課桌椅也占了體積。我估計課桌椅的體積可能是5立方米，所以我認為總體積應該是教室的體積減去26立方米。

（最后大家一致同意生7的看法，經過計算知道每個人能呼吸到的空氣約等于4.88立方米）

這個學習的過程給了學生一次實際而真切的感受：對具體問題要具體分析。一位平時思維不是很活躍的學生對我說：“我在解題時一看到數據就很興奮，所以把高老師給忽略掉了，對不起，以后我一定在審題時認真仔細，不斷提高解題的正確率。”

這樣的解題教學符合杜威在《我們怎樣思維·經驗與教學》中指出的“學習就是要學會思維”。蘇霍姆林斯基認為：“學校生活的全部意義主要在于培養學生的獨立思考能力。”因此，從小學開始，如何把學生培養成“思想家”“思考者”“高階思維王子”，主動地讓學生認真思考、積極猜想，“讓兒童找到數學思維的樂趣”是教師一直需要思考的。

本單元的特點是計算比較多，但是在學習完長方體和正方體的體積計算之后，很多學生不能夠認真分析題意，拿到題目就直接計算長方體或者正方體的體積。這樣就容易出現錯誤，尤其容易是把計算表面積的題目當成了求體積。表面積的計算涉及較多的實際問題，例如在計算粉刷教室需要多少涂料時，很多學生不考慮具體的情況，直接就套用表面積計算公式。對此，教學時我主要是讓學生觀察教室是怎么樣的，數一數需要粉刷的一共幾個面，不用粉刷的是哪個面，還應該去掉哪部分……對于在學習完體積之后，不知道是計算表面積還是體積的學生，我主要引導他們從問題入手，例如可以看題目中問題的單位，根據單位來確定要求什么。

在教學的過程中，我了解到了每一位學生的認知心理和認知邏輯起點，所以設計了以下應用題：

題6 圖8是由棱長為2厘米的小正方體壘成的實心的一個零件,這個零件的體積是（ ）。

題7 如圖9，把長方體的6個面分別展開，請按照你觀察的方位，填寫“前、后、上、下、左、右”。

圖9

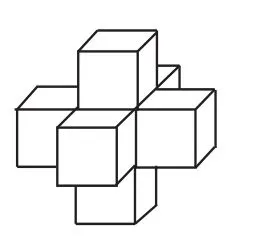
圖8

【實踐感悟】

1.清清楚楚幾個數，搞懂名稱不費勁

啟用數學思維導圖后，大多數學生立馬能明確數字與圖形之間的緊密聯系，為學生從平面圖形向空間觀念的發展奠定了基礎。

2.明明白白三個圖，各自特征不死記

學生往往搞不清楚從屬關系與并列關系，用了思維導圖以后，學生就能夠明確一般的長方體，知道底面是正方形的長方體和立方體是有異同的。

3.仔仔細細算題目，實際應用不出錯

學生對切一刀產生兩個面這個模型認識不清，但用了思維導圖以后，他們在計算當中都很少犯錯。

4.認認真真拓思路，疊加分拆不害怕

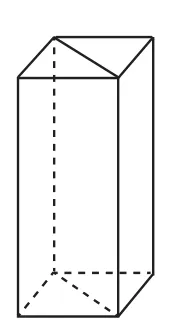
圖10

拓展思維是學生學習立體幾何的一種重要的思維方式。有一個學生在利用思維導圖復習了長方形和正方形的體積相關知識后，就能夠很快指出：“圖10中，如果長方體的長是4，寬是3，那么對角線一定是5。我還能算出這一刀切下去得到的長方形的面積，而且明白了切一刀多兩個面的道理。”

總之，使用思維導圖開展復習課是符合學生學習實際和生活實際的，它能培養學生集中與發散的思維，且能從學生的興趣出發，培養樂趣，產生情趣，發展志趣。可以說，思維導圖是引發學生積極思維的發動機。