中美初中數學教科書有理數例題的比較研究

王曉麗，張明亮

?

中美初中數學教科書有理數例題的比較研究

王曉麗，張明亮

（河南大學 數學與統計學院，河南 開封 475004）

選取人民教育出版社七年級上冊數學教科書與美國McGraw-Hill出版社的教科書中有理數的例題作為研究對象，從例題數量、側重的內容、表示形式、背景素材、文字特征、特色模塊等方面進行比較分析．對人教版初中數學教科書有理數章節例題的編寫提供如下建議：增加利于理解有理數概念的例題數量，避免重運算輕概念；改變教科書對循環小數“零涉及”的狀態；根據認知難度分配有理數各形式例題的比重；豐富例題背景素材；創設有代表性的特色模塊．以期通過對比研究對合理配備有理數例題提供參考．

數學教科書；例題；比較；有理數

1 問題提出

教科書作為教學的主要載體，一定程度上影響著教育的發展走向．在數學教科書的編寫上，一個重要的環節就是建立配套的例習題體系[1]，而例題是教科書中概念定理與習題之間的橋梁和紐帶．教科書例題具有示范引領、鞏固新知、展示新知、思維訓練、揭示方法、文化育人等功能[2]，學生獲得數學概念、掌握數學定理、發展數學能力都離不開例題[3]．因此，對教科書例題的研究十分必要且有意義．

顧泠沅教授指出，從學生接觸正式數學與應用數學的機會上看，PISA測試中成績高的幾個東南亞國家大多處于高正式，低應用象限[4]，而美國等西方國家的學生則大多具有較高的創造力和應用能力．蔡金法教授曾用簡單的計算題、問題解決題、過程限制的復雜題、過程開放的復雜題4種不同的題目去測試中國和美國六年級的學生．研究結果表明，中國學生在前3種題目的測試中，成績遠高于美國學生，而美國學生在開放題中的測試成績卻高于中國學生，這樣的樣本所代表的差別一定程度上可以反映兩國整個群體之間在數學教育上的差別[5]．

他山之石，可以攻玉．比較是為了知己知彼，學他人之長處，改自身之不足[6]．美國學生具有的良好創造能力正是中國教育期望中國學生提升的能力．因此以美國教科書（以下簡稱CM教科書）與中國人民教育出版社七年級上冊數學教科書（以下簡稱RJ版教科書）作為比較研究的對象，發現美國教育對學生實際應用水平和創造能力的培養在其教科書中的體現．

由于從小學到中學，學生從學習自然數到整數、分數再到有理數，接觸的數越來越具有抽象性．作為學生剛步入中學便接觸到的內容，大多數學生對有理數的掌握情況并不理想，而有理數是數與代數部分的基礎內容，是日后學習無理數和實數的根基．所以，如何更好地配備有理數部分的例題，使學生真正理解并掌握有理數顯得尤為重要．

RJ版教科書在有理數章節未涉及循環小數的內容，對有理數定義的解讀不完全．而CM教科書對有理數的定義嚴謹而準確，并配有例題進一步解釋說明為何循環小數是有理數．兩版教科書的例題在側重內容、有理數表現形式以及背景素材等方面差異顯著．

因此，通過對兩版教科書有理數例題的比較研究，豐富提升中國RJ版教科書有理數例題的內容和質量，同時也通過對比來探討兩國學生間的差異在教科書中的體現，引導中國吸收借鑒美國教育的特色，促進中國數學教育更好地進步．

2 研究對象

2.1 教科書的選取

兩國教科書具體信息如表1所示．

表1 教科書信息

2.2 研究內容的選取

RJ版教科書有理數章節的例題用“例”或者“例1”“例2”標出，沒有具體的模塊劃分；CM教科書有理數章節的例題分為“例題（examples）”“現實世界舉例（real-world example）”兩個模塊．

這里選取RJ版教科書第一章“有理數”的全部例題以及CM教科書第二章“有理數”的全部例題進行比較研究．

3 研究工具及方法

3.1 研究工具

選擇鮑建生教授建立的綜合難度模型為研究工具之一，結合有理數例題的特點對其進行選擇和調整，將鮑教授對背景因素的水平劃分改為無背景、學科相關聯背景、日常生活背景和無實際意義背景4類進行比較研究．

該研究結合有理數例題的特點對戴再平教授建立的例題分類稍加調整后作為研究工具，根據各類型例題所占比重進行分析；選取黎野平教授構建的分析問題3層面為研究工具，對有理數例題的文字特征進行對比分析．

3.2 研究方法

以定量刻畫與定性描述相結合的方法，通過文獻研究、內容分析和教材比較，對兩版教科書有理數的例題從數量、類型、形式、背景、文字特征等方面進行細致探究．

4 研究過程與結果分析

4.1 例題數量比較

RJ版教科書有理數章節共有42道例題，CM教科書有理數章節共有59道例題．整體而言，CM教科書有理數例題數量多于RJ版教科書，具體見圖1．

圖1 兩版教科書有理數例題數量比較

4.2 例題類型比較

戴再平教授將例題分為概念型、原理型、方法型和問題解決型[7]．根據有理數例題的特點并結合戴再平教授對例題的分類將有理數章節的例題劃分為概念型、原理（法則）型和問題解決型3類，根據這3種分類對兩版教科書有理數的例題進行分析歸納，繪制如圖2所示折線圖．

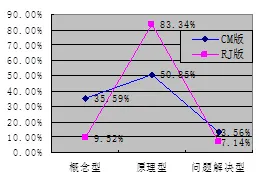
圖2 兩版教科書有理數例題類型比較

RJ版教科書有理數章節的例題集中出現在有理數加減法和乘除法運算等小節中，在1.2.1有理數概念的小節中未涉及任何例題，這一定程度上反映出RJ版教科書有理數章節更注重對運用法則進行運算的例題的掌握，而相對忽視對有理數概念的理解，這個結論也在圖2中得到了體現．

RJ版教科書給出的有理數的定義是“整數與分數統稱為有理數”[8]（如圖3）．在數的列舉中，只在旁邊標注說明“這里列舉的小數可以化為分數”（如圖4），從而直接將小數劃到分數之中，并沒有舉出例題解釋為何小數和分數可以進行互化．

圖3 RJ版教科書有理數定義

圖4 RJ版教科書旁白解釋

另外，循環小數作為有理數卻沒有在圖3的舉例中被列舉出來，全章節的內容中也未涉及任何循環小數的知識，這種對概念的不完全解讀，會阻礙學生對有理數的透徹理解和認識．

CM教科書有理數章節屬于概念型的例題比RJ版教科書高26.07個百分點，概念型和原理（法則）型例題相對而言較平衡．CM教科書每小節的內容中都有例題，一般設立在KEY CONCEPT模塊之后來幫助學生理解概念．CM教科書對有理數的定義是“那些可以被表示成分數的數稱為有理數”[9]，并指出有限小數和循環小數都是有理數，因為它們可以表示成分數．在給出定義后，設置例題對為何有限小數和循環小數可以表示成分數給出具體的講解（如圖5）．

同樣，CM教科書也對分數化有限小數和循環小數設置例題進行講解，使學生學會互化，真正弄懂有理數的概念．

通過比較，兩版教科書有理數例題中問題解決型的例題比重差異不大，但是概念型例題所占比重差異顯著．CM教科書對有理數概念的分析透徹清晰，比RJ版教科書更注重幫助學生理解有理數的概念．張奠宙教授曾說過：“西方在數學教學中強調理解、理解、再理解，而中國則是練習、練習、再練習．”[10]李士锜教授也在其著作中提出西方教育與中國教育在理解與練習方面的思想差異[11]．這些都在一定程度上體現出美國教育比中國教育更加注重學生理解為什么，而不是僅僅知道怎樣做．

4.3 有理數各形式所占比重比較

有理數一般通過整數、分數、有限小數、無限循環小數4種形式來考查．以下對兩版教科書有理數例題中這4種形式例題的數量進行比較分析．

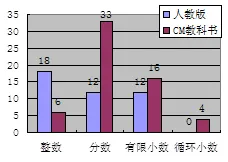
圖6 兩版教科書有理數各形式所占比重比較

從認知難度上看，循環小數、有限小數和分數形式的數的理解要比整數困難，但是RJ版教科書中以整數形式考查有理數的例題數目要多于分數和小數，對形式不易理解的數的舉例少于易理解的數，甚至未涉及循環小數的例題，這易導致學生對難點掌握不牢固．CM教科書中以分數、有限小數形式考查有理數的例題數量要大于整數，相比RJ版教科書更遵循學生的認知難度．

上述數據表明CM教科書有理數例題的配備更加有助于學生理解難點，攻克難點．

4.4 例題背景素材比較

鮑建生教授建立的背景因素的水平劃分，將數學題分為無實際背景、個人生活背景、公共常識背景、科學情境背景[12]4類．結合有理數例題的特點，將鮑教授的劃分改為無背景、學科相關聯背景、日常生活背景和無實際意義背景4類．根據這4種分類對兩版教科書有理數例題的背景素材進行比較分析，繪制如圖7所示的折線統計圖．

圖7 兩版教科書有理數例題背景素材比較

整體來看，RJ版教科書與CM教科書有理數章節的例題素材選取具有一定的共性，即均是無背景的例題所占比重大，且無背景的例題均是有理數加減乘除運算等類的題目．另外，兩版教科書有背景的例題中，均有一小部分例題只是為了有背景”而創設背景，例題的背景素材無實際意義．

但是相比較而言，CM教科書例題中有意義的背景素材更加豐富，比RJ版教科書高11.5個百分點．

CM教科書有理數內容中涉及學科相關聯背景素材的例題有5.08%，而RJ版教科書例題中未涉及與其它學科相關的背景素材，表明CM教科書更加注重引入與其它學科相關聯的背景知識，如數學在物理、化學和生物乃至體育等學科的應用，促使學生意識到數學的廣泛用途．

RJ版教科書和CM教科書有理數內容中涉及“日常生活”的例題分別占例題總量的7.14%和13.56%，CM教科書超過RJ版教科書6.42個百分點，表明CM教科書更加注重對與學生日常生活相關的背景素材的引入．

上述結論體現出美國教科書更注重培養學生對數學的興趣以及對數學廣泛用途的認識，利于學生的直接興趣和間接興趣的培養．這與不少學者經研究得到的美國教育更關注學生興趣，注重數學與實際生活的聯系的觀點不謀而合[13-14]．另外，美國著名的“教師年度人物”評選活動的首要標準是“如何讓學生的學習興趣更濃厚”，這也促進了美國教師對學生興趣培養的重視[15]．

4.5 例題文字特征比較

李業平建構的分析問題的3個層面分別是，數學特征、文字特征和達到要求．從文字特征層面將數學例題分為“只有數字和文字的形式（PM）”以及“有圖表解釋或故事背景（IC）”兩類[16]．根據這兩種分類對兩版教科書有理數例題的文字特征進行對比分析，繪制如圖8所示的柱狀圖．

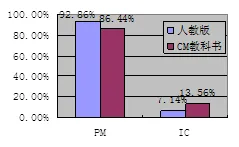
圖8 兩版教科書有理數例題文字特征比較

由圖8數據可知，兩版教科書有理數例題的文字特征均是以“只有數字和文字形式”的例題為主．

但是相比較而言，RJ版教科書有理數例題中只有數字和文字的例題所占比重更大，CM教科書有理數例題中有圖表解釋或故事背景的例題所占比重高于RJ版教科書6.42個百分點．表明CM教科書有理數例題中的圖表和故事背景相對豐富．

另外，與RJ版教科書有理數例題中的卡通插圖相比，CM教科書有理數例題中的插圖均為實景圖，相對而言更加貼近生活．

4.6 例題特色模塊比較

RJ版教科書的例題模塊相對單一，以“例”“例1”“例2”來劃分，例題一般按照從易到難，從基礎到應用的順序排列．

CM教科書的例題一般分為“例題（examples）”“現實世界舉例（real-world example）”兩個模塊．有理數章節“例題”模塊下的題目是概念理解或運用法則的計算類基礎題．“現實世界舉例”模塊下的例題均是與實際生活相關的應用題，該模塊的特別之處在于每個例題旁邊都會附有實景插圖和相關背景的介紹來豐富學生的認知（如圖9）．

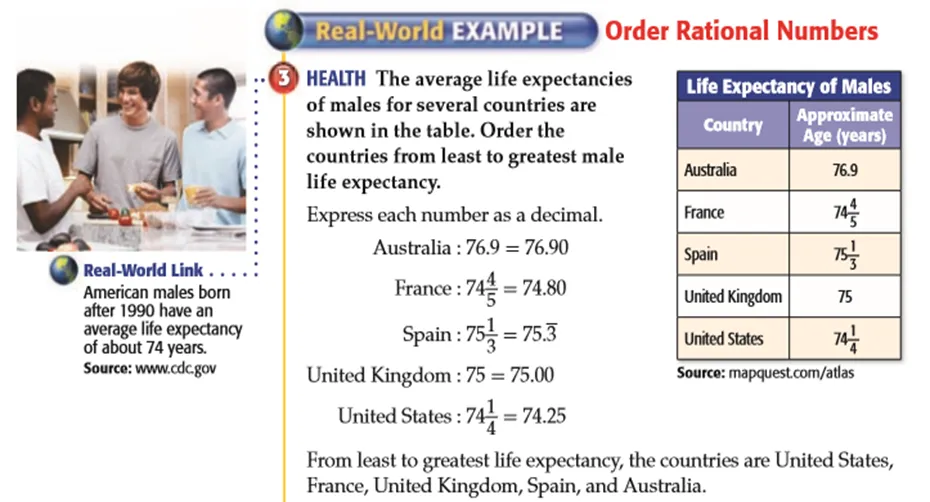
圖9 CM教科書特色模塊示例

5 思考與建議

比較是為了取他人之長改自身之不足，選取美國教科書進行比較研究，是期望取其精華之處，推動中國教科書的改革進步．但這并不代表要盲目效仿美國教科書，美國學者所寫的中美數學教科書比較的論文中也在尋找其自身的不足，虛心向中國教科書學習．如美國學者Lo Jane-Jane指出中國教科書“比率和比例”（ratio and proportion）[17]部分的例習題，較復雜的題目要多于美國教科書，并提倡向中國學習．對此，中國數學教科書的編寫應找到基礎與創新、理論與實際生活的平衡點，保持中國學生“基礎扎實”的長處的同時努力提升不足之處．

（1）意識到概念是運算的基礎，找到概念題和計算題的平衡點．

例題貴在精而不是貴在多，數學是需要思考的，數學教育的目的也不是培養熟練的工種[18]，因此有理數例題的配備除了注重學生運算能力，也要注重學生對有理數概念的理解與掌握，不能只注重是什么，更要知道為什么．RJ版教科書有理數的例題全部出現在有理數加減乘除運算的小節中，在1.2.1有理數小節中沒有出現例題，這一定程度上體現出RJ版教科書重運算而輕概念．相反，CM教科書在每小節的KEY CONCEPT（核心概念）模塊后都列舉一或兩道例題來幫助學生理解所給概念．

先有數后有運算，數的概念是運算的基礎．RJ版教科書要避免重運算輕概念，在給出有理數的定義后，應該適當舉例來幫助學生透徹地理解有理數的概念．在這一點上，可以學習CM教科書，首先表明并非所有小數都可以化為分數，僅有限小數和循環小數可以化為分數，然后舉出分數化有限小數、有限小數化分數以及分數化循環小數、循環小數化分數的例題，使學生通過實際的動手計算，真正地明白為何有限小數和循環小數都可以看作分數，從而真正地理解有理數概念．

（2）注重教科書的嚴謹性，彌補對循環小數舉例的缺失．

RJ版教科書不僅在對有理數進行歸納時略去了循環小數的舉例（如圖3），在有理數整章的課程內容及例題和練習題中也都未出現循環小數．教科書具有權威性和強大的影響力，這種舉例的匱乏可以視為對概念的不完全解讀，會導致學生對有理數的概念認知不清．RJ版教科書可以參考CM教科書對有理數概念的引入來彌補對循環小數舉例的缺失（如圖10）．另外，RJ版教科書也要改變對循環小數“零涉及”的狀態，適當增添循環小數形式的例題以及練習題．

圖10 CM教科書有理數核心概念

（3）根據學生對有理數各表示形式的認知難度分配各形式例題的比重．

從認知難度上看，分數和小數形式的數的理解要遠比整數困難．因此，RJ版教科書有理數章節的例題可以根據知識理解的難易程度來適當調整各形式例題的比重，改變目前以整數為主的例題形式，適當增加分數和小數形式考查有理數的例題比重，幫助學生更好地理解難點．

（4）增添有意義的例題背景素材，使學生意識到數學與生活及各學科之間的緊密聯系，吸引學生的直接和間接興趣．

RJ版教科書與CM教科書中分別有4.76%和3.39%的例題背景是無實際意義的，如CM教科書中的一道例題（如圖11所示）．

圖11 CM教科書例題示例

“鉆頭”應該無法吸引初中一年級學生的興趣并且與他們的日常生活有一定的距離．

引入素材的目的是為了借助與實際生活相關的背景知識把抽象的數學生活化，或者通過與其它學科相關的背景知識使學生認識到數學的廣泛用途，而無實際意義的素材的引入只是增添了學生的閱讀負擔．因此，RJ版教科書要注意提升例題背景素材的質量，選取恰當的題材來吸引學生．

4.4中的數據及分析表明，CM教科書有理數例題的背景素材比RJ版教科書豐富．RJ版教科書可以參考CM教科書在每小節設立“現實世界舉例”模塊的方法（如圖12），設立相關模塊列舉與學生日常生活相關聯的例題吸引學生的直接興趣，或通過列舉與其它學科相關的例題使學生認識到學好數學知識的重要性，從而激發其求知欲，培養學生的間接興趣．通過對有理數例題的背景素材的豐富，使學生體會到數學的生活價值和文化價值[19]．

（5）豐富例題的呈現形式，創設教科書的特色模塊．

RJ版教科書應適當改變以單一文字或數字形式為主的例題呈現方式，增添有圖表解釋或故事背景的例題，創設具有自身特色和代表性的多樣化的例題模塊，使RJ版教科書的數學知識更加生動形象，得到學生的喜愛．

圖12 CM教科書例題示例

[1] 吳立寶．中澳數學教科書習題比較研究——以人教版和HMZ8年級教科書為例[J]．數學教育學報，2013，22（2）：59-61．

[2] 吳立寶，王富英，秦華．數學教科書例題功能的分析[J]．數學通報，2013，52（3）：18-20．

[3] 張文宇，張守波．海峽兩岸小學數學教材分數內容例題的比較研究[J]．數學教育學報，2015，24（3）：68-71．

[4] 顧泠沅．中國學生為什么數學那么好[N]．中國教育報，2013-12-04（3）．

[5] 蔡金法．改進中國數學教育的六點思考——基于中美學生數學學習的系列實證性研究（上）[J]．小學青年教師，2016（10）：24-25．

[6] 高文君，鮑建生．中美教科書習題的數學認知水平比較——以二次方程及函數為例[J]．數學教育學報，2009，18（4）：57-60．

[7] 戴再平．數學習題理論[M]．上海：上海教育出版社，1991：89．

[8] 人民教育出版社課程教科書研究所，中學數學課程教科書研究開發中心．義務教育教科書（數學）七年級（上冊）[M]．北京：人民教育出版社，2013：2-52．

[9] DAY, FREY, HOWARD, et al. Glencoe California mathematics 7 [M]. California: The McGraw-Hill Companies, 2008: 84-141.

[10] 鄺孔秀．“理解是第一位”嗎[J]．數學教育學報，2000，9（3）：95-99．

[11] 李士锜．數學教育心理學[M]．上海：華東師范大學出版社，2001：64-87．

[12] 鮑建生．中英兩國初中數學期望課程綜合難度的比較[J]．全球教育展望，2000，29（9）：48-52．

[13] 史炳星．從課程內容看美國教育的觀念和方法[J]．數學通報，1999，38（10）：35-37．

[14] 張偉平．TIMSS測試的認知診斷評價標準下中美學生數學能力比較[J]．數學教育學報，2010，19（4）：66-69．

[15] 吳仲和．比較研究要重視教育政策和背景——從不同角度看美國數學教育[J]．數學教育學報，2017，26（4）：35-36．

[16] ?LI Y P. A comparison of problems that follow selected content presentations in American and Chinese mathematics textbooks [J]. Journal for Research in Mathematics Education, 2000, 31 (2): 234-241.

[17] ?LO J J, CAI J F. A comparative study of the selected textbooks from China, Japan, ChineseTaiwan and the United States on the teaching of ratio and proportion concepts [J]. ERIC Publications, 2001, 18 (21): 509-520.

[18] 曹一鳴，辛興云．從數學本質解讀數學課程改革[J]．數學教育學報，2005，14（1）：42-45．

[19] 葉立軍，王曉楠．中美高中數學教材比較研究——以“幾何概型”為例[J]．數學教育學報，2012，21（2）：50-52．

Comparative Study on Rational Numbers Examples in Mathematics Textbooks for Junior Middle School in China and the United States

WANG Xiao-li, ZHANG Ming-liang

(School of Mathematics and Statistics, Henan University, Henan Kaifeng 475004, China)

The examples of rational numbers were chosen as the study objective in mathematics textbooks by People’s Education Press in China and the California Mathematics by McGraw-Hill in the United States. A number of aspects in these examples were compared and analyzed, including the quantity, the emphasis, the types, the material of the background, the text feature and the typical modules. This study provided some suggestions for writing mathematics textbooks examples in junior high school in our country, including adding the number of concept examples, adding some examples of repeating decimals properly, allocation examples according to the difficulty of cognitive, enriching the background of examples, and creating the typical modules. Through this comparative study, we hoped to provide a reference for more appropriate compilation of examples in rational numbers.

mathematics textbooks; examples; comparison; rational numbers

G633.6

A

1004–9894（2018）06–0067–05

王曉麗，張明亮．中美初中數學教科書有理數例題的比較研究[J]．數學教育學報，2018，27（6）：67-71．

2018–06–28

王曉麗（1993—），女，河南鄭州人，碩士研究生，主要從事數學教育和教科書比較研究．

[責任編校：周學智、張楠]