連貫性視閾下“代數思維”課程設置的比較研究——以“中”“美”“英”“澳”“新”“南非”六國課程內容為例

嚴 虹

?

連貫性視閾下“代數思維”課程設置的比較研究——以“中”“美”“英”“澳”“新”“南非”六國課程內容為例

嚴 虹

（貴州師范大學 數學科學學院，貴州 貴陽 550001）

代數思維作為代數課程的基礎內容，作為鏈接“算術”與“代數”課程的橋梁，歷來受到國內外數學教育家們的關注．選擇澳大利亞、中國、英國、新加坡、美國、南非作為代表國家，基于課程連貫性視閾，圍繞“代數思維”課程的內容分布、知識主題選擇、設置始末年級、連續性以及邏輯結構等方面進行“小學—初中—高中”國際比較研究，從而審視中國代數思維內容設置的基本特征，以期在全面深化課程改革的大背景下對中國“代數思維”內容的分布情況、內容的選擇與組織有一定的啟示作用．

連貫性；代數思維；課程設置；比較研究；課程標準

1 問題提出

2014年教育部頒布《教育部關于全面深化課程改革落實立德樹人根本任務的意見》，明確指出“統籌小學、初中、高中、本專科、研究生等學段”“要避免有的學科客觀存在的一些內容脫節、交叉、錯位的現象，充分體現教育規律和人才培養規律”；進一步指出“修訂課程方案和課程標準”“要增強整體性，強化各學段、相關學科縱向有效銜接和橫向協調配合”．標志著中國已經全面進入深化課程改革時期．

連貫，字面意思就是“連接貫通”；還有一層意思就是“說話、文章等意思貫通，邏輯清楚”[1]．連貫性，在國內被談及較多的是“教育的一致性和連貫性原則”，這是德育原則之一，中小學之間、初高中之間、中學大學之間、各年級之間，都有銜接問題；種種銜接就必定要求德育工作保持連貫性，從而使學生能在有目的、有計劃、有層次的教育中健康成長[2]．課程連貫性傾向于知識邏輯層面的連接貫通．基于課程連貫性的研究目前在國內并不多見，更多地是以課程編制原則的形式呈現，缺乏微觀層面的深入分析和界定[3-4]．課程連貫性的研究在國外（尤其是美國）多是出現在國家課程的編制過程中，但是仍以質性界定為主[5]．

數學學科歷來皆是各國基礎教育階段的核心課程內容，其中“邏輯性”是其鮮明的學科特征之一．美國2010年發布了《統一核心州數學標準》（）基于數學學科“邏輯性”的基本特征，提出了美國數學課程編制的基本原則“更集中和更具連貫性”．其中，對于內容標準和課程是“連貫的”，給出了描述性的界定：“能夠隨著時間以一系列有邏輯的主題和行為的方式結合在一起，并能恰當地體現學科內容次序性或層次性的本質．”[6]因此，數學課程“連貫性”的要求是結合學科具體特征，同時高于課程編制“銜接性”要求[7]．

綜上所述，研究中所指的課程連貫性主要具有以下特征：一方面，課程內容具有內部整體性（詳見文中“內容分布”“主題選擇”“主題連續性”等內容的探討）；另一方面，課程內容知識在邏輯層面上具有次序性（詳見文中“主題邏輯結構”等內容的探討）．

基于數學課程標準的國際比較研究，近年來國內曹一鳴教授、史寧中教授領銜的團隊均有較為深入的研究．其中，曹一鳴團隊圍繞不同階段（尤其是高中階段）數學課程標準內容分布、理念目標、不同知識單元廣度深度等方面進行了一系列的探討[8-16]；史寧中團隊主要針對高中階段數學課程標準教育理念、主要內容、呈現方式、廣度深度等方面進行了一系列的分析[17-19]．

《義務教育數學課程標準（2011年版）》中指出：“在數學課程中，應當注重發展學生的符號意識．代數思維與算術思維不同，是由關系或結構來描述的，它的目的是發現（一般化）關系、明確結構，并把它們聯系起來．”[20]代數思維是數學科學由常量數學轉向變量數學的里程碑，在數學發展歷史中有著極其特殊的意義．“早在1994年2月，全美數學教師理事會就通過了一個關于‘為每個人的代數（algebra for everyone）’的報告．該報告指出，所有中學生都應該有機會學習代數的基本思想和方法，而學校中的代數教學和學生的成績并不理想．進而，在美國人們開始關注代數思維（algebraic thinking）的教學研究．”[21]2001年12月，國際數學教育委員會第12屆會議（ICMI-12）在澳大利亞墨爾本召開，此次會議專門成立了早期代數工作組，將代數的起步教學作為專門的研究領域．這表明早期代數的研究開始走上了國際舞臺[22]．近年來，國際上關于“早期代數思維”（early algebraic thinking）的研究主要集中在教學維度．比如，拉德福德（Radford）、路易斯（Luis）針對小學生代數思維（從沒有符號到依托符號）的逐漸過渡，開展了一項長達5年的研究調查：研究基于教學的文化—歷史理論，深入剖析了代數思維的組成成分，進而提出在課堂教學中，通過調整教學設計以及指導教學行為，進而有效地促進學生代數思維的發展[23-24]．沃倫（Warren）、伊麗莎白（Elizabeth）提出了一種基于新知識和教育學視角的模型，用于促進幼兒教師早期代數思維的專業學習，以“模式和代數線索”為例，有效協助6位一年級教師憑借自身實力成為專家[25]，等等．而基于課程文本維度的研究尚不多見，早年舒密特（William H. Schmidt）團隊在TIMSS項目課程分析子項目中進行了長達二十余年的研究，主要是基于各個國家課程研制者進行問卷調查，根據調查數據繪制追蹤圖，其中部分內容涉及“代數”內容，但是并未就“代數思維”進行深入分析，且“追蹤圖”具有一定程度上的“主觀性”（并非完全基于課程問題，而是主要基于各國課程研究者對于本國課程的了解程度）[26-28]．

選擇6個國家“小學—初中—高中”整個基礎教育階段的現行數學課程標準文本作為研究對象，以“代數思維”內容為例，首創新型課程研究工具WTTM進行課程連貫性的國際比較研究，以期對中國數學課程深化改革過程中“代數思維”內容的選擇和組織提供一定的參考．

2 研究設計

2.1 研究對象的選取

綜合考慮樣本國家的地域位置、經濟狀況、文化以及數學教育背景等因素，除中國之外選取了5個代表性國家：澳大利亞、英國、新加坡、美國、南非（選取的6個國家以國家代碼首字母進行排序，分別是澳大利亞、中國、英國、新加坡、美國、南非），6個國家基礎教育階段主體學制以及研究選取的國家數學課程標準文本如下（為了全文行文一致，各國均根據學制按年級順序排列）．

表1 樣本國家主體學制及國家課程標準文本

注：英國將11年義務教育分為4個關鍵階段（key stages），國內學界一般將關鍵階段1（year1、year2）和關鍵階段2（year3、yera4、year5、year6）等同于國內小學階段．而對于初中、高中階段的劃分，國內學界存在一定爭議，考慮到數學課程標準的官方性質，參考曹一鳴《十三國數學課程標準評介（高中卷）》一書中的劃分標準，將關鍵階段3（year7、year8、year9）等同于國內初中階段，將關鍵階段4（year10、year11）等同于國內高中階段．

2.2 研究思路與方法

以澳大利亞、中國、英國、新加坡、美國、南非6個國家數學課程標準文本作為研究對象，以“代數思維”課程內容為例，探索“小學—初中—高中”數學課程整體設置的連貫性問題．采用內容編碼、描述統計、比較研究等定性與定量相結合的研究方法，針對TIMSS經典課程分析工具“主題追蹤圖”（Topic Trace Mapping）的主要缺陷：主觀性以及難以凸顯課程重點，首創以課程標準內容條目數量設置權重的研究工具“加權主題追蹤圖”（Weighted Topic Trace Mapping，簡稱WTTM）．通過比較研究，對中國基礎教育階段“代數思維”課程內容的選擇和組織進行分析和探索．

3 連貫性視閾下“代數思維”課程內容的比較研究

該研究在美國實施課程調查（Surveys of Enacted Curriculum，簡稱SEC）項目“K-12數學分類”的基礎上，結合六國數學課程實際情況，經過兩輪次“理論搭建+實踐修正”之后，最終確定“代數思維”內容主題及編碼體系如下：131 未知數、變量的使用；132 代數式概念；133 代數式的運算；134 代數式的證明；130 其它代數思維內容．

在此基礎上，先后將六國“代數思維”相關課程內容條目進行編碼、統計，最終繪制出相應的WTTM如圖1~6．

圖1 澳大利亞代數思維WTTM

圖2 中國代數思維WTTM

圖3 英國代數思維WTTM

圖4 新加坡代數思維WTTM

圖5 美國代數思維WTTM

圖6 南非代數思維WTTM

3.1 內容分布基本情況

就整個基礎教育階段而言，六國代數思維課程內容分布情況如圖7~8所示．

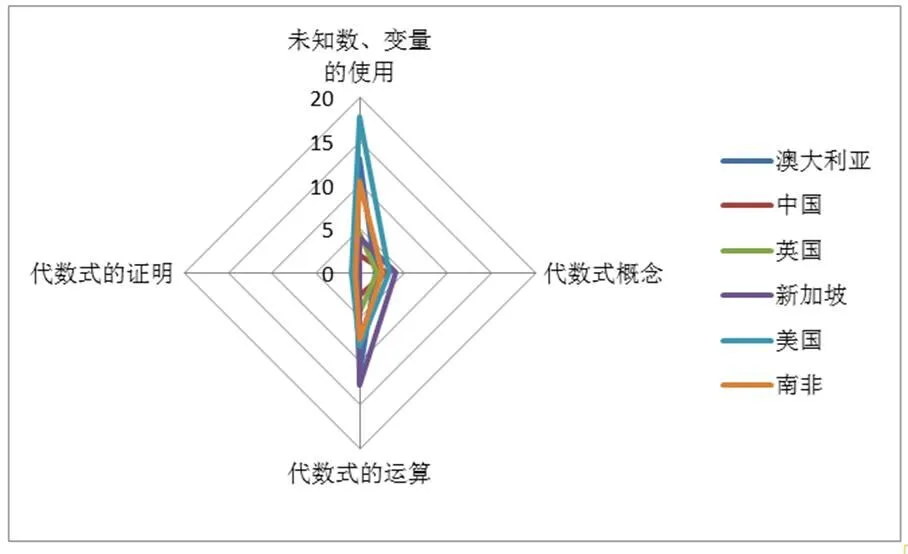
圖7 代數思維主題分布雷達圖

圖8 代數思維主題分布柱形圖

注：各國小學、初中、高中階段有多于一門數學課程的情況，按照平均值統計，比如，澳大利亞高中共有4門數學課程，以4門課程主題數量平均值代表該國高中階段主題數量．

可以看出，對于代數思維內容條目絕對數量而言，美國、澳大利亞內容條目數量較多，中國、英國內容條目數量較少，并且六國主要集中分布在“未知數、變量的使用”“代數式的運算”知識主題上．對于代數思維內容條目相對數量而言，在“未知數、變量的使用”知識主題中，美國所占比重最大（58.48%），新加坡所占比重最小（19.35%）；在“代數式概念”知識主題中，中國所占比重最大（37.50%），澳大利亞所占比重最小（6.54%）；在“代數式的運算”知識主題中，新加坡所占比重最大（61.30%），美國所占比重最小（27.32%）；在“代數式的證明”知識主題中，英國所占比重最大（8.33%），新加坡、南非課程標準文本中沒有出現相關內容條目．

為了更為明晰地了解中國在六國中的基本情況，將中國與六國均值統計如圖9所示．

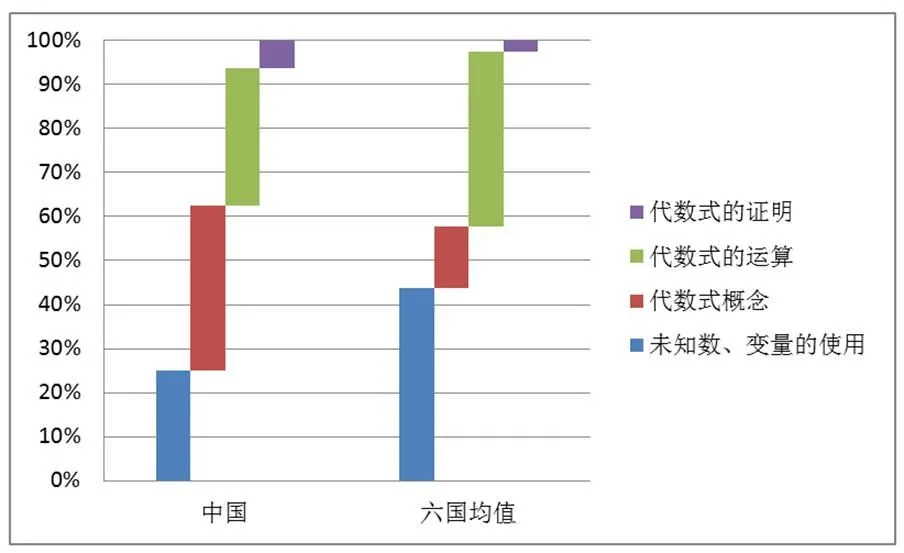
圖9 代數思維主題分布（中國和六國均值）

可以看出，中國在“代數式的運算”“代數式的證明”知識主題所占比重與六國均值較為接近；然而，在“代數式概念”知識主題所占比重（37.50%）明顯高于六國均值（17.20%），同時也是六國中所占比重最大的國家；在“未知數、變量的使用”知識主題所占比重（25.00%）明顯低于六國均值（40.03%）．

3.2 主題選擇比較與分析

從整體上看，六國對于除130（其它代數思維內容）之外其余4個知識主題的覆蓋程度比較全面：澳大利亞、中國、英國和美國，4個知識主題均有涉及；新加坡、南非沒有“代數式的證明”．

另一方面，由于各國不同的文化教育傳統，六國對于“代數思維”在內容選擇上也呈現出一定的差異：澳大利亞從小學一年級開始涉及“數字模式”，高中“專業數學”課程中涉及“推導并使用與帕斯卡三角相關的簡單恒等式”“證明并應用因式定理和余數定理”等“代數式的證明”知識主題．中國從四~六年級開始涉及“用字母表示數”，七~九年級開始涉及“能推導乘法公式，了解公式的幾何背景，并能利用公式進行簡單計算”等“代數式的證明”知識主題．英國從小學六年級開始涉及“代數地表達缺失數的問題”“推導并描述線性數序”，關鍵階段4開始涉及“理解方程和恒等式的不同；數學論證以顯示代數表達式的等值性，并使用代數支持和建立論點{和證明}”等“代數式的證明”知識主題．新加坡從小學六年級開始涉及“用字母表示數”．美國從小學一年級開始涉及“用含一個未知數的等式來表征問題”“算術模型”，高中階段涉及“證明多項恒等式并運用它們描述數字關系”．南非從小學一年級開始涉及“創造和描述自己的模式調查并拓展數字模型以尋找模式的關系或規則”．

對于代數思維“其他”內容，各國不盡相同．澳大利亞涉及表征形式，比如“使用電子表格或同等技術畫表格，記錄公式中的值，包括二維雙向表，如身體質量指數（BMI）表包括不同的體重和身高”．英國涉及表征形式，比如“將建模情形或過程翻譯為代數表達式或公式，并且使用圖表”．美國涉及余數定理．南非涉及余因子定理，比如“重視并理解最多三次多項式的余因子定理；分解三次多項式（包括要求因式分解定理的實例）”．

3.3 主題組織比較與分析

（1）主題最早開始年級和主題最晚結束年級．

依次統計六國代數思維課程內容知識主題最早開始年級以及最晚結束年級，如圖10~11所示．

圖10 六國代數思維知識主題最早開始年級

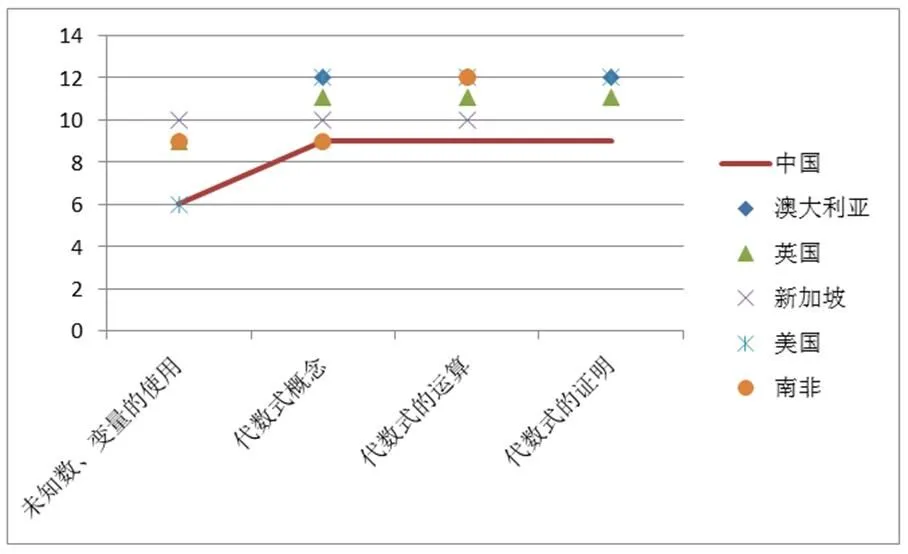
圖11 六國代數思維知識主題最晚結束年級

注：為了更為細致地研究各國基本情況，統計主題早晚年級時，課程標準文本中以“階段”表述的主題，統一將該階段起始年級作為主題的最早開始年級，將該階段結束年級作為主題的最晚結束年級．

可以發現，就知識主題最早開始年級而言，“代數式概念”設置時間較為集中，均在六~八年級開始．“未知數、變量的使用”澳大利亞、美國、南非均從一年級開始設置，英國、新加坡則從六年級開始設置；“代數式的運算”南非從四年級開始設置，澳大利亞、中國從七年級開始設置；“代數式的證明”英國從六年級開始設置，澳大利亞則從十一年級開始設置．相較于六國平均水平，中國在“代數式概念”設置時間與六國一致，“未知數、變量的使用”“代數式的運算”設置時間略晚于六國，“代數式的證明”設置時間略早于六國．

就知識主題最晚結束年級而言，中國在4個知識主題設置時間均明顯前置．相較于六國平均水平，“未知數、變量的使用”“代數式概念”“代數式的運算”“代數式的證明”設置時間較之六國均前置兩年．從一定程度上可以說明中國代數思維課程內容設置時間相對較短．

（2）主題連續性．

分別從兩個方向探索代數思維知識主題的連續性情況，一方面逐一考察每個知識主題的階段（小學、初中、高中）跨度情況，如圖12所示．不難看出，中國是唯一代數思維知識主題全部僅“涉及1個階段”的國家，“未知數、變量的使用”僅涉及小學階段，其余3個知識主題僅涉及初中階段，而英國、新加坡沒有僅“涉及1個階段”的知識主題．澳大利亞、英國、新加坡、美國均有3個知識主題“涉及2個階段”．英國、南非各有一個知識主題涉及小學、初中、高中3個階段，均為“代數式的運算”．從一定程度上可以說明中國代數思維課程內容設置呈現出集中性的特征，是六國之中階段跨度最小的國家．

圖12 代數思維知識主題階段跨度分布

另一方面注意考察每個知識主題的連續情況，如圖13所示．不難看出，中國是唯一代數思維知識主題全部僅“涉及一個年級（階段）的國家”，很大程度上歸因于中國也是唯一小學階段按照學段進行課程內容設置的國家，故無法深入考察知識主題的連續或中斷情況，英國、新加坡沒有僅“涉及一個年級（階段）”的知識主題．英國、新加坡是“年級（階段）間連續”所占比重最大的國家，各有3個知識主題連續．澳大利亞、美國是“年級（階段）間中斷”所占比重最大的國家，各有兩個知識主題中斷．

圖13 代數思維知識主題連續性分布

（3）主題邏輯結構．

為了更為直觀地將中國與六國課程內容設置基本情況進行比較，該研究設計合理算法，將六國課程設置的基本情況進行整合，繪制基于六國代數思維課程內容設置參考模型，如圖14所示．

內容設置參考模型中代數思維知識主題出現的邏輯順序為：“未知數、變量的使用”（一年級）→“代數式的運算”（六年級）→“代數式概念”（七年級）→“代數式的證明”（十一年級）．而中國代數思維知識主題出現的邏輯順序為：“未知數、變量的使用”（第二學段）→“代數式概念”“代數式的運算”“代數式的證明”（第三學段）．

可以看出，在參考模型中，知識主題出現的先后順序層次較為清晰，整個小學階段、初中階段貫穿“未知數、變量的運用”，不斷強化代數思維的滲透，將“算術”與“代數”進行有效銜接；小學結束之前設置“代數式的運算”延續到整個初中、高中階段，從值的“輸入輸出”開始，為之后“代數式概念”做準備；初中階段設置“代數式概念”；高中階段根據實際需要設置“代數式的證明”．

圖14 代數思維課程內容設置參考模型

圖15 中國代數思維課程內容設置

另一方面，關于“代數思維”單元知識主題設置重點．“未知數、變量的運用”知識主題，參考模型中設置時間長，其中，四、五、六、八年級皆為課程重點、次重點；中國僅在四~六年級設置為次重點．“代數式運算”，參考模型在初中階段設置為重點，與中國相同；“代數式概念”，參考模型中沒有將其設置為重點，中國在初中階段設置為重點．“代數式證明”，參考模型與中國皆沒有將其設置為重點．

可以看出，參考模型中重視“未知數、變量的運用”“代數式運算”，而中國則重視“代數式運算”“代數式概念”．

4 啟示與建議

他山之石可以攻玉．通過國際比較研究，可以審視中國代數思維課程內容設置的基本情況，從而為中國基礎教育階段數學課程內容設置趨向“整體性”“連貫性”提供一定參考．

（1）適當增加“未知數、變量的使用”所占比重．中國在“未知數、變量的使用”知識主題所占比重明顯低于六國均值，然而澳大利亞、美國、南非從小學一年級即開始設置相關內容，分別是澳大利亞“模式與代數”、美國“運算與代數思維”、南非“數字模式”模塊，且一直延續到初中階段，同時在參考模型中將其設置為重點．由此可見，“未知數、變量的使用”知識主題作為代數思維的基礎知識，作為“代數式概念”的引導性內容，在國際中得以普遍重視，中國對此知識主題重視程度略顯不足．

（2）適當提前“未知數、變量的使用”“代數式的運算”尤其是“代數式的運算”最早開始年級；適當推后代數思維知識主題最晚結束年級．中國代數思維課程內容階段跨度是六國中最小的國家，所屬4個知識主題均只屬一個階段，連續性較弱；然而，代數思維作為聯系“算術”與“代數”的橋梁，在澳大利亞、英國、美國、南非均橫跨小學、初中、高中3個階段，適當延長中國整個代數思維課程內容的設置時間顯得很有必要．

（3）進一步明晰代數思維單元知識主題出現的邏輯順序．在參考模型中，知識主題出現的先后順序層次較為明晰，整個小學階段、初中階段貫穿“未知數、變量的運用”，將“算術”與“代數”進行有效銜接；小學結束之前設置“代數式運算”延續到整個初中、高中階段；初中階段設置“代數式概念”；高中階段根據實際需要設置“代數式證明”．

[1] 程榮．同義詞大詞典[M]．上海：上海辭書出版社，2010：198．

[2] 林崇德．中國中學教學百科全書·教育卷[M]．沈陽：沈陽出版社，1990：160．

[3] 占小紅，張新宇，范軼．教材“連貫性”評價工具設計及應用[J]．全球教育展望，2010，39（9）：51-56．

[4] 和學新，馬蘇靜．我國基礎教育課程教材開發與管理的問題檢視與改進[J]．教育理論與實踐，2013，33（28）：47-51．

[5] 馬健生，苑大勇．《從先學前班到8年級的課程焦點：追求連貫性》報告述評[J]．比較教育研究，2007，29（5）：48-52．

[6] Common Core State Standards Initiative. Common core state standards for mathematics [EB/OL]. (2016-08-02) [2017-03-29]. http://www.corestandards.org/Math.

[7] 嚴虹．六國基礎教育階段數學課程內容的銜接性研究[J]．數學教育學報，2016，25（4）：63-68．

[8] 康玥媛，曹一鳴．中、澳、芬數學課程標準中內容分布的比較研究[J]．教育學報，2012，8（1）：62-66．

[9] 嚴虹，吳立寶，康玥媛．中美初中數學課程的比較研究[J]．比較教育研究，2015，37（2）：96-101．

[10] 嚴虹．中、新、韓、日四國高中數學課程目標的比較研究[J]．外國中小學教育，2015（1）：60-64．

[11] 曹一鳴，賈思雨．高中平面解析幾何課程設置的國際比較——基于12個國家高中數學課程標準的研究[J]．外國中小學教育，2015（10）：58-65．

[12] 宋丹丹，曹一鳴．高中課程標準中函數內容的國際比較研究[J]．數學通報，2014，53（12）：1-7，16．

[13] 曹一鳴，王萬松．高中概率統計內容設置的國際比較——基于15個國家數學課程標準的研究[J]．數學教育學報，2016，25（1）：1-4．

[14] 曹一鳴，嚴虹．高中數學課程內容及其分布的國際比較——基于12個國家數學課程標準的研究[J]．數學通報，2015，54（7）：9-14．

[15] 曹一鳴，代欽，王光明．十三國數學課程標準評介（高中卷）[M]．北京：北京師范大學出版社，2013：1-6．

[16] 曹一鳴．十三國數學課程標準評介（小學、初中卷）[M]．北京：北京師范大學出版社，2012：1-5．

[17] 史寧中，孔凡哲．十二個國家普通高中數學課程標準國際比較研究[M]．長沙：湖南教育出版社，2013：1-6．

[18] 徐乃楠，孔凡哲，史寧中．俄羅斯高中數學教育標準、示范性大綱和教科書的最新變化特征及啟示[J]．全球教育展望，2015，44（1）：100-109．

[19] 呂世虎，史寧中，陳婷．《標準》與《大綱》中幾何部分內容難度的比較研究[J]．課程·教材·教法，2006，26（8）：38-43．

[20] 徐文彬．試論算術中的代數思維：準變量表達式[J]．學科教育，2003（11）：6-10，24．

[21] ?KRIEGLER S. Just what is algebraic thinking submitted for algebraic concept in the middle school [J]. A Special Edition of Mathematics: Teaching in the Middle School, 1994 (5): 1-10.

[22] 劉久成，劉久勝．代數思維及其教學[J]．課程·教材·教法，2015，35（12）：76-81．

[23] ?RADFORD, LUIS. The progressive development of early embodied algebraic thinking [J]. Mathematics Education Research Journal, 2014, 26 (2): 257-277.

[24] ?RADFORD, LUIS. On the development of early algebraic thinking [J]. PNA, 2012, 6 (4): 117-133.

[25] WARREN, ELIZABETH. Early childhood teachers’ professional learning in early algebraic thinking: a model that supports new knowledge and pedagogy [J]. Mathematics Teacher Education and Development, 2008 (10): 30-45.

[26] ?WILLIAM S. Survey of mathematics and science opportunities (curriculum analysis technical report series No.5 general topic trace mapping: data collection and processing) [M]. East Lansing: Michigan State University, 1995: 10-12.

[27] ?SCHMIDT W H, WANG H C, McKNIGHT C C. Curricular coherence: an examination of US mathematics and science content standards from an international perspective [J]. Curriculum Studies, 2005, 37 (5): 525-559.

[28] ?SCHMIDT W H, PRAWAT R S. Curriculum coherence and national control of education: issue or non-issue [J]. Journal of Curriculum Studies, 2006, 38 (6): 641-658.

[29] ?ACARA. The Australian curriculum: mathematics f-12 version 7.2 [EB/OL]. (2016-08-03) [2017-03-19]. http://www. australiancurriculum.edu.au/Curriculum/Overview.

[30] ?ACARA. The Australian curriculum: mathematics senior secondary version 7.2 [EB/OL]. (2016-08-03) [2017-03-19]. http://www.australiancurriculum.edu.au/SeniorSecondary/Overview.

[31] 康玥媛．澳大利亞全國統一數學課程標準評析[J]．數學教育學報，2011，20（5）：81-85．

[32] 董連春，Max Stephens．澳大利亞全國統一高中數學課程標準評述[J]．數學教育學報，2013，22（4）：16-20．

[33] 中華人民共和國教育部．義務教育數學課程標準（2011年版）[M]．北京：北京師范大學出版社，2012：16-41．

[34] 中華人民共和國教育部．普通高中數學課程標準（實驗）[M]．北京：人民教育出版社，2003：12-65．

[35] ?Department of Education. National curriculum in England: mathematics programmes of study [EB/OL]. (2016-03-09) [2017-08-03]. https://www.gov.uk/government/publications/national-curriculum-in-england-mathematics-programmes- of-study.

[36] 徐文彬，楊玉東．英國國家數學課程標準的確立與變革及其啟示[J]．數學教育學報，2002，11（3）：48-51．

[37] Singapore Examinations and Assessment Board. Mathematics syllabus [EB/OL]. (2016-11-03) [2017-03-19]. https://www.seab.gov.sg/pages/nationalExaminations/PSLE/general_information.asp.

[38] 寧連華，崔黎，金海月．新加坡高中數學課程標準評介[J]．數學教育學報，2013，22（4）：1-5．

[39] 張守波．新加坡高中數學教學大綱的特色與啟示[J]．數學教育學報，2013，22（6）：58-61．

[40] Common Core State Standards Initiative. Common core state standards for mathematics [EB/OL]. (2017-03-29) [2017-08-03]. http://www.corestandards.org/Math.

[41] 曹一鳴，王立東，Paul Cobb．美國統一州核心課程標準高中數學部分述評[J]．數學教育學報，2010，19（5）：8-11．

[42] 廖運章．美國《州共同核心數學標準》的內容與特色[J]．數學教育學報，2012，21（4）：68-72．

[43] ?CAPS. Curriculum and assessment policy statement foundation phase mathematics [EB/OL]. (2016-11-03) [2017-03-19]. http://www.education.gov.za/Curriculum/NCSGradesR12/CAPS/tabid/420/Default.aspx.

[44] 李娜，曹一鳴，Lyn Webb．南非國家高中數學課程與評價標準評介[J]．數學教育學報，2013，22（4）：6-10．

An International Comparative Study about Curriculum Content Settings of Algebraic Thinking Based on Coherence Visual Threshold——Take the Curriculum Content of China, United States, United Kingdom, Australia, Singapore and South Africa for Example

YAN Hong

(School of Mathematics Science, Guizhou Normal University, Guizhou Guiyang 550001, China)

The “Algebraic Thinking” was the basic content of Algebra Curriculum, which was the bridge connected “arithmetic” and “Algebra”. Many mathematical educators at home and abroad always were focus on this problem. This study chose behalf of the state such as Australia, China, United Kingdom, Singapore, United States and South Africa. From the coherence visual threshold, the international comparative study revolves “Algebraic Thinking” content, for content distribution, topic selecting, setting time, continuous, and logical structure, which studies from primary school, junior high school to senior middle school. And it got some basic characteristics about curriculum settings of “Algebraic Thinking” in our country. The study took some inspiration for the distributed situation, the choice and organization of content for our country curriculum.

curriculum coherence; algebraic thinking; curriculum settings; comparative study; curriculum standards

G40-059.3

A

1004–9894（2018）06–0060–07

嚴虹．連貫性視閾下“代數思維”課程設置的比較研究——以“中”“美”“英”“澳”“新”“南非”六國課程內容為例[J]．數學教育學報，2018，27（6）：60-66．

2018–06–29

2015年度教育部人文社會科學研究項目——基于課程連貫性視閾的基礎教育階段數學課程國際比較研究（15YJC880104）；天津市教育科學“十三五”規劃課題——“幼小”“小初”學段銜接的課程建設實踐研究（BE3330）

嚴虹（1980—），女，江蘇南京人，教授，博士，主要從事數學教育和數學課程國際比較研究．

[責任編校：周學智、張楠]