50ETF隱含波動率曲面實證研究和統(tǒng)計套利

1.背景介紹與文獻綜述

1.1 50ETF 和 50ETF 期權(quán)

現(xiàn)代期權(quán)產(chǎn)品從四十年前第一次在芝加哥期權(quán)交易所上市以來，已經(jīng)在歐美形成了較大的市場規(guī)模，對期權(quán)的研究到目前為止在歐美也出版了大量文章。但中國的期權(quán)市場起步相對較晚，國內(nèi)第一只場內(nèi)交易期權(quán)— 50ETF 期權(quán)產(chǎn)品，在 2015 年才在上海證券交易所上市交易，因此對于國內(nèi)期權(quán)的研究也相對較少，主要研究內(nèi)容也集中于期權(quán)的定價模式，對隱含波動率的研究較少。基于以上事實，本文從實證檢驗角度出發(fā)，探究 50ETF 期權(quán)產(chǎn)品隱含波動率曲面所滿足的經(jīng)驗法則，并針對隱含波動率的均值回歸特性，嘗試開發(fā)基于交易隱含波動率的期權(quán)策略。50ETF 交易量較大，從 2005 年至今，平均的每日交易合約數(shù)超過 4 億，交易日超過3000個。在中國是一支比較活躍的基金，以其作為標的資產(chǎn)的 50ETF 期權(quán)也吸引很多投資者的關(guān)注。因此研究 50ETF 期權(quán)的交易策略和其期權(quán)本身的性質(zhì)是一個有意義的課題。

1.2 隱含波動率模型

許多學(xué)者對隱含波動率性質(zhì)進行了研究，一方面，實現(xiàn)波動率不能全面反映期權(quán)信息，基于市場模擬數(shù)據(jù)指出，由于隱含波動率的變化，股票價格的變化不會全部體現(xiàn)在期權(quán)價格上，另一方面，經(jīng)典的 期權(quán)定價模型得到的歐式期權(quán)價格與市場實際數(shù)據(jù)出現(xiàn)背離。根據(jù)市場實際數(shù)據(jù)得到二維“波動率微笑” 和“波動率期限結(jié)構(gòu)” 。提出了隨機跳躍模型刻畫標的資產(chǎn)價格游走，但實際效果不佳。隨后研究了一類局部波動率模型。但IVF 模型不能有效表現(xiàn)市場價格的動態(tài)變化。后期提出了 SABR 模型，是一類更加符合市場特征的隱含波動率曲面動態(tài)模型。同時也有很多學(xué)者建立了隱含波動率實證模型，提出了粘性行權(quán)價規(guī)則和粘性 Delta 規(guī)則，對上述兩種規(guī)則進行了進一步檢驗，并提出了時間平方根規(guī)則。構(gòu)建和驗證股票期權(quán)指數(shù)的波動曲面最相關(guān)的經(jīng)驗觀察。國內(nèi)學(xué)者近年來也在這方面有一些研究，這些研究都是基于權(quán)證的數(shù)據(jù)進行的理論研究，但是對于實際市場中的 50ETF 期權(quán)波動率的研究還較少，所以本文針對 50ETF 期權(quán)的隱含波動率是否服從經(jīng)驗規(guī)則進行實證檢驗。

2.數(shù)據(jù)說明

2.1 數(shù)據(jù)的總體說明

圖1 50ETF 期權(quán) 2015-2017 每月活躍交易期權(quán)品種數(shù)量變動

本次實證檢驗的數(shù)據(jù)基于 50ETF 認購與認沽期權(quán)及其對應(yīng)的標的資產(chǎn)50ETF。本文中采用的 50ETF 期權(quán)數(shù)據(jù)(圖1)是從 2015 年 2 月 10 日到 2017 年 8 月 14 日的每日數(shù)據(jù)，50ETF 數(shù)據(jù)是從 2005 年 2 月 24 日到 2017 年 8 月 14 日的每日數(shù)據(jù)，篩選前，50ETF 期權(quán)數(shù)據(jù)共有 63，326 個觀測，50ETF 數(shù)據(jù)共有 3，035 個觀測。本問主要數(shù)據(jù)還包括 50ETF 每日收盤價，實現(xiàn)波動率，日成交量，回報率；50ETF期權(quán)的期權(quán)隱含波動率，希臘值，到期日，行權(quán)價。

2.2 數(shù)據(jù)的細節(jié)說明

為保證數(shù)據(jù)有效性，剔除可能存在的由數(shù)據(jù)導(dǎo)致的偏差，本文采用了一些篩選數(shù)據(jù)的標準，它們包括：(1)被考慮的數(shù)據(jù)其合約據(jù)到期日應(yīng)該至少有 6 個交易日，并且為了保證流動性，合約據(jù)到期日的時間不應(yīng)該超過 1 年(以交易日計算)，(2)根據(jù) Dumas(1997) 提出的標準，被考慮的數(shù)據(jù)對應(yīng)的絕對在值程度浮動應(yīng)該不超過 10%，絕對在值程度由下式給出：

M*=期權(quán)的行權(quán)價/對應(yīng)標的資產(chǎn)當日價格-1

在應(yīng)用以上標準(1)后，篩選得到的數(shù)據(jù)包含59，852個觀測，(表1)給出了僅應(yīng)用了篩選標準(1)后的數(shù)據(jù)分布情況，其中：

M=期權(quán)的行權(quán)價/對應(yīng)標的資產(chǎn)當日價格

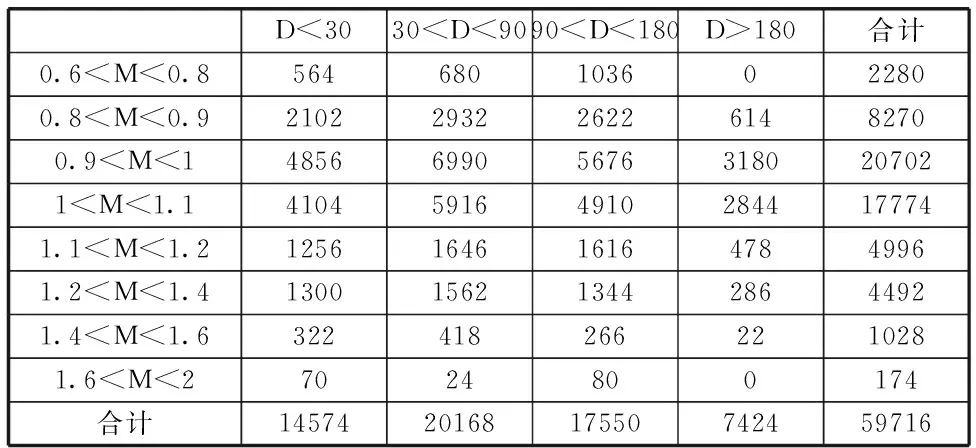
表1 50ETF 期權(quán)數(shù)據(jù)說明，通過在值程度(M)與到期日時長(D)分類，不等號在不等式右側(cè)取等

*M 計算方式如上文

3.50ETF隱含波動率曲面擬合模型

隱含波動率曲面經(jīng)驗法則主要分為兩類，第一類是波動率曲面位移隨時間變化的經(jīng)驗法則，第二類是不同成熟期的期權(quán)在某一時點的波動率 ‘微笑’。本文使用了三種不同的經(jīng)驗法則，分別是粘性行權(quán)價規(guī)則，粘性 Delta 規(guī)則，時間平方根規(guī)則，前兩者屬于第一類經(jīng)驗法則，最后一條則屬于第二類經(jīng)驗法則。

考慮歐式的看漲期權(quán)，它的成熟期是 T，行權(quán)價是 K，它的隱含波動率是一個關(guān)于T和K的函數(shù)，記為σTK。同時我們定義期權(quán)的價格為c(對應(yīng)的，看跌期權(quán)記為p)，標的資產(chǎn)的價格為S，希臘值Δ：=dc/dS(或dp/dS)。

3.1 粘性行權(quán)價規(guī)則

假設(shè)σTK與標的資產(chǎn)價格S是兩個獨立隨機變量，而c和p是一個與S，σTK以及從現(xiàn)階段到到期日的時間T-t有關(guān)的函數(shù)，根據(jù)Derman(1997)，粘性行權(quán)價規(guī)則可以表述為：

σTK(K，T)=σT+ΔT，K(K，T)=f0(K，T)

這個模型保持了隱含波動率曲面不會隨著T的變化而變動，也不會受到標的資產(chǎn)價格變動的影響，對行權(quán)價K具有“粘性”。但考慮到市場的實際情況，由于每時每刻都有大量的交易存在，使得期權(quán)市場上的期權(quán)具有很多不同的行權(quán)價以及到期日，因此實際運用中往往使用T-t代替T。此時，模型表示隱含波動率曲面的變動與到期日無關(guān)，而與T-t和K有關(guān)，對上面的一個模型采用多項式擬合的方法，使用多元 Taylor 展開，初始模型設(shè)為：

取二階展開得到：

f(K，T)=a0+a1K+a2K2+a3(T-t)+a4(T-t)2+a5K(T-t)+ε

(2)

作為一個回歸模型，假設(shè)其滿足 Gauss-Markov 假設(shè)前提，即模型不具有異方差性以及自相關(guān)性，進行面板數(shù)據(jù)回歸，發(fā)現(xiàn)對全部數(shù)據(jù)的回歸結(jié)果表明擬合優(yōu)度僅有 0.273。但是 D-W 統(tǒng)計量的值僅有 0.202，模型的內(nèi)生變量有自相關(guān)性，因此不接受該模型。使用差分法進行調(diào)整，將所有解釋變量X構(gòu)成一個列滿秩矩陣，并用期權(quán)合約進行行分塊，指標記為k，被解釋變量Y設(shè)為一個列向量，并用期權(quán)合約進行行分塊，指標記為k，進行下述差分變換：

(3a)

(3b)

其中變換的系數(shù)設(shè)為1-0.5DW，重新進行回歸分析，得到新的可決系數(shù)為 0.083模型不具備較好的解釋效力。該模型差分前的回歸結(jié)果同樣也印證了一些實際觀測結(jié)果，如下圖 (圖2)，該模型對認購和認沽期權(quán)分開進行面板回歸得到的結(jié)果也不盡人意，雖然調(diào)整后滿足 G-W 假設(shè)前提，但是可決系數(shù)都低于 0.1，總體來說粘性行權(quán)價模型不適用于 50ETF 期權(quán)，并且對該模型，差分的方法也缺少實際解釋。

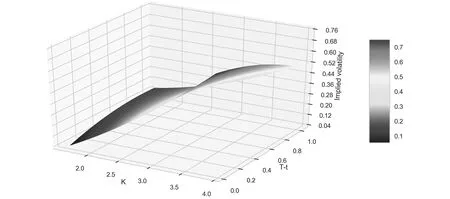
圖2 基于粘性行權(quán)價規(guī)則的 50ETF 期權(quán)擬合波動率曲面

3.2 粘性 Delta 規(guī)則

假設(shè)σTK是一個與標的資產(chǎn)價格S不相獨立的一個隨機變量。此時如果隱含波動率是一個關(guān)于行權(quán)價K的遞減函數(shù)，則隱含波動率是一個關(guān)于標的資產(chǎn)價格S的遞增函數(shù)，同時Δ將會大于B-S公式給出的理論值。換句話說，在這一假設(shè)下，對某一呈現(xiàn)U型波動率微笑曲線的資產(chǎn)，B-S公式在K較低時低估了Delta值，而在K較高時高估了Delta值。它可以被描述為：

σTK-ATM(M，T)=σT+ΔT，K，ATM(M，T+ΔT)=f0(M，T)

即在在值程度M刻畫下，期權(quán)的隱含波動率與在值波動率之差或其比值是一個不隨T變動的量。使用ln(K/F)刻畫在值程度，粘性 Delta 規(guī)則的一種表述運可以是：

σTK-σTF=ψ(M，T-t)=b0+b1ln(K/F)+b2ln2(K/F)+b3(T-t)+b4(T-t)2+b5(T-t)ln(K/F)+ε

(4)

但對于面板回歸的結(jié)果并不理想，考慮到隱含波動率曲面的形狀，在原假定下，增加一項在值程度示性函數(shù)，方程設(shè)為：

σTK-σTF=ψ(M，T-t) +b6I{K/F：K/F>=1}ln(K/F)

(5)

為了消除自相關(guān)性，仍采用與上文相同的處理辦法，處理后面板數(shù)據(jù)總體，認購期權(quán)，認沽期權(quán)均不呈現(xiàn)顯著自相關(guān)性，對于面板全體數(shù)據(jù)，回歸的結(jié)果顯示在 95% 的置信水平下可決系數(shù)為 0.343。對于認購期權(quán)，回歸的結(jié)果顯示在 95% 的置信水平下可決系數(shù)為 0.259；對于認沽期權(quán)，回歸的結(jié)果顯示在 95% 的置信水平下可決系數(shù)為 0.542。顯然，粘性 Delta 規(guī)則就 50ETF 期權(quán)市場而言，相比粘性行權(quán)價規(guī)則，更有解釋效力，但解釋效力仍然有限。

3.3 時間平方根規(guī)則

平穩(wěn)時間平方根規(guī)則由 Natenberg(1994) 和 Hull(2006) 提出，模型假設(shè)隱含波動率由以下關(guān)系式確定：

出于數(shù)值計算上的便利，上式的比值形式可以做稍許修改，因此模型也可以表述為：

利用多元函數(shù) Taylor 公式：

(12)

基于全體數(shù)據(jù)面板，認購期權(quán)數(shù)據(jù)和認沽期權(quán)數(shù)據(jù)的回歸結(jié)果得到四次展開對于該問題存在過擬合現(xiàn)象，如下表(表2)：

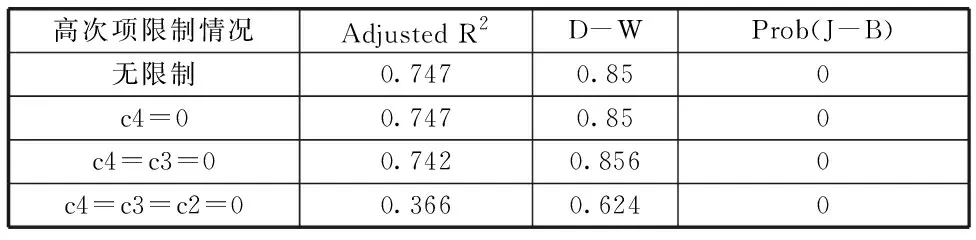
表2 平穩(wěn)平方時間反比規(guī)則回歸結(jié)果：面板數(shù)據(jù)限制高次項

因此，將方程(12)設(shè)為：

(13)

模型變量間呈現(xiàn)正相關(guān)性，故分別對全體面板數(shù)據(jù)，認沽期權(quán)以及認購期權(quán)數(shù)據(jù)回歸時分別采取同上差分修正，發(fā)現(xiàn)對于面板全體數(shù)據(jù)，回歸的結(jié)果顯示在 95% 的置信水平下可決系數(shù)為 0.610，對于認購期權(quán)，回歸的結(jié)果顯示在 95% 的置信水平下可決系數(shù)為 0.573，對于認沽期權(quán)，經(jīng)過嘗試之后使用方程 (12)，回歸的結(jié)果顯示在 95% 的置信水平下可決系數(shù)為 0.714。但是注意到，方程 (12) 中所有系數(shù)均是常數(shù)，因此被稱為是固定系數(shù)的平方反比時間根規(guī)則，但實際上，取方程 (12) 的帶有三次項形式使用由均值回歸檢驗(在下文)得到的均值回歸半衰期進行 11 天的滾動回歸，用 11 天的樣本內(nèi)數(shù)據(jù)估計第 12 天的樣本外數(shù)據(jù)(這里的天并不指日歷日序列，而是滿足篩選條件的交易日序列)，可以發(fā)現(xiàn)，系數(shù)并非固定系數(shù)的的，而是波動 (圖5) 的，因此實際上，方程 (12) 的三次項形式應(yīng)該被表述為：

(15)

但是從 RMSE 結(jié)果來看，11天滾動回歸得到RMSE均值為0.0438，即在RMSE的度量下，誤差不超過 4.4%，是一個可以接受的誤差結(jié)果，因此使用固定系數(shù)時間平方根規(guī)則進行預(yù)測是可行的。

在這一部分中對粘性行權(quán)價規(guī)則的方程進行差分缺少實際意義，因為差分后的變量主要就是對時間T和行權(quán)價K進行的一次放縮，唯一有意義的差分體現(xiàn)在對K和T混合因子的差分上，結(jié)合模型的擬合效力，認為粘性行權(quán)價規(guī)則不適用于50ETF期權(quán)；對于粘性Delta規(guī)則，通過加入一個在值程度示性函數(shù)，強化了模型對于隱含波動率曲面的擬合效力，而模型的差分主要表現(xiàn)為時間效力對波動率差值的復(fù)合影響，最后得到的擬合結(jié)果對認沽期權(quán)較優(yōu)，對認購期權(quán)表現(xiàn)一般；時間平方反比規(guī)則的差分同樣表現(xiàn)了時間效力對于波動率差值的復(fù)合影響，并且在最后的結(jié)果上，對于認購和認沽期權(quán)都獲得了較好的擬合效力，綜上，認為時間平方反比規(guī)則最適合表現(xiàn)50ETF期權(quán)市場的隱含波動率。

4.波動率時間序列性質(zhì)檢驗

這一部分將會檢驗波動率時間序列的均值回歸性。該性質(zhì)使得預(yù)測波動率相較于預(yù)測標的資產(chǎn)價格走勢更可靠。此處利用統(tǒng)計中的假設(shè)檢驗來確定期權(quán)和標的資產(chǎn)的波動率是否服從均值回歸性并同時估算了其時間序列的穩(wěn)定性與均值回歸的周期。

4.1 均值回歸性檢驗

如果波動率序列滿足均值回歸性質(zhì)，也就是若當前波動率呈現(xiàn)遠離均值的趨勢，那么下一階段的波動率就會表現(xiàn)出回歸均值的特性，因此用如下線性模型來表現(xiàn)均值回歸性：

Δxt=μ+θxt+βt+α1Δxt-1+α2Δxt-2+…+αpΔxp+εt

(19)

其中Δxt=xt+1-xt，且μ，θ，β，αi(1≥i≤p)為常數(shù)，使用ADF檢驗(單位根檢驗)的方法，零假設(shè)設(shè)為：

H0∶θ=0

進一步假設(shè)β=0，這指在現(xiàn)實中，波動率是幾乎不帶時間趨勢的，同時取p=1就已經(jīng)足夠完成顯著性檢驗。對于50ETF期權(quán)，檢驗的時間序列為其30天的在值隱含波動率時間序列，若交易日當天不存在恰好為30天到期的期權(quán)，則通過線性插值獲得30天在值隱含波動率數(shù)值。這里分別對50ETF的實現(xiàn)波動率和50ETF期權(quán)在值隱含波動率進行均值回歸檢驗，結(jié)果如下表(表4)

表4 對50ETF的實現(xiàn)波動率和50ETF期權(quán)隱含波動率均值回歸性檢驗結(jié)果

表明在 99%的置信水平下，50ETF標的資產(chǎn)的實現(xiàn)波動率都服從均值回歸過程，但是數(shù)據(jù)檢驗表明，到2015年7月1日為止的部分期權(quán)數(shù)據(jù)并不符合均值回歸過程，僅有從2015年7月1日開始的期權(quán)數(shù)據(jù)服從均值回歸過程，此外還必須估計均值回歸的強度，也就是在期望意義下，估算均值回歸的速度(所消耗的時間)。對方程(19)稍做變形，忽略忽略漂移項βt以及P個滯后差分項就可以將(19)轉(zhuǎn)化成一個典型的O-U過程，并且由假設(shè)檢驗θ=0顯著，因此：

簡單計算半衰期(在期望意義下)為：

最后為了估算θ，引入如下離散的O-U過程：

Δxt=μ+θxt+εt

通過OLS方法進行線性擬合，代入可得：Δt≈10.7805。

5.基于波動率時間序列性質(zhì)的交易策略

在這一部分中，基于Delta中性的方法，探索50ETF和50ETF期權(quán)的交易策略和收益。本文所涉及的交易策略僅針對認購期權(quán)，6.1設(shè)計了一個每日Delta對沖的對比策略用于比對。本文設(shè)置的建倉與平倉條件有兩類，一個是在使用10天移動平均的情況下，隱含波動率偏離均值高于2個標準差和隱含波動率偏離均值低于0.5個標準差作為建倉平倉條件。另一個是在使用11天移動平均的情況下，隱含波動率偏離均值高于2個標準差和隱含波動率偏離均值低于0.75個標準差作為建倉平倉條件。

5.1 對比策略：每日Delta對沖的策略模型

根據(jù)B-S公式，標的資產(chǎn)的Delta恒等于1，因此通過同時操作標的資產(chǎn)和期權(quán)可以使得 Delta為零從而達到控制風(fēng)險的目的，但是在實際操作中，一直保持Delta中性是困難的，因在這里只采用每日的數(shù)據(jù)，主要是收盤時的Delta值，收盤時的期權(quán)價格和收盤時的標的資產(chǎn)價格，這里的所有數(shù)據(jù)均為原始數(shù)據(jù)，只拋棄了缺少數(shù)值的數(shù)據(jù)點，沒有設(shè)置止損策略。每天都進行Delta對沖，(圖3)反映了這樣一種策略的收益率波動和出現(xiàn)各個值段收益率的直方圖以及每天所執(zhí)行的Delta對沖的次數(shù)，并用PnL來表示損益。

圖3 50ETF期權(quán)Delta對沖對比策略收益率波動，出現(xiàn)各個值段收益率的直方圖以及每天所執(zhí)行的Delta對沖的次數(shù)

5.2 基于均值回歸的Delta對沖策略

下面描述了一種改進的Delta對沖策略，在隱含波動率滿足某些條件下進行操作，看多或者看空隱含波動率。在這一部分，對于認購期權(quán)而言，如果看多隱含波動率，就是要通過賣出股票，買入期權(quán)實現(xiàn)Delta中性；而看空隱含波動率恰恰相反。必須要注意的是，這里忽略了融券利率以及賣出期權(quán)之后維持倉位所需要的費用。

表5 Delta 對沖交易策略：建倉平倉條件

分別對全部數(shù)據(jù)和2015年7月1日之后的數(shù)據(jù)進行了考慮，(表5)描述了衡量隱含波動率是否被高估或者低估的條件(建倉和平倉的條件)。(圖4)分別描述了2015年，2015年初到2015年7月1日，從2015年7月1日到2015年年末，2016年，2017年以及整個從2015年年初到2017年的收益率(年化)變動情況，從中可以發(fā)現(xiàn)，2016年是合并所有認購期權(quán)合約后整體收益率最高的一年，而從長期來看，沒有實行任何止損策略的基于Delta中性的交易隱含波動率策略綜合收益接近0。

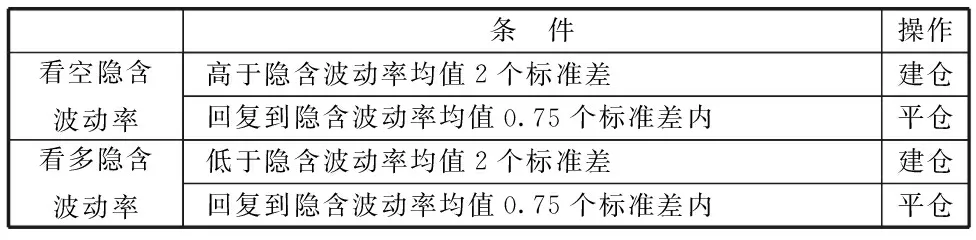
表6 基于滿足隱含波動率均值回歸性時段的delta對沖交易策略：建倉平倉條件

但是如果僅從2015年7月1日向后執(zhí)行策略，并采用第二種交易標準：隱含波動率偏離均值低于0.75個標準差作為建倉平倉條件(表6)，那么策略的整體表現(xiàn)會有較大提升。

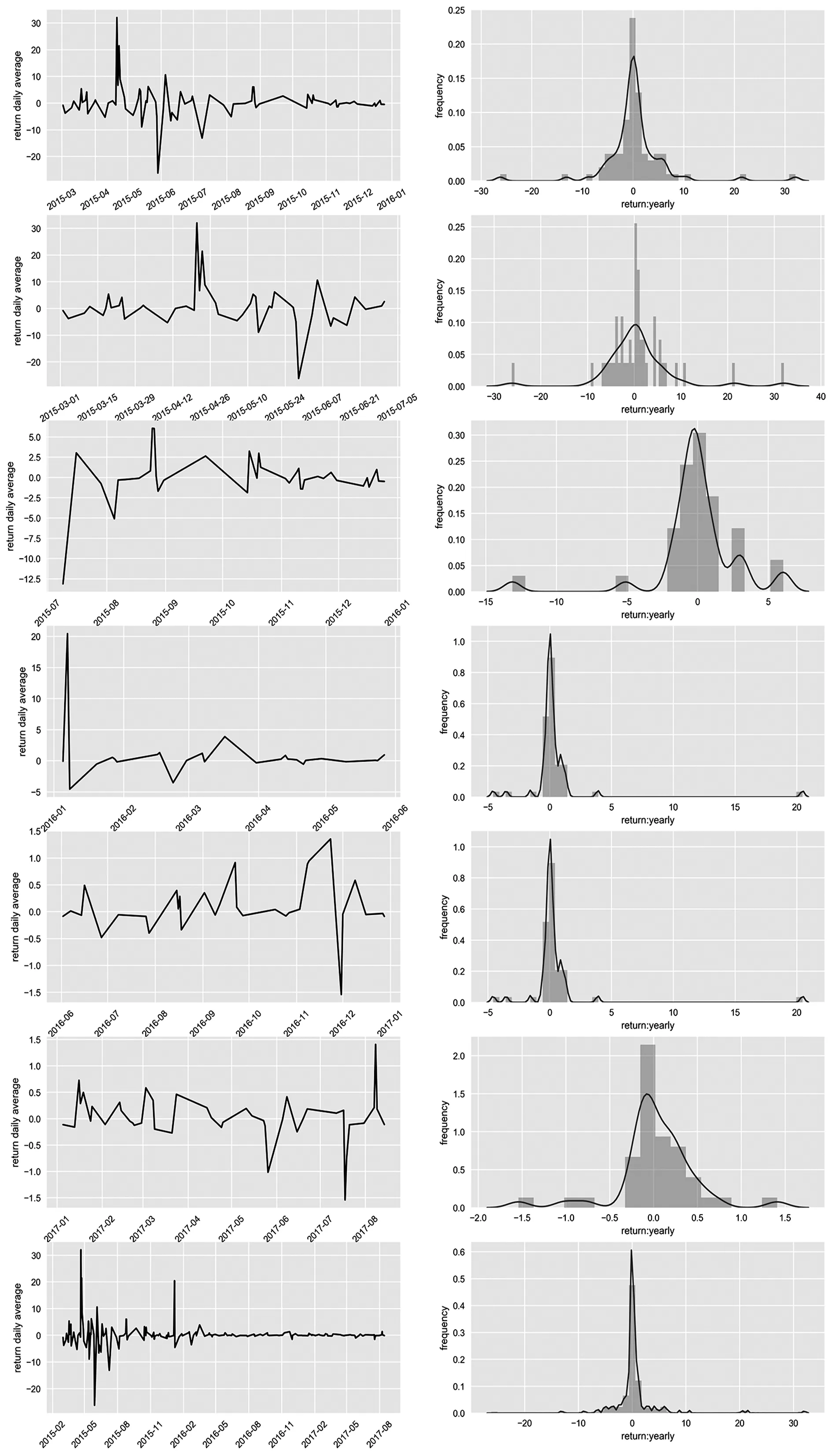
圖4 2015年，2015年初到2015年7月1日，從2015年7月1日到2015年年末，2016年年初到2016年6月1日，2016年6月1日到2016年末，2017年以及從2015年年初到2017年的日平均收益率(年化)變動和對應(yīng)直方圖，假設(shè)市場無風(fēng)險利率為4%，則對應(yīng)的夏普比率分別為：-0.042，-3.155，3.547，1.084，0.302，-3.622，0.031

勝率(盈利的概率)綜合年化收益率Sharpe比率累計PnL0.57160.70842.73323.9076

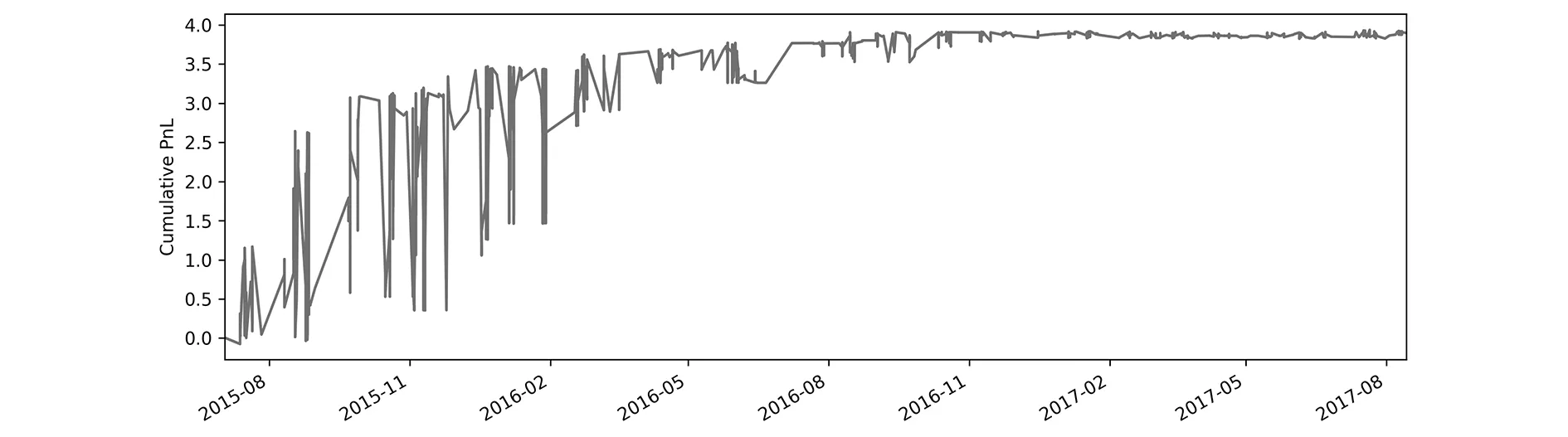
圖5

由(表7)發(fā)現(xiàn)，如果不在序列滿足均值回歸性的時段執(zhí)行Delta中性策略，在短期可以獲得可觀的利潤，2016年的整體年收益率超過20%，但從長期來看，整體收益率難以保證穩(wěn)定，整體年收益率較低。但是如果考慮時間序列的均值回歸性，可以大幅度改善整體策略收益的穩(wěn)定性和最終的結(jié)果。

這里設(shè)計的一組交易策略還存在一些問題，比如在實際操作中，為了進一步改善收益率，減少風(fēng)險，可以采取包括整體資金止損策略和控制頭寸等方法，并且該策略交易強度也不足夠，還存在改善余地。

6.總結(jié)

本文通過回歸模型擬合50ETF隱含波動率并基于其均值回歸性質(zhì)開發(fā)交易策略，在擬合隱含波動率曲面的過程中，比較發(fā)現(xiàn)，時間平方反比規(guī)則比較適用于50ETF期權(quán)市場，又參照機器學(xué)習(xí)中的嶺回歸優(yōu)化方法并使用多項式回歸，發(fā)現(xiàn)時間平方反比規(guī)則依舊具有最好的預(yù)測性能，據(jù)此可以認為時間平方反比模型的確比較適合擬合50ETF期權(quán)的隱含波動率曲面。接下來，本文使用OU過程，檢驗發(fā)現(xiàn)2015年7月以來的在值隱含波動率服從均值回歸性，均值回歸過程的半衰期為10-11天，并基于此開發(fā)了Delta對沖的交易策略，在加入對序列均值回歸性的考察后，僅對2015年7月1日之后的序列使用基于delta對沖的交易策略，使用2倍移動標準差和0.75倍移動標準差作為開倉和平倉條件，收益大幅度改善，夏普比例超過2，年化收益率超過70%，策略勝率為57%，策略表現(xiàn)獲得了較好的改善，也就是說，基于均值回歸性的Delta對沖策略的確可以在市場上獲得一定的收益。

(武漢大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院，湖北 武漢 430072)