高動態環境下聯合開環捕獲和閉環跟蹤的載波同步算法

韓春雷, 白瀅鈺, 司江勃

(1.中國電子科技集團公司 第二十研究所, 陜西 西安 710068; 2.西安郵電大學, 陜西 西安 710100;3.西安電子科技大學, 陜西 西安 710071)

在高動態環境中，通信雙方之間的高速相對運動往往會在接收機接收信號上引入較大的多普勒頻率及其高階變化率。為了適應高動態環境，捕獲和跟蹤接收信號中的多普勒頻率及其變化率，就必須加寬中低動態接收機載波跟蹤環路的環路帶寬。然而環路帶寬的加大勢必降低載波跟蹤精度，當跟蹤環路處于低信噪比通信環境中時尤為如此。噪聲的引入甚至會導致載波跟蹤環失鎖。因此，在動態適應力和跟蹤精度之間的權衡，一直吸引著許多學者進行深入的研究。 高動態環境下常用的跟蹤技術包括基于Kalman濾波器的跟蹤技術、基于最大似然的跟蹤環技術以及基于鎖頻環(FLL)輔助的鎖相環(PLL)技術等等。其中，基于Kalman濾波器的跟蹤方法通過自適應地調整環路參數對載波相位差、多普勒頻率及其變化率進行估計。然而，由于高動態環境對系統穩定性的影響較大，該方法無法實現快速捕獲[1-2]。基于最大似然輔助的環路跟蹤算法是一種漸進無偏估計，其參數的估計方差接近于Cramer-Rao下界(CRLB)，但由于進行二維或三維搜索所需的存儲量和計算量很大，導致算法跟蹤速度變慢[3-4]。在FLL輔助PLL的結構中，FLL和PLL分別用作載波參數的同步和細同步，并由PLL決定最終的跟蹤精度。這種方法的結構相對簡單，但由于FLL環路帶寬較大，引入附加的噪聲功率，降低了跟蹤精度[5]。為了解決這些問題，本文提出了一種聯合開環捕獲和閉環跟蹤的高動態載波同步算法。即通過開環階段能夠實現快速捕獲，同時通過PLL實現高精度載波跟蹤。該算法不僅具有較高動態適應能力，也具有較大的多普勒頻率及其變化率的估計范圍。本文的貢獻有以下2點：①適用于高動態通信環境的線性頻率變化情況；②估計范圍大，精度高。

1 系統模型

接收機的結構框圖如圖1所示。該接收系統的包括開環捕獲和閉環跟蹤2個部分。其中開環部分采用前導序列粗略估算出多普勒頻率和多普勒變化率，閉環部分采用三階PLL跟蹤剩余多普勒頻率和多普勒變化率并解調得到譯碼信息。

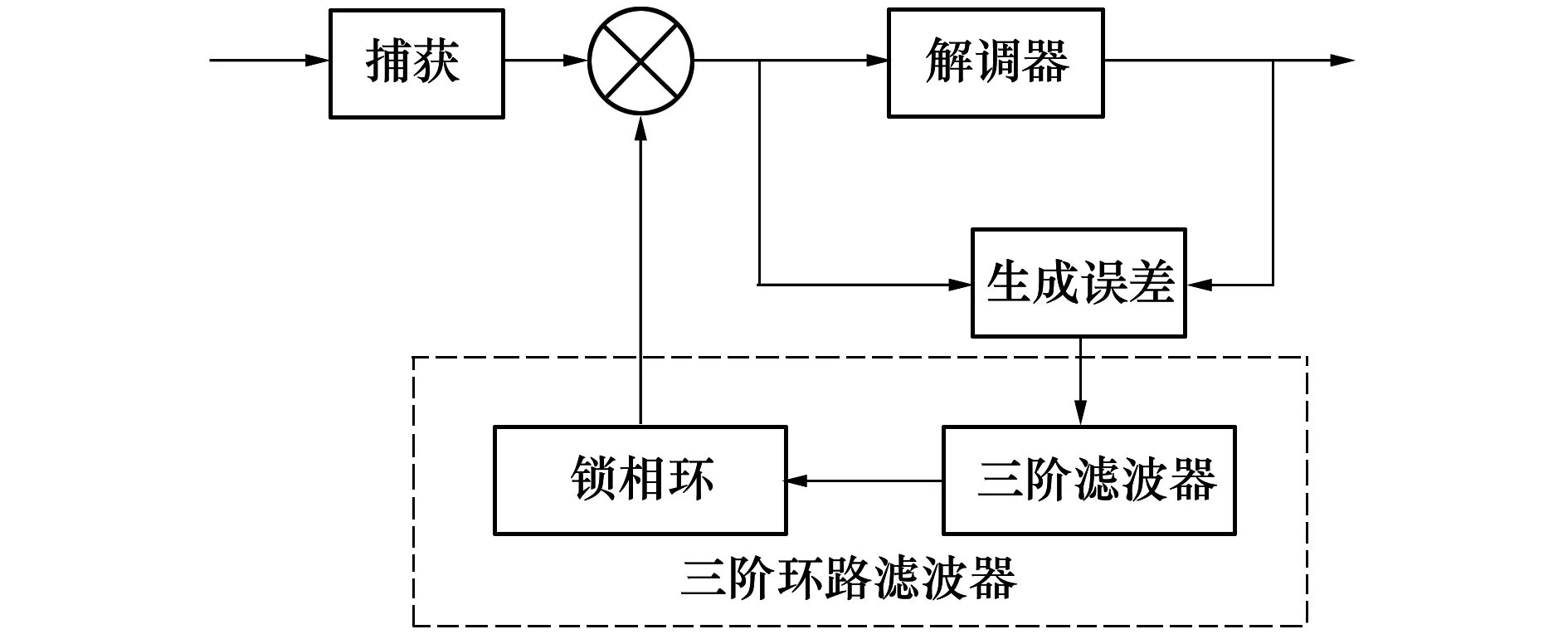
圖1 接收機載波同步系統框圖

2 開環捕獲

在捕獲操作中，利用了最小均方誤差(MMSE)方法獲得多普勒頻率偏移及其變化率偏移粗估計值。假設接收到的復基帶信號可以表示為：

r(t)=s(t)·ej(θ+Δft+0.5Δat2)+n(t)

(1)

式中，s(t)是已調信號,θ是載波的初始相位,Δf是多普勒頻率偏移,Δa是多普勒變化率偏移,n(t)表示高斯白噪聲,導頻長度為N,符號周期為T。Δf和Δa相應的對數似然函數為[6]

(2)

基帶信號相位為[7]

(3)

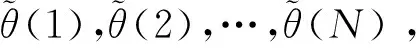
(4)

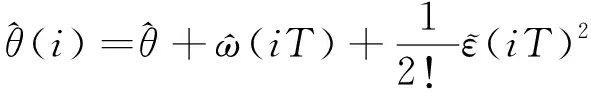
(5)

(6)

(-iT)

(7)

(8)

結合(6)～(8)式可以得到最終結果:

式中,計算系數αN,βN,γN分別表示如下

由于(9)式和(10)式推導出的多普勒頻率偏移和多普勒變化率偏移估計公式是閉式解形式,因此其復雜性是相當低的,能夠實現快速捕獲,適應高動態環境,快速得出多普勒頻率偏移和多普勒變化率偏移粗估計值。

3 閉環跟蹤

雖然經過開環捕獲后,剩余多普勒頻率偏移與變化率偏移已經控制在一個很小的范圍之內,但相位誤差仍會隨著時間推移而增加。由于三階環擁有跟蹤加速度的能力[8],因此可以用來跟蹤多普勒變化率。本文的閉環跟蹤三階環路濾波器的結構如圖2所示[9]。

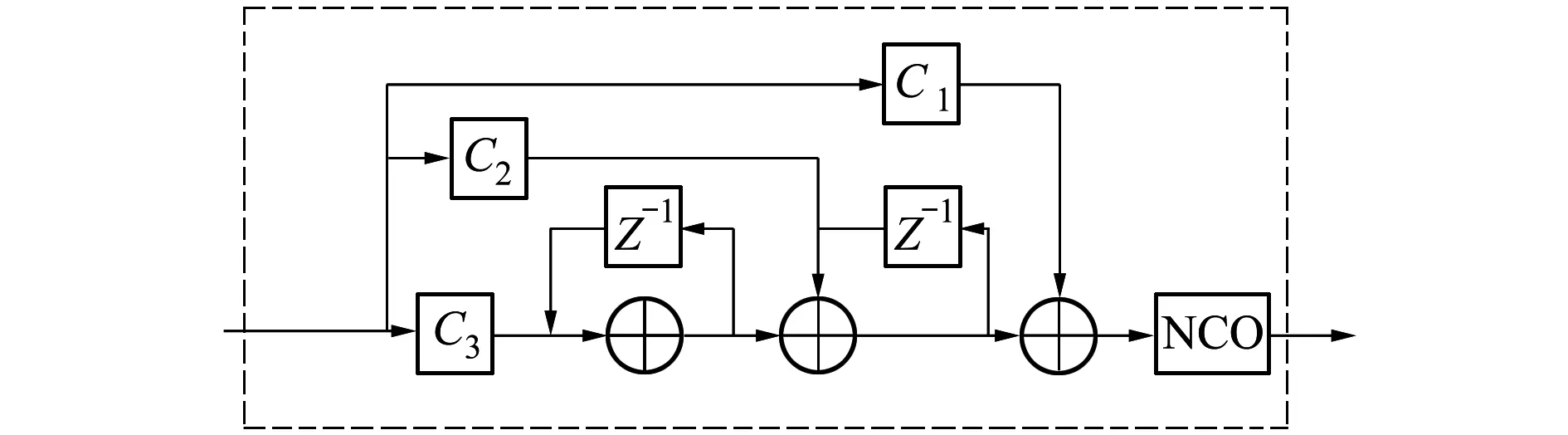
圖2 三階環路濾波器

其中,Z-1表示延時器,NCO表示數控振蕩器,C1,C2,C3表示濾波器參數,其值如下所示

(14)

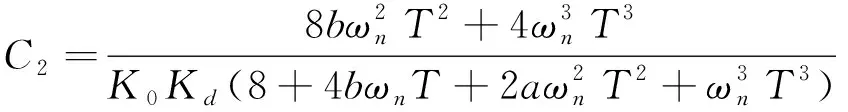
(15)

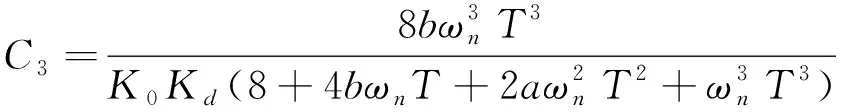
(16)

式中，Kd為鑒相器增益,K0為NCO增益,a=1.1,b=2.4為阻尼系數等于0.707的經驗值,ωn為環路固有頻率,與環路的等效噪聲帶寬的關系為

(17)

4 仿真分析

基于圖1所示的系統模型對本文提出的聯合開環捕獲閉環跟蹤算法進行仿真驗證。系統的各個仿真參數如下:采用QPSK調制,每幀1 000 bit數據,128 bit導頻,信噪比范圍設為(6 dB,12 dB),歸一化多普勒頻率偏移和多普勒變化率偏移范圍分別為(-0.25,0.25)和(-10-4,10-4)。為驗證本文提出的載波同步算法,分別對相位跟蹤曲線和誤碼率進行數值仿真。

在圖3中,當環路帶寬Bp=0.02時,約在700個數據符號之后該系統能穩定跟蹤參數。而當Bp=0.04時,達到穩定跟蹤需要約420個數據符號長度。當Bp=0.06時,該系統跟蹤載波信號僅需要300個數據符號。由該三階鎖相環的相位跟蹤曲線圖可以看出,三階鎖相環的環路帶寬Bp越高,系統進入跟蹤階段的速度越快。

圖4給出了,在歸一化多普勒變化率偏移ΔaT2=0.000 1,不同的環路帶寬Bp,以及不同的多普勒頻率偏移條件下,系統的誤碼率隨著信噪比變化的曲線,其中理論值為不存在多普勒頻率偏移和多普率變化率偏移的理想情況。從圖4a)可以看出,當Es/N0≥8 dB,Bp=0.04和Bp=0.02時,誤碼率曲線和理論值非常接近;同時環路帶寬越高,誤碼率越高。結合考慮圖2中的跟蹤時間和圖3中的誤碼率,我們認為選擇環路帶寬Bp=0.04更適合于進一步分析。由圖4b)可知,當Es/N0=8 dB,歸一化多普勒頻率偏移ΔfT=0.2時,誤碼率相比理論值僅損失1.1 dB。當歸一化多普勒頻率偏移ΔfT=0.15時,誤碼率相比理論值僅損失0.7 dB。

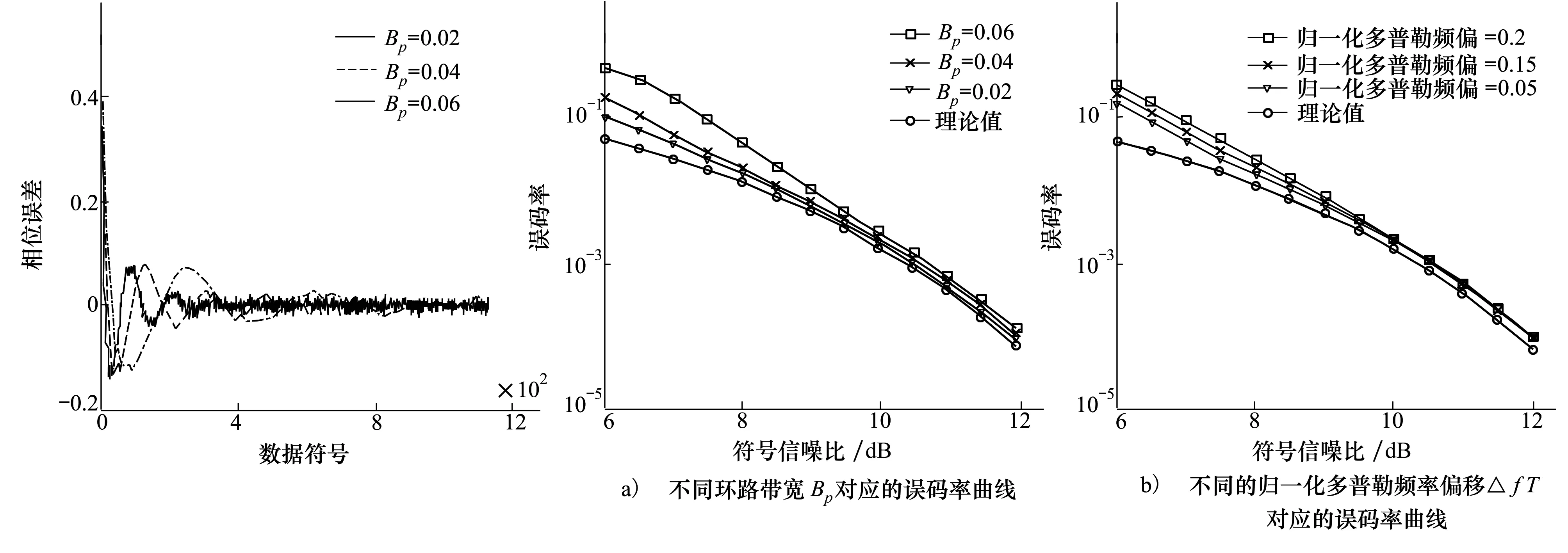
圖3 相位跟蹤曲線 圖4 誤碼率曲線

5 結 論

本文提出了在高動態環境下聯合開環捕獲和閉環跟蹤的載波同步算法。該算法將兩者結合并發揮兩者各自的優勢,從而可以實現快速捕獲和精確跟蹤。當信噪比為8 dB,歸一化多普勒頻率偏移ΔfT=0.15和歸一化多普勒變化率偏移ΔaT2=10-4時,誤碼率相比理論值僅損失0.7 dB。