某輸流管道兩種管壁應力作用下的屈曲分析

王文浩, 茍文選, 王富生, 劉偉, 岳珠峰

(1.太原科技大學 機械工程學院, 山西 太原 030024; 2.西北工業(yè)大學 力學與土木建筑學院, 陜西 西安 710129)

壓力管道在航空、航天、機械工程、工業(yè)與民用建筑以及其他眾多領域有著廣泛的應用。壓力管道在服役過程中會受到復雜載荷的作用，這些載荷主要包括管道正常工作狀態(tài)的外部壓力載荷、溫度載荷、管道及內部輸送介質自重、非工作狀態(tài)的安裝、檢修載荷以及地震載荷等。這些載荷都可能導致管道發(fā)生失穩(wěn)屈曲破壞[1]，因此對這些載荷進行詳細研究確定其對壓力管道屈曲性能的影響就顯得非常重要。對此中外眾多學者展開了廣泛的研究，如Lee等[2]分析了地震力作用下埋地管道的屈曲性能，但是其所采用動屈曲準分岔理論(quasi-bifurcation theory of dynamic buckling)較復雜，并不適合一般工程分析。Ji等[3]提出了管道塑性彎曲屈曲時名義應變的表達式，與試驗結果吻合較好，但公式較繁復，使用并不方便。Yudo和Yoshikawa[4]研究了缺陷L/D,D/t,δ0/t對純彎管道屈曲性能的影響。金瀏等[5]采用有限元軟件對地下管道進行了屈曲分析，采用線性特征值屈曲分析方法及考慮非線性影響的Riks法分別研究了管道的屈曲和后屈曲行為，但是并沒有考慮管道內部流體的影響。

對輸流管道應力作準確分析，一般都要涉及到流固耦合力學理論。而對于流固耦合問題的求解，通常采用有限元方法，需要耗時較長。對于有壓輸流管道，管道除了要承受垂直于管壁的壓應力外，由于液體的黏性，還將使管壁承受平行于管壁方向的切應力。對于同時承受壓應力、切應力和軸向壓力管道的屈曲和后屈曲承載力，目前研究較少。提出了某輸流管道在2種管壁應力作用下的屈曲分析方法，比流固耦合分析方法簡單而且效率高，更適合工程應用。

1 圓柱殼屈曲分析理論

管道本質上屬于兩端開口的圓柱殼。圓柱殼的屈曲理論主要是研究線彈性屈曲強度和非線性屈曲強度。

1.1 圓柱殼的線彈性屈曲強度

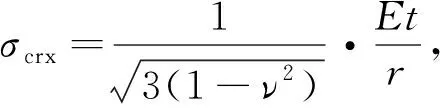
(1)

其適用范圍是

(2)

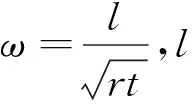
經過大量的試驗研究發(fā)現,圓柱殼的彈性屈曲應力,遠小于由(1)式計算出的彈性屈曲應力。原因是圓柱殼存在初始缺陷,越薄的圓柱殼這種差別越顯著,圖2表示完善的圓柱殼與非完善的圓柱殼屈曲后性能差別。需要應用非線性大撓度理論,對有初始缺陷的圓柱殼的軸壓屈曲性能展開研究,才可能得到實際的圓柱殼屈曲應力。

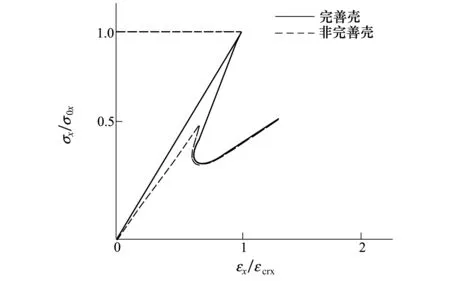
圖2 軸向受壓圓柱殼屈曲后性能

1.2 圓柱殼的非線性屈曲強度

在圓柱殼的加工、安裝和使用過程中,會產生徑向的位移或一定程度的損傷,可以認為是圓柱殼的初始缺陷,很多學者對含初始缺陷的圓柱殼穩(wěn)定性展開研究,但是目前尚沒有令人滿意的解法,工程上大多采用有限元方法,也可采用經驗公式估算。主要的經驗公式包括以下2種：

考慮初始缺陷的圓柱殼彈性狀態(tài)屈曲應力計算式

σ0x=0.33×0.605Et/r=0.4Et/d

(3)

考慮初始缺陷的圓柱殼彈塑性狀態(tài)屈曲應力計算式

σ0x=[1.64-0.23(d/t)1/4]fy≤0.4Et/d

(4)

(3)式、(4)式的適用范圍是:d/t≤100(235/fy)。fy為鋼材屈服強度設計值。

采用有限元法求解非線性屈曲臨界載荷時,需要將初始缺陷引入模型中,由于初始缺陷值取決于多種因素難以預先估計,本文采用的方法是以初始幾何缺陷來代替初始缺陷。施加初始幾何缺陷采用耦合缺陷模態(tài)法[7]。

本文采用有限元非線性分析,同時考慮了幾何非線性和材料非線性2個方面,均采用弧長法計算。為了簡化應力應變關系,同時盡可能準確地模擬管道的屈曲行為,本文采用應力應變簡化模式,如圖3所示。在圖中A點附近的領域為由比例極限至屈服極限的過渡段,采用光滑曲線過渡,避免應力突變。

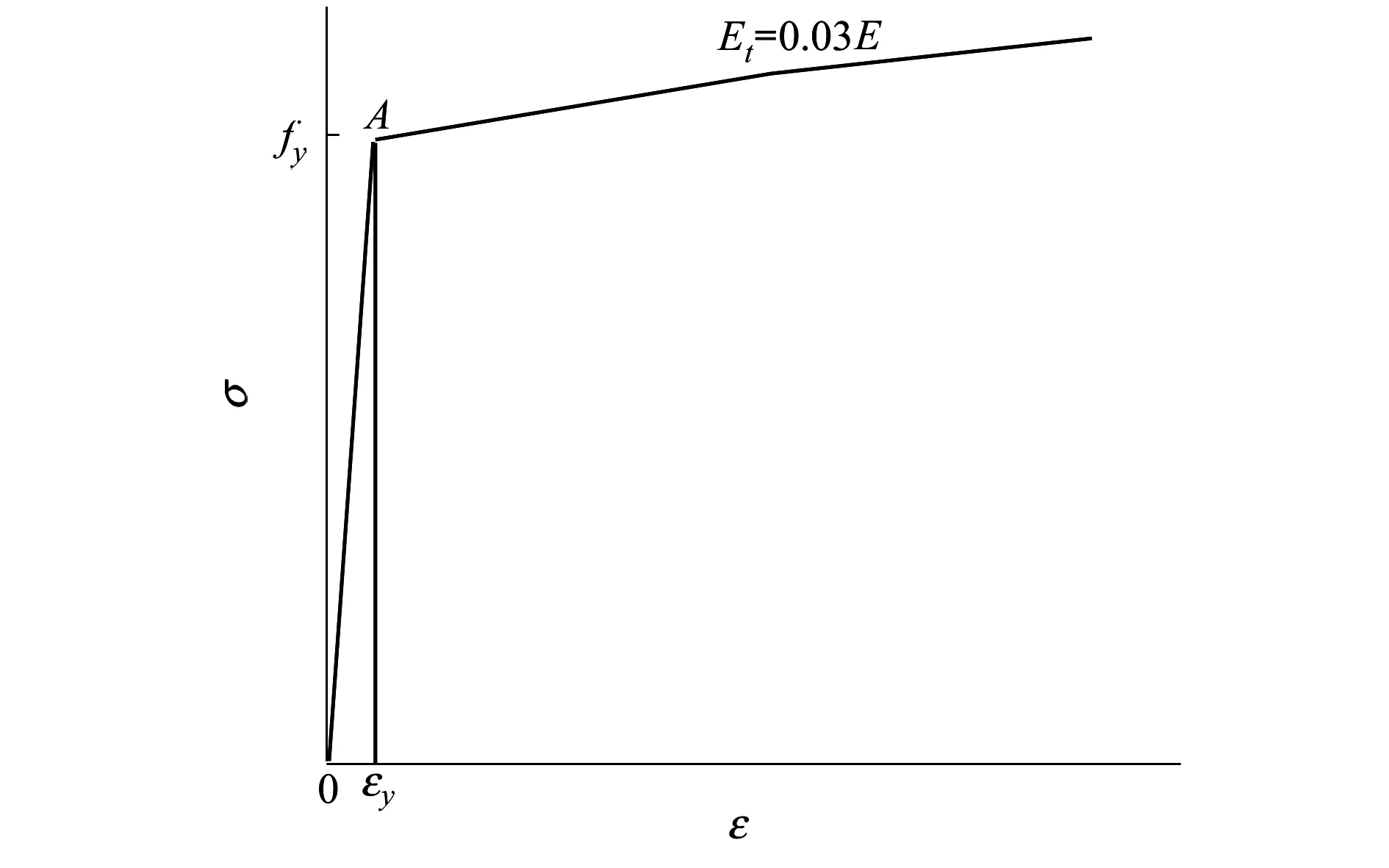
圖3 材料應力-應變曲線

1.3 2種圓柱殼內壁應力作用下的屈曲分析

本文針對2種圓柱殼內壁應力同時作用下的圓柱殼屈曲分析問題,建立的理論模型如圖4所示,采用有限元法進行分析。

2 輸流管道計算流程圖

圖5給出了輸流管道在2種管壁應力作用下處于工作狀態(tài)和非工作狀態(tài)時屈曲載荷的計算流程圖。從圖中可以看出非線性屈曲載荷的計算需要提取特征值屈曲分析的模態(tài)結果,工作狀態(tài)和非工作狀態(tài)計算結果分別采用了不同的驗證方法。在對模型進行簡化的基礎上,經過線性和非線性分析得出輸流管道的非線性屈曲載荷。

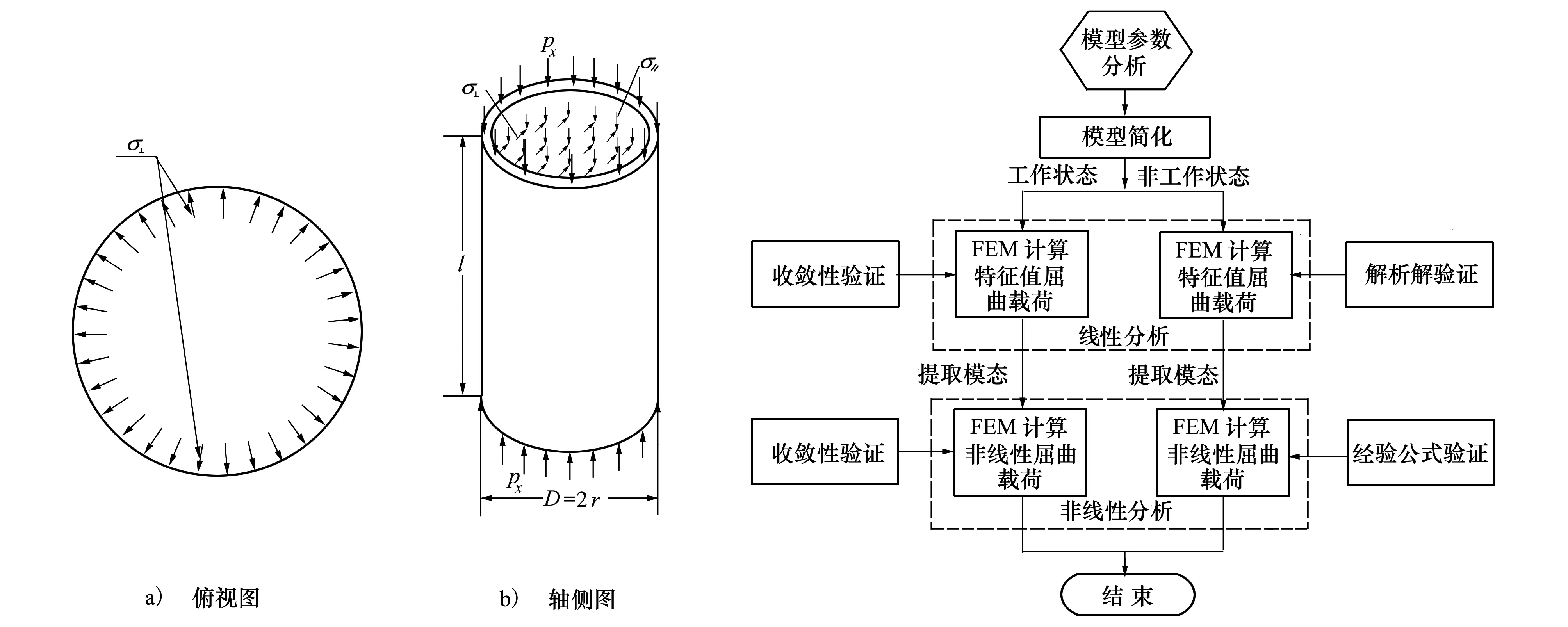
圖4 2種圓柱殼內壁應力作用下屈曲分析模型圖5 輸流管道屈曲載荷計算流程圖

3 輸流管道算例及模型簡化

3.1 輸流管道算例參數

所分析模型為某豎直敷設鋼輸水管道,其主要幾何尺寸及材料參數如表1所示,非工作狀態(tài)管道內沒有輸送介質,工作狀態(tài)管道內充滿水流,雙向流動且流速穩(wěn)定。

表1 管道幾何尺寸及材料參數

3.2 模型的簡化

由于管道流速穩(wěn)定,對水流引起的振動、沖擊力可以忽略不計,管道中均勻流動的液體對管壁的作用力可以分為壓應力和切應力。已知管道內均勻分布的壓應力為2 MPa,根據相關流體力學理論可計算出管壁切應力為:

根據文獻[8],同時考慮到實際工程中可能出現的各種情況(包括管道試壓時的最大應力),管道中出現的最大應力值可能達到設計應力值的1.5倍,因此

τo=1.5×0.66=0.99 MPa

此處取為1 MPa,同理對管道壓應力p,也增大到1.5倍,最大壓應力取3 MPa。這樣管道的壓應力波動范圍為0～3 MPa,切應力波動范圍為-1～1 MPa。

通過以上計算將管道內水流與管壁的流固耦合作用轉換為沿管壁作用的壓應力與切應力。下面分別對管道在非工作狀態(tài)下和工作狀態(tài)下的屈曲行為進行分析。

4 非工作狀態(tài)分析

在非工作狀態(tài)管道內沒有輸送介質,只有沿管道軸向的壓力作用。

4.1 特征值屈曲分析

本算例滿足公式(1)的適用條件(2),因此彈性屈曲應力值可以直接采用公式(1)進行計算,求得特征值屈曲壓應力為2 266 MPa。通過有限元方法計算,可得管道的一階屈曲模態(tài)如圖6所示,特征值臨界屈曲壓應力為2 162.7 MPa,與公式(1)算得的精確解比較誤差為4.8%,小于文獻[1]的誤差9%,本文有限元分析結果與經典解吻合較好。

圖6 非工作狀態(tài)一階屈曲模態(tài)

4.2 非線性屈曲分析

首先采用經驗公式進行計算,根據公式(4)及

鋼結構規(guī)范[9]的規(guī)定,可得

σ0x=207.1 MPa≤749.1 MPa

針對有限元分析,采用本文1.2節(jié)所述的非線性材料應力應變關系。由于本文模型前十階屈曲因子差別不大,本文取前十階模態(tài)的耦合結果,縮放系數取截面厚度的2%,采用Riks法計算。

非線性屈曲計算結果如圖7所示,從圖7a)中可以得出壓應力最大值為213.5 MPa,與(4)式的結果相比較相差3.1%,吻合較好,在達到最大值后承載力很快下降,之后的曲線呈現波浪式前進的特點,與文獻[10]中的變化趨勢一致。圖7b)顯示在管道的底部出現了折疊式失穩(wěn)模式,與文獻[10]試驗結果一致。由圖7c)可知在管道軸向壓力達到臨界屈曲載荷前,徑向位移基本呈線性變化,壓縮剛度基本保持不變,達到臨界屈曲載荷后承載力快速下降,徑向位移繼續(xù)增大一定值后,開始向反方向發(fā)展,可見管道在軸向壓力作用下首先產生軸向壓縮、徑向膨脹變形,當壓力達到臨界屈曲載荷后將逐漸向折疊式失穩(wěn)形式轉變,徑向產生相反的變形形式,這與文獻[10]中試驗觀察到的現象是一致的。

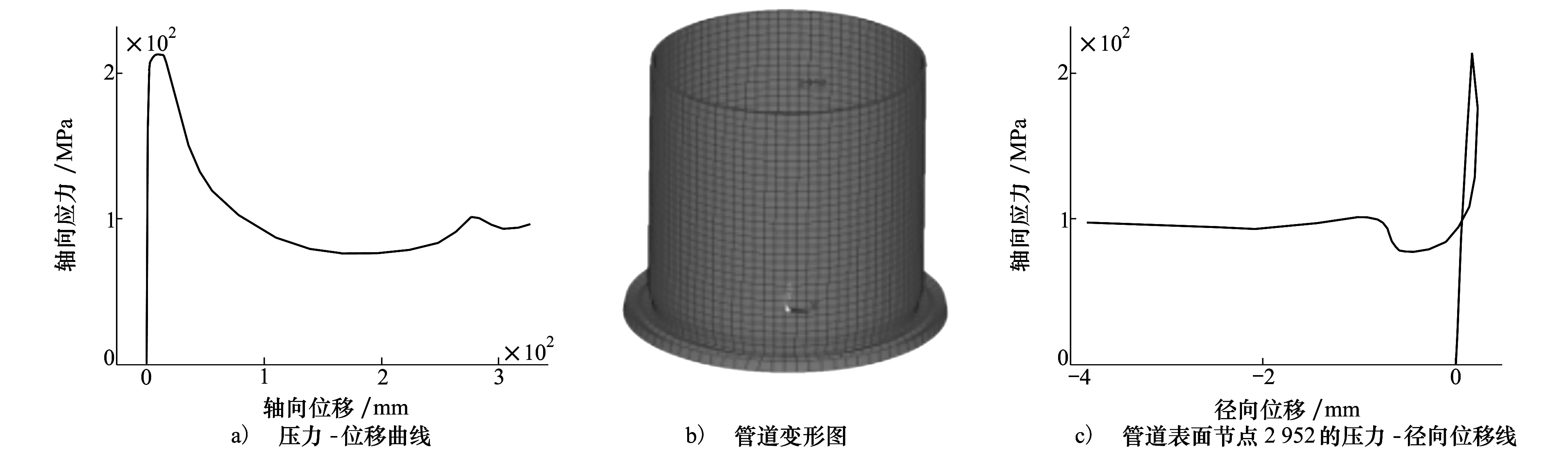
圖7 非工作狀態(tài)管道非線性分析

5 工作狀態(tài)分析

根據第3.2節(jié)的分析結果,管道在工作狀態(tài)時的受力情況可以簡化為內壁同時作用壓應力和切應力,下面將對簡化后的模型進行屈曲分析。

5.1 特征值屈曲分析

屈曲分析計算所得的特征值屈曲因子應乘以所有載荷的合力得到屈曲臨界載荷。本文壓力管道的特征值屈曲分析,是針對軸向載荷作用而言,而管壁作用的2種應力值屬于常數性質的載荷,應此需進行多次循環(huán)試算才能得到僅以軸向載荷為變量的屈曲臨界載荷值。

工作狀態(tài)特征值屈曲分析所施加的壓應力值分別為1 MPa，2 MPa，3 MPa,切應力值分別為1 MPa，0.5 MPa，0 MPa，-0.5 MPa，-1 MPa,對切應力規(guī)定與軸向壓力方向相同為正,反之為負。分別以這些應力作為常量計算軸向壓力作用下的臨界屈曲載荷。為驗證有限元計算結果的正確性本文進行了收斂性分析。以施加壓應力為1 MPa,切應力為1 MPa的計算模型為例,對模型分別劃分單元數為2 400,2 800,3 200,3 600,4 500,然后分別計算結果,以第5種劃分方法為精度最高,其余4種與之比較,計算出相對誤差列于表2中。從表中可以看出隨著單元數的增加相對誤差逐漸減小,到3 200個單元時相對誤差為1%,進一步加密單元,對計算精度提高不大,但是CPU計算時間卻大幅度增加,因此本文采取對計算模型劃分3 200個單元。

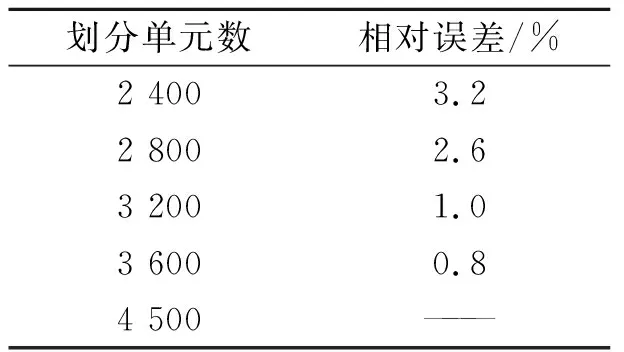
表2 工作狀態(tài)管道特征值屈曲載荷收斂性分析

本節(jié)計算結果如表3所示,從表中可以看出隨著切應力增大臨界載荷逐漸減小;而隨著壓應力增大臨界載荷逐漸增大。同時可以看出臨界屈曲載荷對切應力變化比壓應力變化更加敏感。各內壓下的屈曲模態(tài)近似,選擇壓應力為2 MPa,切應力為0.5 MPa的一階屈曲模態(tài)見圖8。

圖8 工作狀態(tài)一階屈曲模態(tài)(壓應力2 MPa,切應力0.5 MPa)

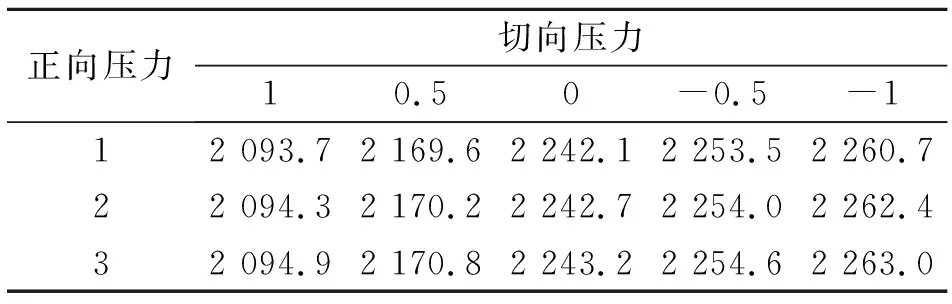
正向壓力切向壓力10.50-0.5-112 093.72 169.62 242.12 253.52 260.7 22 094.32 170.22 242.72 254.02 262.4 32 094.92 170.82 243.22 254.62 263.0

5.2 非線性屈曲分析

采用有限元方法對輸流管道進行工作狀態(tài)下的非線性屈曲分析,并對結果采用了與5.1節(jié)相同的收斂性分析,此處不再贅述。計算結果列于表4。從表4可以得出壓應力不變時,隨著切應力減小臨界屈曲載荷逐漸增大;在切應力不變時,隨著壓應力增大臨界屈曲載荷逐漸減小。同時從表中可以看出非線性屈曲載荷對切應力比壓應力更加敏感。

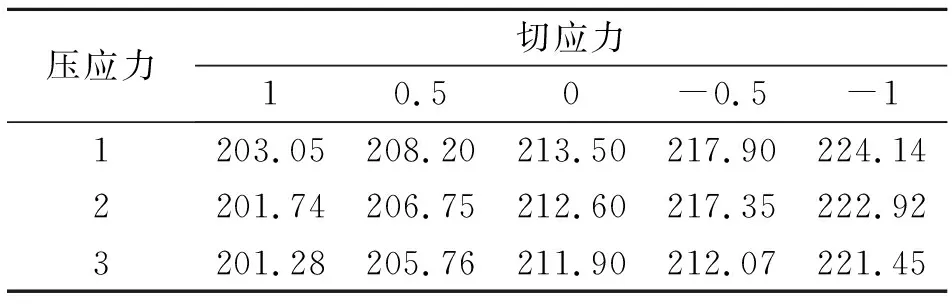
表4 管道在2種內壓下的非線性屈曲臨界載荷 MPa

在工作狀態(tài)各種應力作用下管道的軸向壓力位移曲線與變形圖差別不大,這里選擇壓應力為1 MPa,切應力為1 MPa的內力作用下管道的非線性屈曲分析結果如圖9所示。其中圖9a)與圖9c)顯示屈曲臨界載荷為203.05 MPa。圖9中a)～c)與圖7中a)～c)相似,說明2種狀態(tài)下變形形態(tài)是很相似的。

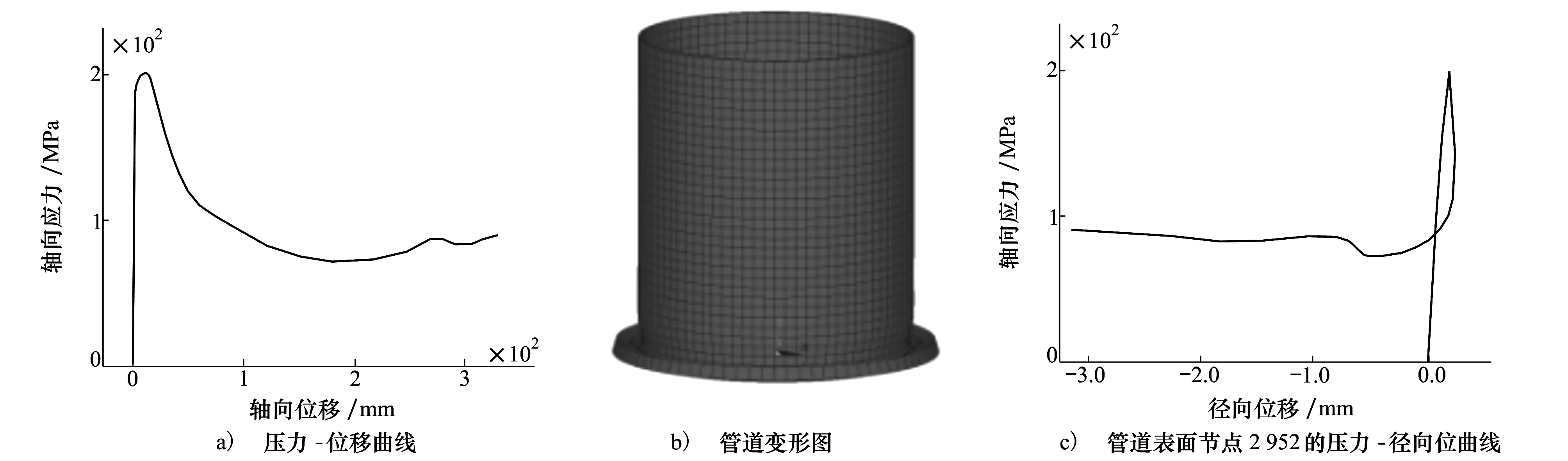
圖9 工作狀態(tài)管道非線性分析(壓應力1 MPa,切應力1 MPa)

比較表3、表4可以得出,壓應力不變,隨著切應力的減小特征值屈曲臨界載荷與非線性屈曲臨界載荷均增大,這是由于隨著切向壓力的減小可以減小總軸向壓力的作用;切應力不變,隨著壓應力的增大特征值屈曲臨界載荷增大,非線性屈曲臨界載荷減小,這是由于特征值屈曲分析將材料視為線彈性材料,其剛度值不變,而非線性屈曲分析考慮了材料的非線性,材料達到比例極限后剛度值隨著載荷的增大發(fā)生折減。

5.3 流固耦合方法與本文方法效率比較

采用ANSYS軟件對工作狀態(tài)下的輸流管道進行流固耦合分析[11],計算出其特征值屈曲臨界載荷和非線性屈曲臨界載荷。將分析結果與本文方法所得結果在CPU計算時間方面進行了比較。以正向壓力2 MPa,切向壓力0.5 MPa為例,如表5所示。從表中可以看出本文方法比流固耦合方法在CPU計算時間上縮短了很多,計算效率明顯提高。

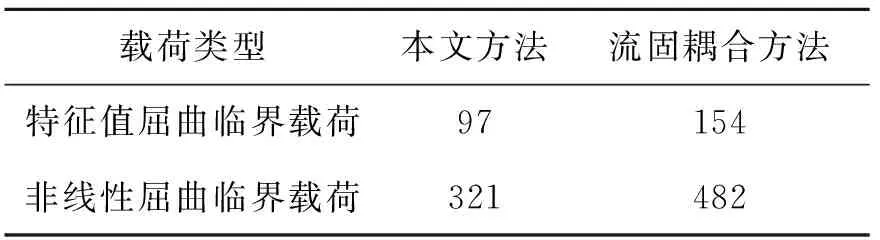
表5 本文方法與流固耦合方法計算效率比較 s

6 討 論

通過以上分析可知，工作狀態(tài)與非工作狀態(tài)下非線性屈曲變形是非常相似的，沒有受到2種應力作用的影響，如圖7與圖9所示。文獻[6]指出，圓柱殼的屈曲模態(tài)主要有網格式和軸對稱式2種形式，在本文中圖6為網格式,圖8為軸對稱式，而這2種形式本質上也是相同的[12]。

通過分析結果可知，管道的特征值臨界屈曲載荷高達2 000 MPa以上，顯然與實際情況不符，原因是這一結果是在線彈性小變形假設下得出的，當本文考慮了幾何缺陷和2個非線性因素的影響后，采用非線性屈曲分析所得的屈曲臨界載荷則與實際情況較為接近。可見對于管道這樣對缺陷十分敏感的結構，其實際承載力通常取決于非線性分析的結果。

7 結 論

本文對軸壓載荷作用下輸流管道的屈曲性能進行了分析，得出以下結論。

1) 采用沿管壁的壓應力和切應力代替水流對管道的作用力，可以簡化計算，即將較復雜的流固耦合力學問題轉化為單純的固體力學問題，提高了計算效率。

2) 工作狀態(tài)和非工作狀態(tài)管道的特征值屈曲模態(tài)、非線性屈曲變形相似。

3) 特征值屈曲計算的結果與考慮缺陷的非線性屈曲計算值差別很大，不能作為工程設計依據，但是其變形模態(tài)對非線性分析有一定的影響。

4) 工作狀態(tài)的壓力管道，切應力不變，隨著壓應力增大特征值屈曲臨界載荷增大，而非線性屈曲臨界載荷減小。壓應力不變，切應力與軸向壓力方向相同時，隨著切應力絕對值增大，屈曲臨界載荷減小；壓應力不變，切應力與軸向壓力方向相反時，隨著切應力絕對值增大，屈曲臨界載荷增大。

5) 壓力管道的屈曲載荷對切應力比壓應力更加敏感。