電磁彈性材料Ⅲ型界面斷裂分析

周震寰, 徐旺, 鄧子辰, 徐新生, 徐成輝

(1.大連理工大學 工程力學系 工業裝備結構分析國家重點實驗室, 遼寧 大連 116024;2.西北工業大學 力學與土木建筑學院, 陜西 西安 710072)

隨著材料科學的發展,具有多物理場耦合特性的電磁彈性復合材料已經廣泛用于智能器件的開發與制造中[1-2]。該類材料往往由兩相或多相壓電和壓磁材料按照一定的方式復合而成。由于不同材料相間的失配性,電磁彈性復合材料在制造和使用過程中會不可避免地出現界面裂紋。這些裂紋會在外荷載作用下產生應力集中,進而引發結構失效破壞,造成安全事故。因此,研究電磁彈性復合材料的界面斷裂問題具有重要的理論和實際意義。

在現有研究中,解析方法往往僅限于求解無限大或半無限大電磁彈性材料中的裂紋問題,如積分方程方法[3]、Stroh變換方法[4]。對于有限幾何尺寸的含裂紋電磁彈性材料還主要依賴于數值方法,如有限元方法[5]、邊界元法[6]和無網格方法[7]。然而,大部分數值方法僅適用于單相電磁彈性材料,無法直接應用于雙相電磁彈性復合材料的界面斷裂分析。為解決上述問題,本文提出一種適用于電磁彈性復合材料反平面界面斷裂分析的辛離散有限元方法。該方法將一類基于哈密頓體系的解析方法[8]與傳統有限元方法相結合,能夠簡單、高效地獲得相關斷裂參數,并同時獲得裂紋尖端附近奇異物理場的顯式表達式。目前,該方法已經成功應用于彈性材料與壓電材料的斷裂分析中[9]。

本文提出的辛離散有限元方法可以分為2步：第一,根據裂紋尖端的位置將整體結構分為2類區域,即包含奇異性的近場和無奇異性的遠場；第二,通過在裂紋尖端附近引入解析的辛本征解函數,實現該區域內的未知量變換,將數量龐大的節點未知量轉化為少量的辛本征解待定系數。該方法可以避免傳統有限元方法在計算斷裂參數時的網格敏感性和路徑依賴性,直接提高計算效率和計算精度。

1 電磁彈性材料反平面有限元列式

考慮如圖1所示的含界面裂紋的電磁彈性復合材料。上下層材料分別記為材料1(M1)和材料2(M2),z軸選取為電磁彈性介質的極化方向,坐標原點位于裂紋尖端。結構承受反平面剪應力τ0,平面內電位移D0和磁感應強度B0。曲線Γ0將整體結構劃分為2類區域,即近場區域和遠場區域。

在直角坐標系下,電磁彈性復合材料在反平面荷載作用下的基本方程可以表示為:

本構方程

(1)

幾何方程

(2)

平衡方程

(3)

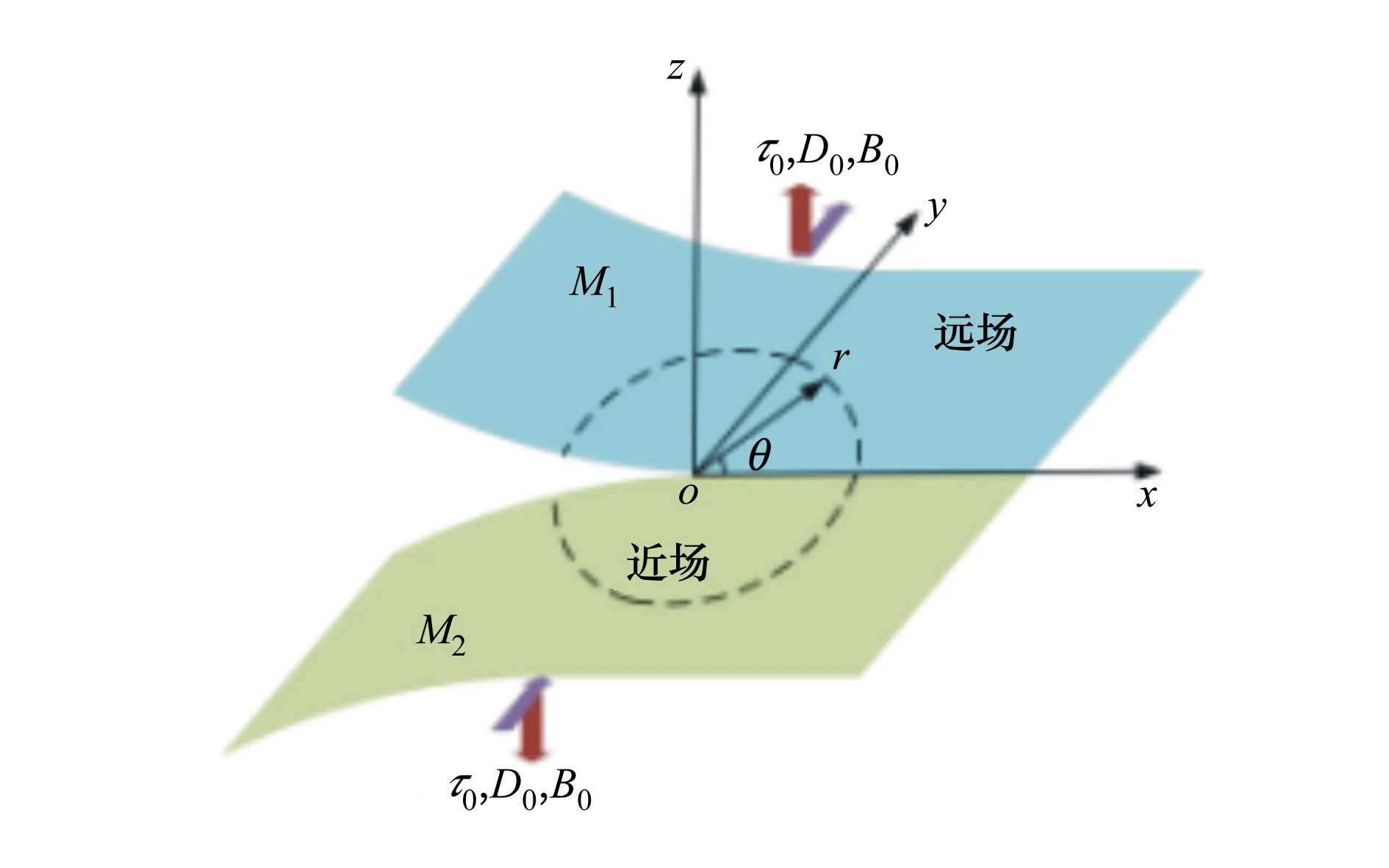
圖1 含裂紋電磁彈性復合結構

本文使用的電磁彈性材料單元為八節點四邊形單元。單元內任意點未知量由節點未知量表示

(4)

式中，Nj是形函數。單元勢能可以表示為

(5)

式中，L(i)為應變能密度函數

(6)

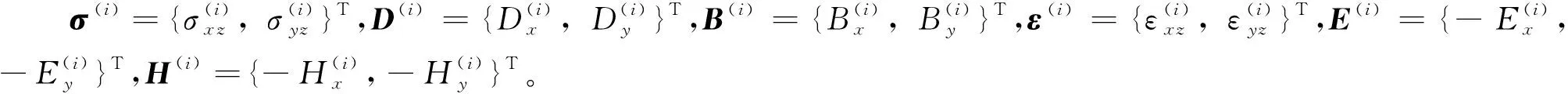
將(1)式、(2)式和(4)式帶入(5)式可得

(7)

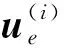
根據最小勢能原理δΠ(i)=0,可得

(8)

式中，Ke是單元剛度矩陣。根據節點編號,組集整體剛度矩陣、節點位移向量和整體載荷向量,可得電磁反平面有限元列式為

(9)

式中，K為剛度矩陣,f為荷載向量,下標N和F分別代表近場和遠場區域。

2 電磁彈性材料Ⅲ型界面斷裂辛方法

在近場區域,定義全狀態向量為

Ψ(i)={q(i),p(i)}T=

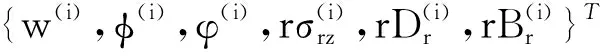
(10)

則電磁彈性復合材料Ⅲ型界面斷裂問題的哈密頓控制方程可以表示為

(11)

式中，H(i)為哈密頓矩陣,見附錄(A-2)。界面連續條件為

q(1)|θ=0=q(2)|θ=0,R(1)gq(1)|θ=0=R(2)gq(2)|θ=0

(12)

裂紋面邊界條件為

R(1)gq(1)|θ=π=0,R(2)gq(2)|θ=-π=0

(13)

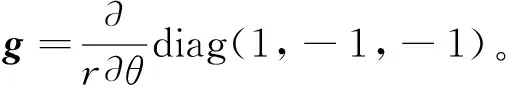
利用分離變量法求解哈密頓方程(11),并結合(12)式和(13)式得到問題的辛本征值和本征解,見附錄(A-3～A-7)。因此,雙材料電磁反平面的位移,電勢和磁勢可以表示為

(14)

式中，M是所取的本征解項數,cj, k為待定系數。

3 辛離散有限元方法

由(14)式,近場區域內節點未知量可以表示為

uN=Φc

(15)

式中，c={c0, 1,c0, 2,c0, 3,c1, 1, …,c1, 6,c2, 1, …,cM, 6}T為辛展開函數的待定系數向量

(m=1, 2, …,NΩN;j=1, 2,…, 3M+6),NΩN為近場區域內總節點數,(rm,θm)是第m個節點的極坐標。將(15)式代入(9)式,則電磁反平面斷裂問題的辛離散有限元表達式為

(16)

4 強度因子和能量釋放率

由(1)式和辛本征解可知,在裂紋尖端(r=0)[10],廣義應力強度因子可以表示為

(17)

式中,K3,KD和KB分別為應力強度因子、電位移強度因子和磁感應強度因子,是由反平面剪應力τ0,平面內電位移D0和磁感應強度B0耦合作用的結果。能量釋放率為

(18)

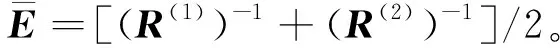
5 數值算例

為驗證本文提出方法的正確性與有效性,數值算例計算了3種典型裂紋對應的斷裂參數。本節中所有計算數據均采用無量綱形式[10],涉及的材料參數如表1所示。

表1 材料參數

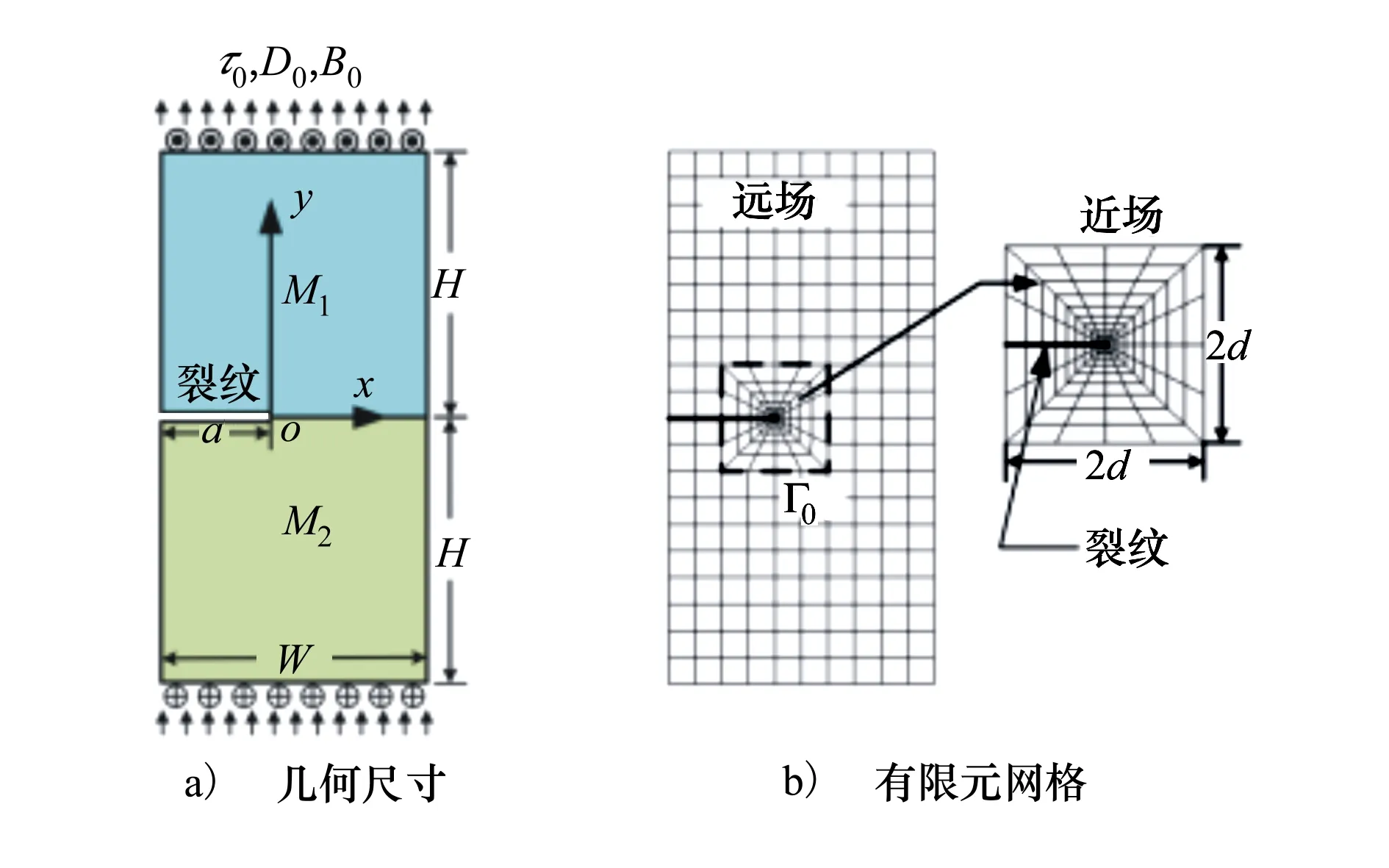
圖2 含邊裂紋電磁彈性矩陣板

5.1 算例1

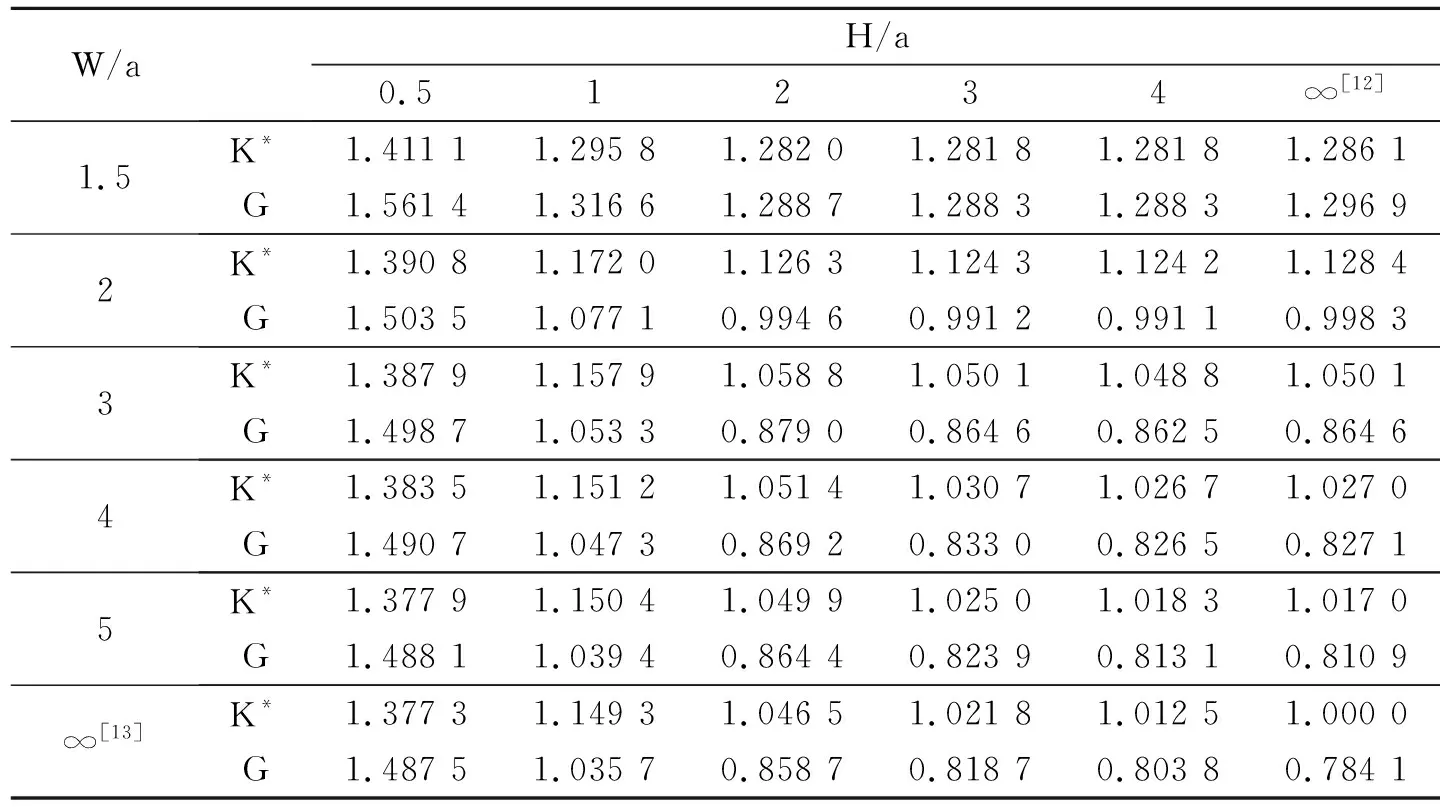
表2 不同高度和寬度對應的強度因子和能量釋放率

5.2 算例2

圖3為1個含有平行裂紋的電磁彈性材料矩形板,其裂紋長度分別為2a1和2a2。該板兩端受到均布荷載τ0=1,D0=1和B0=1作用。令W=1,H/W=0.5,H1/W=0.5,表3給出了不同裂紋長度對應的裂紋尖端A處的強度因子與能量釋放率。從表中數據可以看出,對于給定的a2,各強度因子與能量釋放率總是隨著的a1增加而增大;而對于給定的a1,斷裂參數表現出相反的變化趨勢。表4給出了裂紋長度相同時(a1=a2)斷裂參數隨H/W的變化規律。從表中可以看到,各斷裂參數隨著H/W單調變化,并逐漸趨近于某一固定值。該現象可以通過圣

維南原理解釋,當H/W增加到一定值時,邊緣效應不再對裂紋尖端物理場分布產生影響。

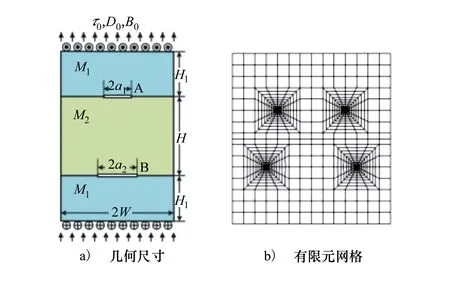
圖3 含2條平行裂紋電磁矩陣板

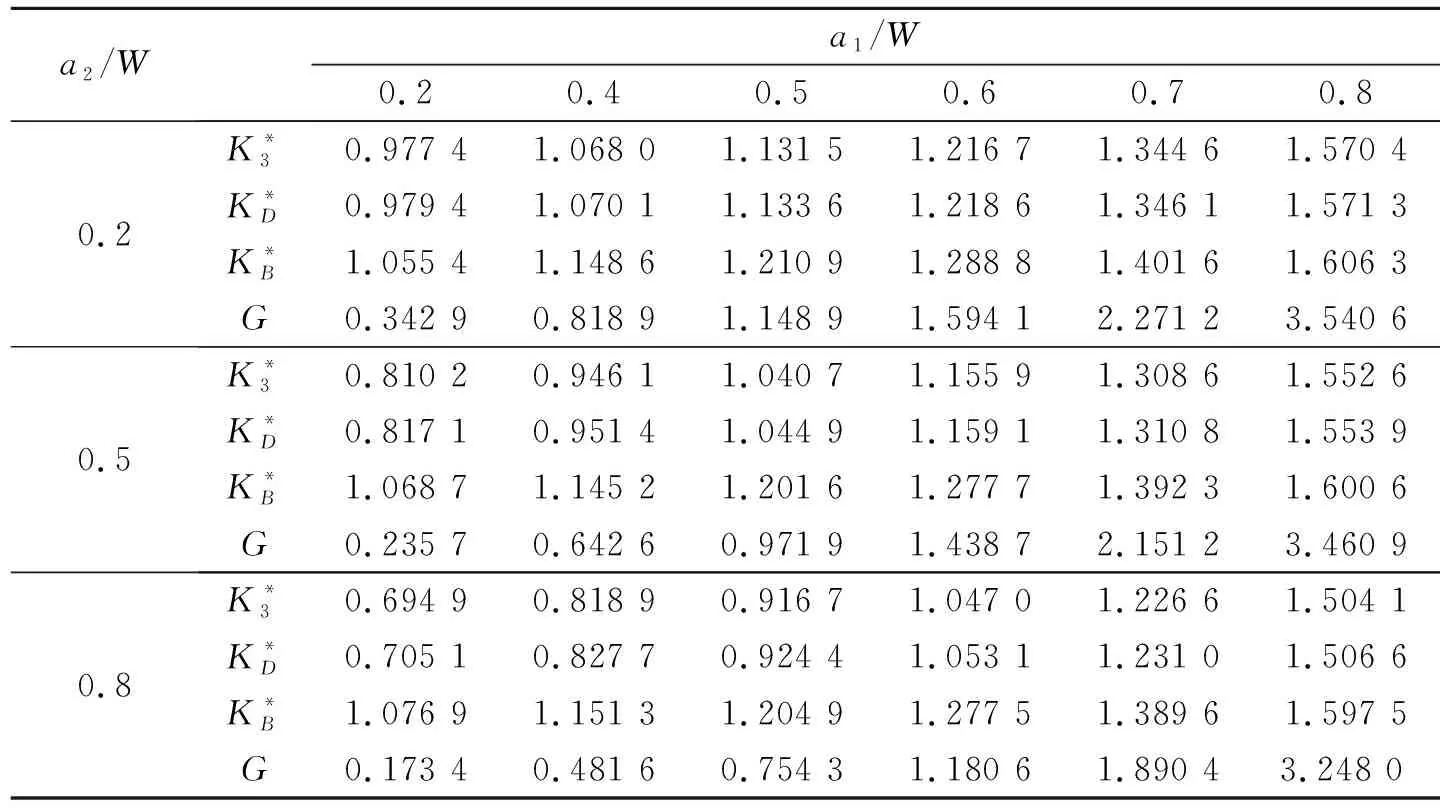
a2/Wa1/W0.20.40.50.60.70.80.2K*30.977 41.068 01.131 51.216 71.344 61.570 4K*D0.979 41.070 11.133 61.218 61.346 11.571 3K*B1.055 41.148 61.210 91.288 81.401 61.606 3G0.342 90.818 91.148 91.594 12.271 23.540 60.5K*30.810 20.946 11.040 71.155 91.308 61.552 6K*D0.817 10.951 41.044 91.159 11.310 81.553 9K*B1.068 71.145 21.201 61.277 71.392 31.600 6G0.235 70.642 60.971 91.438 72.151 23.460 90.8K*30.694 90.818 90.916 71.047 01.226 61.504 1K*D0.705 10.827 70.924 41.053 11.231 01.506 6K*B1.076 91.151 31.204 91.277 51.389 61.597 5G0.173 40.481 60.754 31.180 61.890 43.248 0

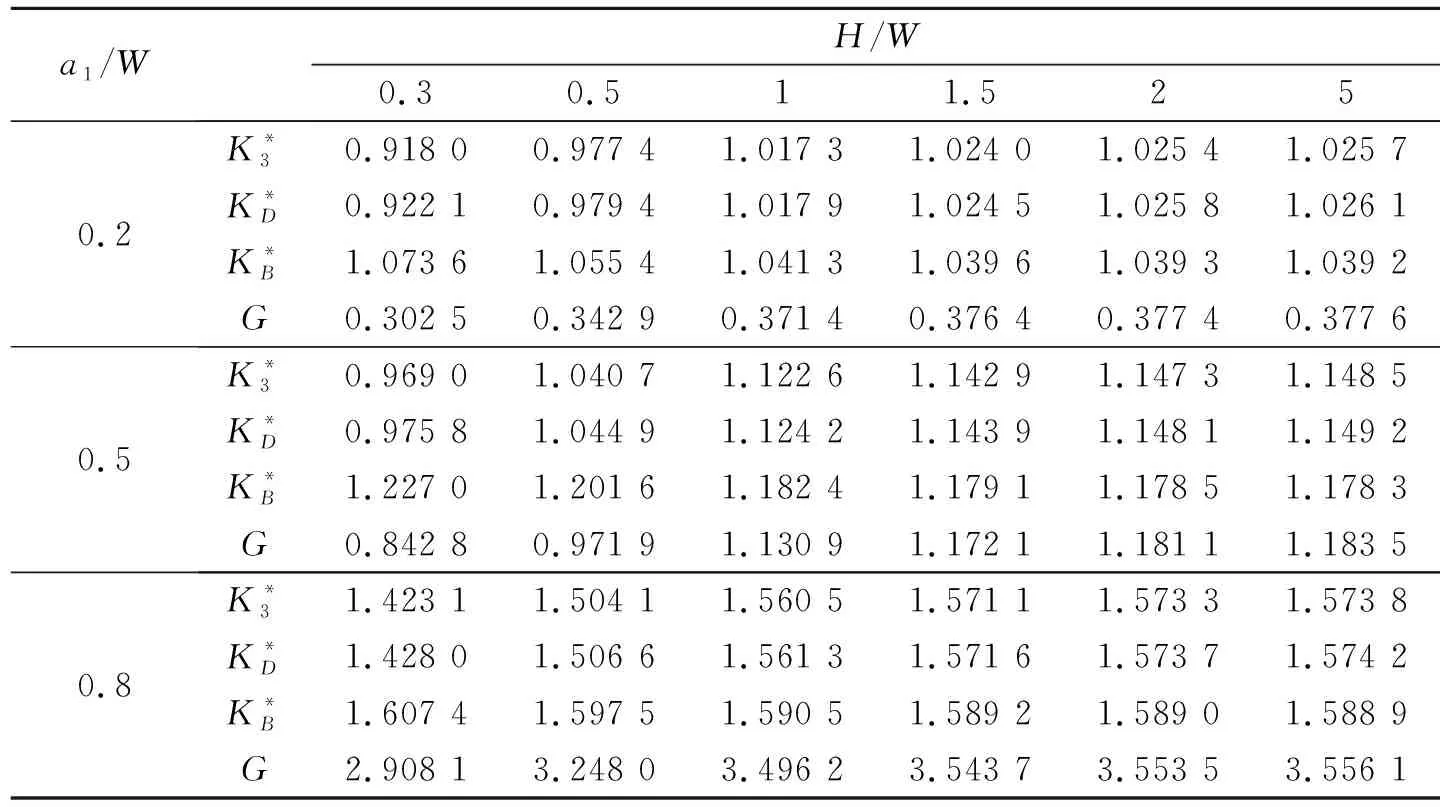
表4 裂紋尖端A的強度因子和能量釋放率(a1=a2)

5.3 算例3

考慮如圖4所示的1個含有折線裂紋的電磁彈性材料矩形板。裂紋與水平方向的偏離角度分別為θA和θB。令W=H,a=0.4H,τ0=1,D0=1和B0=1,表5和表6分別給出了的裂紋尖端A和B處的強度因子和能量釋放率隨θA和θB的變化規律。從表5中可以看出,所有斷裂參數隨θA的增大均表現出先增大后減小的趨勢。當θA=0時,應力、電位移強度因子和能量釋放率達到最大值。表6表現出與表5相似的變化趨勢。從上述現象可以看出,合理控制外部電磁場可以有效改變電磁彈性材料裂紋尖端的能量釋放率,從而阻滯裂紋擴展。

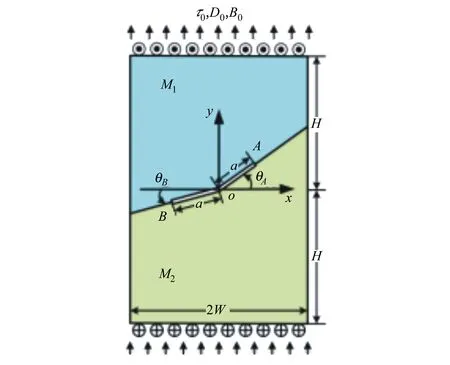
圖4 含有折線裂紋電磁矩形板

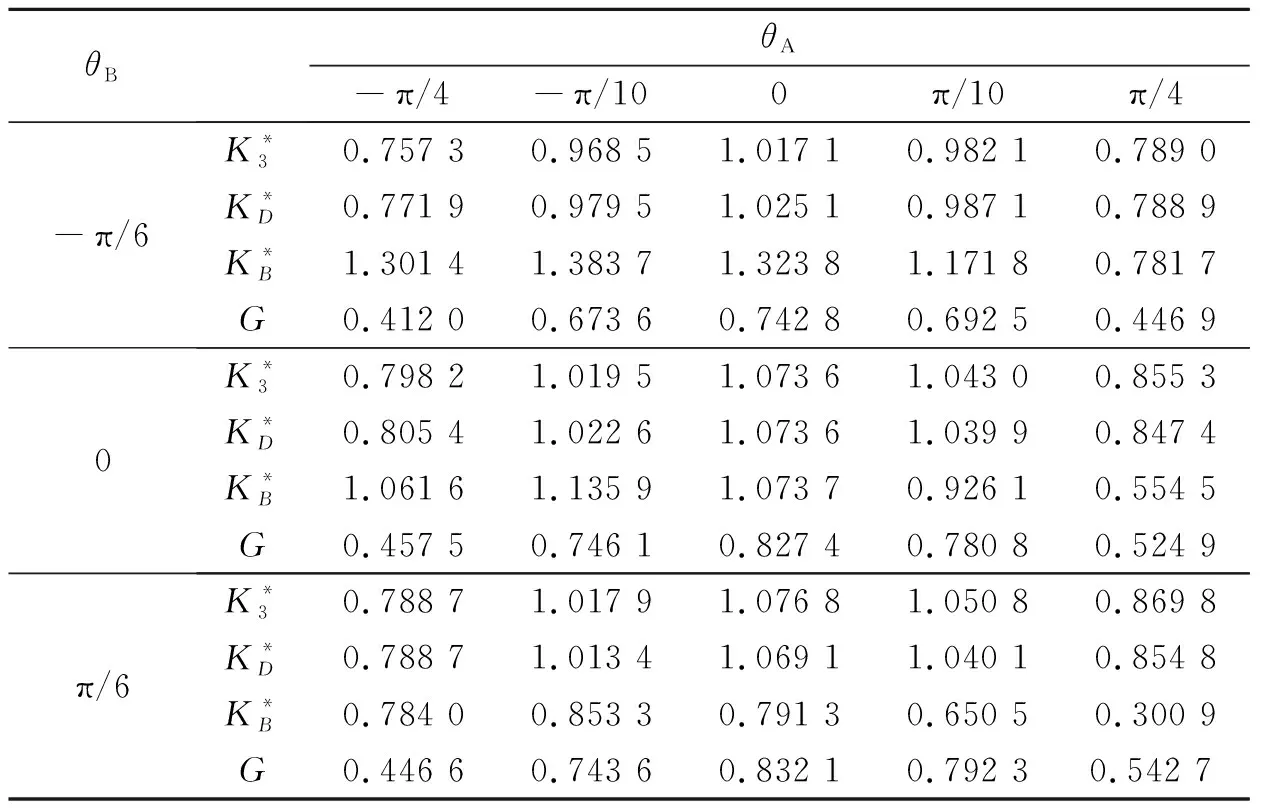
θBθA-π/4-π/100π/10π/4-π/6K*30.757 30.968 51.017 10.982 10.789 0K*D0.771 90.979 51.025 10.987 10.788 9K*B1.301 41.383 71.323 81.171 80.781 7G0.412 00.673 60.742 80.692 50.446 90K*30.798 21.019 51.073 61.043 00.855 3K*D0.805 41.022 61.073 61.039 90.847 4K*B1.061 61.135 91.073 70.926 10.554 5G0.457 50.746 10.827 40.780 80.524 9π/6K*30.788 71.017 91.076 81.050 80.869 8K*D0.788 71.013 41.069 11.040 10.854 8K*B0.784 00.853 30.791 30.650 50.300 9G0.446 60.743 60.832 10.792 30.542 7

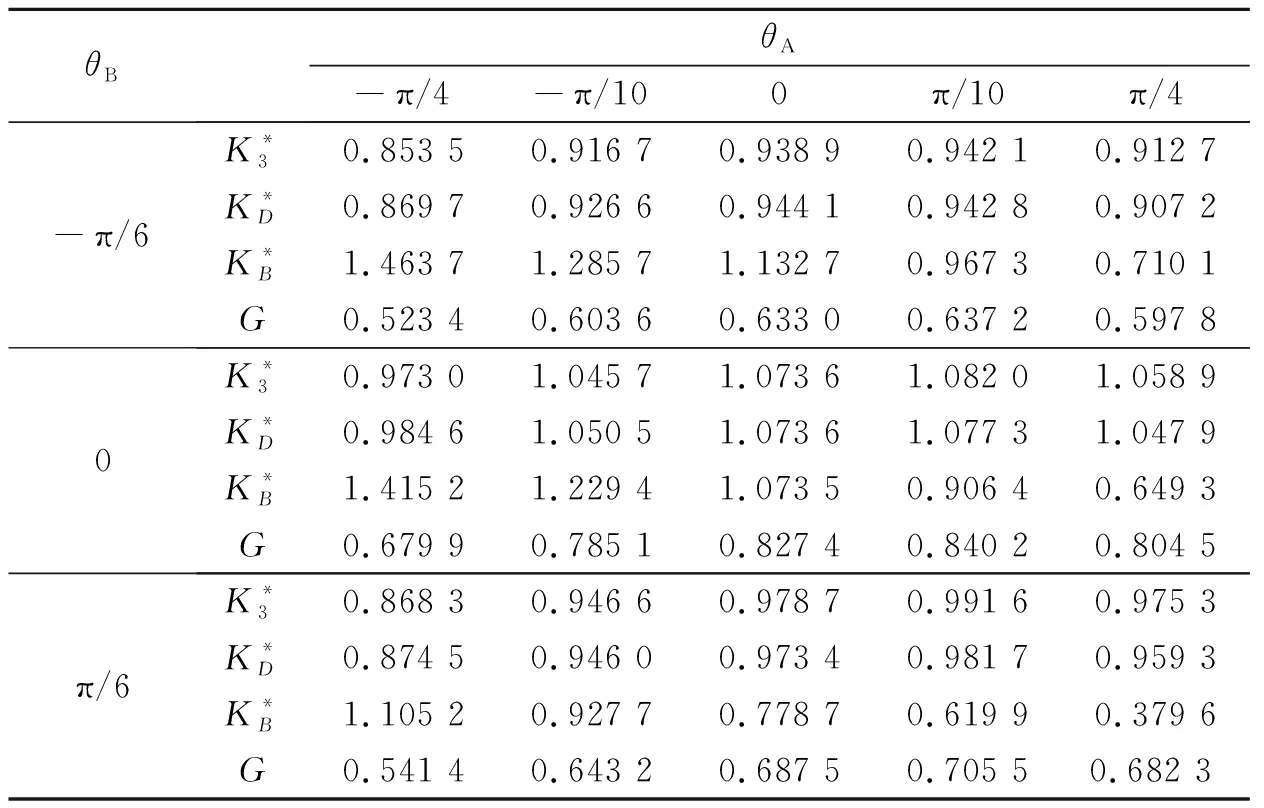
表6 裂紋尖端B強度因子和能量釋放率隨θA的變化

6 結 論

本文將辛離散有限元方法成功應用于電磁彈性復合材料在反平面荷載作用下的界面斷裂分析中。該方法將傳統有限元方法與哈密頓體系辛方法有機結合,可以直接計算出高精度的應力、電場、磁場強度因子和能量釋放率,并同時獲得裂紋尖端附近區域各物理場的顯式表達式。相比其他數值方法,該方法有三方面優勢:①在裂紋尖端奇異區域內引入具有辛展開形式的解析解,將該區域內傳統有限元對應的大量節點未知量轉化為少量辛本征解待定系數,解決了傳統有限元方法中斷裂分析的網格敏感性問題,并同時大幅提高了計算效率;②引入的辛本征解函數能夠直接表征裂紋尖端的奇異性,避免了傳統有限元方法中斷裂參數計算的路徑依賴性問題,直接提高了應力強度因子計算精度;③無需額外引進新的單元以及后處理程序,可以直接獲得裂紋尖端附近奇異物理場的顯式表達式,有利于該類結構的前期優化設計與后期安全評估。

附錄A

(A-1)

(A-2)

式中

(A-3)

(A-4)

(A-5)

(A-6)

(A-7)

式中，φj=rμjsin(μjθ),φj=rμjcos(μjθ);μj=j/2是辛本征值;ρ=(R(2))-1R(1),n=1, 2, 3, …。