把握教學“四點”，知識能力并重

袁媛

[摘? 要] 三角形的內角和是三角形的重要性質，其對幾何內容的學習極為重要. “三角形的內角和”的課堂教學需要處理好起點、生成點、發展點和提升點四個關鍵點，文章將結合新課標理念對其加以探究，提出相應的教學建議.

[關鍵詞] 三角形內角和;理性認知;探究;證明;例題

“三角形的內角和”是蘇教版七年級下冊的重要教學內容，該內容探討的是三角形的一個重要性質，對三角形內角之間的關系有著深刻的揭示，也是后續多邊形內角、三角形外角性質和相關角度計算與證明的基礎，因此屬于基礎性極強的內容，下面對其展開教學探討.

以學生的認知基礎作為教學的

起點

教學的起點設定關系到整個教學過程的成功與否，因此應該慎重選取教學起點，幫助學生順利完成課堂過渡. 一般教師應該以學生的認知水平和已有知識經驗作為教學的基礎，采用“溫故知新”的方式開展課堂引入教學.

學生在小學階段通過直觀感受已經了解到三角形的內角和為180°，而初中階段學習的關鍵是幫助學生完成感性認識到理性認知的過渡，因此使學生掌握演繹推理的思路和方法才是教學的重點. 教師在教學伊始就需要理清幾個重要的問題，然后基于問題來設計教學，即學生已經掌握的知識，本節課的教學重點，如何引導學生遞進思考.

而在實際教學中可以采用設問的方式引導學生進行思考，從而聯系舊知探索新知，可設置如下問題串.

[圖1]

問題1：圖1所示是一個一般的三角形，大家知道它的內角和是多少度嗎？

問題2：大家是如何知道的，可以采用哪些方法說明？

問題3：大家小組討論，是否有更為直觀的方式來證明？

在設問引入階段需要給學生充分的時間，讓學生獨立思考，交流探討，充分調動知識經驗來探索三角形內角和，激發學生的學習興趣，使課堂教學向著積極有利的方向發展.

以多樣的探究活動作為教學的

生成點

“三角形的內角和”教學的難點和重點是性質定理的論證過程，該過程中所滲透的方法和思路對于整個幾何內容的教學有著重要的啟示作用. 一般對于幾何性質定理的教學采用探究式的教學方式，一般探究的過程中需要借助多樣的探究活動，讓學生通過體驗探究的過程來完成知識生成，這也是教學的生成點.

對于三角形的內角和的探究論證，一般采用拼圖的方式，該方式的優勢在于直觀簡潔，容易操作，因此在教學中可以設計多樣的拼圖活動，使學生充分參與，自我感知. 例如可以設置如下拼圖活動：請大家準備一個三角形紙板，將三角形的三個內角撕下來，嘗試采用拼圖的方式來證明三角形的內角和等于180°. 拼圖的過程學生在小學階段已經體驗過，而中學教學中需要使學生關注幾個問題點：①學生拼合的方式可能略有不同，拼圖的總體思路是什么？（使三個內角拼接在同一點上，形成一條直線）②拼圖過程的本質是什么，主要目的是什么？（拼圖過程的本質就是圖形變換，主要目的就是用三個內角組成一個平角，實現未知角度的整合）

拼圖過程是相對直觀的教學活動，為引導學生進一步理解，有必要結合拼圖活動來理解整個過程，完成感性思維向理性思維的初步過渡，為后續的幾何證明打基礎. 如設置如下活動：將△ABC的三個內角撕下來后，可以采用如圖2的兩種方式將三角形的三個頂點拼接在同一處，請大家根據角的邊線繪制虛線，并思考虛線與∠B形成的幾個角分別對應原三角形中的哪個內角，進一步思考所繪制的虛線是否與原三角形的邊存在平行關系.

學生通過觀察很容易發現拼圖過程中角的對應關系，以及所繪制虛線BF與三角形的邊AC之間是平行關系，從而深刻理解拼圖的過程實際上就是等角轉化的過程，即實現三個內角平移到三角形所在平面的同一頂點處，從而得到平角. 上述活動中主要涉及兩大內容：一是移動拼圖，二是作輔助線. 前者是后續圖形變換的教學基礎，后者讓學生初步體驗了構造輔助線的過程，體會到輔助線參與的轉化策略.

以嚴密的幾何證明作為教學的

發展點

數學課堂的教學目的是培養學生的邏輯思維，讓學生形成嚴密的數學思維，因此教學中需要設置相應的環節使學生完成感性認識到理性思考的過渡. 在知識的發展階段需要銜接之前的拼圖活動，從拼圖中抽象出幾何模型，通過嚴密的幾何證明來強化學生認知，形成具有科學性的結論，這是教學的發展點.

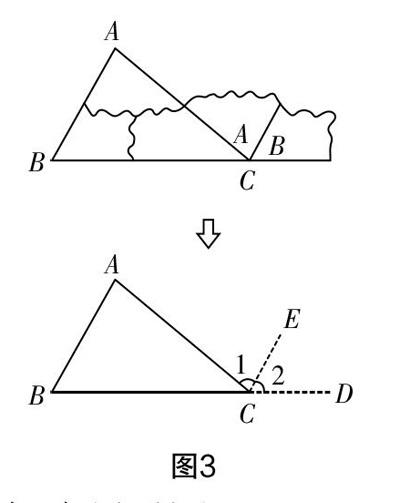
實際教學中利用拼圖模型來抽象出幾何模型，讓學生思考證明思路，可以設置如下活動：圖3所示是某位學生將三角形三個內角拼接在一起的過程，請根據該過程的證明思路完成幾何說理證明. 在實際教學中需要教師引導學生嚴格按照幾何構造、說理的方式來進行，具體如下.

[圖3]

已知：如圖3所示，∠A、∠B、∠C是△ABC的三個內角. 求證：∠A+∠B+∠C=180°.

證明：延長BC至點D，過△ABC的頂點C作邊AB的平行線EC，因為EC∥AB，所以∠1=∠A（兩直線平行，同旁內角相等），∠2=∠B（兩直線平行，同位角相等）. 因為∠C+∠1+∠2=180°，所以∠A+∠B+∠C=180°，證畢.

根據上述幾何證明過程，教學引導需要分三步進行：第一步引導學生按照拼圖思路繪制輔助線，即繪制與邊AB相平行的直線;第二步引導學生觀察分析圖中的∠1和∠A，∠2和∠B分別是同旁內角和同位角中的哪種關系;第三步引導學生利用兩線平行的性質定理來構建相應的等角關系，逐步完成等角代換證明.

為培養學生思維的靈活性和多樣性，在完成上述引導證明后，還可以讓學生從不同的角度、不同的方位思考證明三角形的內角和為180°的方法. 如給出圖4所示的拼圖示意圖，讓學生通過自我思考，小組討論的方式來完成圖中的說理證明，教師要適時對學生的說理進行糾正，提升學生的語言表述能力.

[圖4]

上述是從幾何證明角度來完成知識發展，在該過程中完成了文字語言和幾何語言之間轉化，這是需要學生在初中階段掌握的基本技能，對于學生今后的推理證明學習有著極大的幫助，因此在教學中教師需要關注學生的思維發展，有效把握學生的思維沖突來推進課堂教學.

以開放的例題變式作為能力

的提升點

“三角形的內角和”的教學中主要有兩大任務：一是使學生掌握相應的性質，學習證明過程，二是使學生掌握性質的應用方法. 對于后者需要以開放的例題來培養，這也是教學的能力提升點. 教學中需要適應學生的個性需要設置多變的例題，充分調動學生思維的變通性和創造性來加以解決.

問題設置需要從兩個角度進行：一是引導學生直接利用三角形的內角和性質來完成未知角的求解;二是從知識聯系性出發，引導學生結合相關知識，應用性質定理分析問題. 基于上述設計原則，設計如下兩道例題.

例1如圖5所示，在△ABC中，已知∠BAC=60°，∠C=45°，若AD是△ABC的角平分線，試求∠ADB的大小.

[圖5]

例題涉及三角形的內角和性質和角平分線性質，教學時首先需要引導學生根據角平分線的性質得出∠DAC的的大小，然后引導學生利用三角形的內角和性質推理出∠ADC的大小，最后由平角的意義來獲得答案. 在例題求解結束后，還可以引導學生進一步思考整個問題突破的思路，幫助學生形成新的解題策略.

例2已知△ABC中∠A ∶ ∠B ∶ ∠C=1 ∶ 2 ∶ 3，試求∠A、∠B、∠C的大小，并判斷△ABC的形狀.

對于該例題，教學中首先需要教師引導學生思考比例分配問題的求法，即通過設元的方法將三個角的大小表示出來，然后引導學生利用三角形的內角和性質構建相應的方程來求解. 該例題很好地體現了方程思想的應用，因此教學結束后可以引導學生總結方程思想解析問題的策略，即“設未知量→分析數量關系→建立方程→解方程求答案”.

考慮到方程思想解析問題的過程較為抽象，教學時需要教師結合具體的問題，例如對于上述試題，設∠A=x，則對應的有∠B=2x，∠C=3x;分析數量關系階段引導學生調用三角形的內角和性質，即三個內角之和為180°;建立方程階段只需要引導學生將三個內角之間的數量關系方程化即可，即x+2x+3x=180°;最后引導學生嚴格按照解方程的步驟求解.

利用開放的例題可以有效培養學生的思維能力，在例題教學時需要注重分析方法的滲透，引導學生掌握文字語言提煉、分段說理推斷、逐條演繹說理的方法，逐步使學生掌握相應的解題策略，形成良好的解析思維.

總之，“三角形的內角和”的教學需要在《數學課程標準》的基本理念指導下進行，準確把握課堂教學的起點、生成點、發展點和提升點，做好課堂教學引導，尊重學生的主體地位，使學生充分參與探究過程，使學生掌握相應知識的同時獲得能力的提升.