規律探究題的類型剖析與策略總結

王律奇

[摘? 要] 探究數學規律是發現新知的重要手段，對于思維的提升極為有利. 而近幾年的中考中出現了眾多的規律探究題，且題型靈活多樣，對學生的問題分析、知識總結能力要求較高，文章將剖析規律探究題的類型，探究問題的解法策略，以供讀者學習參考.

[關鍵詞] 規律探究題;解法策略

問題起源

初中階段的數學教學重點是指導學生掌握相應的知識，獲得解題的方法，另一個教學目標是拓展學生的思維，促進學生核心素養的發展，而后者應成為數學教學的核心. 其中培養學生的創造性思維尤為重要，而學習規律探究型問題是提升學生創造性思維的重要方式之一，學生在規律發現的過程中需要充分觀察、推理、歸納、猜想，因此對學生的思維有著極大的鍛煉. 同時新課程標準推行以來，規律探究題也逐步成為中考的熱點問題，因此深入探究規律探究題的問題類型和解法策略有著深遠的意義.

類型分析

初中數學的知識內容大致可以分為代數和幾何兩類，這個分類對于規律探究題同樣適用，中考在考查時只是做了進一步的細化，例如以數為基礎進一步衍生出數式類規律題、函數類規律題，以幾何為基礎衍生出圖形變換規律題、坐標變換規律題等，且每一類規律探究題均有其對應的特點.

1. 數式類

該類規律題一般以數的變化為重點，常見的呈現方式有兩種：一種是直接給出具有特定規律的數或算式，另一種是給出具有規律變化的代表個數的原點，均需要學生完善或進一步推演規律.

2. 函數類

函數類規律題則是以初中常見的函數知識為基礎，題干一般給出對應的函數關系或者關系式，需要學生結合自身對函數的理解對其加以完善，或推理出后續的函數關系式.

3. 圖形變換類

該類型是幾何綜合的代表，題干一般給出一系列具有關聯性的圖形，以及圖形生成的具體操作，需要學生結合幾何性質，從中發現衍生規律.

4. 坐標變換類

該類規律題最為特殊，一般是幾何與函數知識的綜合，以點坐標和線段長的變換作為圖形衍生遞推的基礎，以幾何性質和數式變化作為規律生成的媒介，且在直角坐標系中構建了相應的數形規律，因此規律的探究需要調用幾何與代數兩大知識模塊.

策略探究

規律探究題實際上就是初中數學代數與幾何的排列組合，其中必然隱含著數學規律，因此解題分析過程實際上就是使用合理的策略找到問題的突破口. 而對于不同類型的規律探究題，其解法策略也有所不同，下面結合考題對其加以深入解讀.

1. 策略一：舉例歸納，發現規律

對于一些以數值或算式為主體的規律探究題，最為快捷的方法是舉例驗證，即首先按順序列舉出數的運算過程和結果，然后歸納出規律，并對其加以驗證. 有時由于列舉的數值量不夠容易造成規律得出的錯誤，因此在列舉時應適當多舉例.

例1古希臘數學史上將1，3，6，10，15，21…叫三角形數，其中含有一定的規律，例如將第一個三角形數記作是a1，第二個三角形數記作a2，……，將第n個三角形數記作an，然后依次計算a2-a1，a3-a2，a4-a3…由此推算，試求a100-a99和a100的數值.

解析? 上述題目給出了相應的算式排列，解題的關鍵是分別計算出a2-a1，a3-a2，a4-a3的數值，并發現其中的規律，然后推導出a100-a99和a100的數值，顯然使用列舉法更為高效. 觀察三角形數可確定a2-a1=3-1=2，a3-a2=6-3=3，a4-a3=10-6=4，類推a5-a4=15-10=5，從而可推得a100-a99=100. 而a2-a1+a3-a2+a4-a3+…+a100-a99=，即a100-a1=5049，已知a1=1，所以a100=5050.

2. 策略二：排列類比，遞推規律

探究算式規律是代數類規律探究題的重要類型，題干一般會給出一系列的算式，因此在解析時可以按照一些順序對其加以排列，通過數列推導、類比參照的方式總結其中的通式，從而獲得最終答案.

例2? （2018年臨安中考）已知：2+=22×，3+=32×，4+=42×，5+=52×，…. 若10+=102×符合前面式子的規律，試求a+b的值.

解析? 題干給出了一些具有排列規律的數式，并對a和b進行了設定，求a+b的值可以采用排列類比的方式，分別獲得a和b所代表的通式，然后確定最終答案. 觀察題目給出了四個等式，類比總結可知對于，其中的b=n+1，而a=（n+1）2+1（其中的n表示對應的第n項式），因此對于第10項可知b=10，a=99，所以a+b=109.

3. 策略三：關注特征，循序歸納

幾何類規律題必然涉及幾何特征或對應性質，因此在分析該類問題時需要充分把握圖形的特征結構，適當結合幾何性質，根據圖形的變化特點來逐步發現其中的變化規律，并對其加以總結.

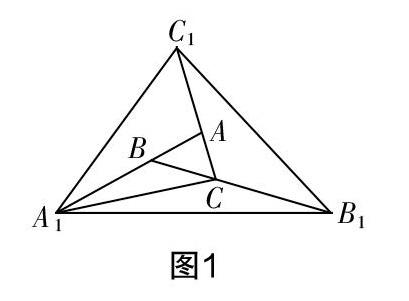
例3如圖1所示，△ABC的面積為1，現對其逐次進行如下操作變形：

第一次，將AB，BC和CA分別延長至點A1，B1，C1，并使得A1B=2AB，B1C=2BC，C1A=2CA，然后順次將點A1，B1，C1連接起來，從而得到了△A1B1C1，并記△A1B1C1的面積為S1;第二次進行同樣的操作，將A1B1，B1C1和C1A1分別延長至點A2，B2，C2，并使得A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，然后順次將點A2，B2，C2連接起來，從而得到了△A2B2C2，并記△A2B2C2的面積為S2……之后一直按照上述規律進行操作，可以得到△A5B5C5，試求△A5B5C5的面積S5的值.

解析? 本題目屬于幾何變化規律探究題，首先需要理解作圖的具體操作，關注圖形的特征及關聯，然后利用相應的幾何知識發現其中的規律. 第一步中表明A1B=2AB，而△A1BC與△ABC可以視為是以點C為頂點，底邊共線的關聯三角形，因此兩三角形底邊上的高相等，其面積大小只與底邊長有關，即S△A1BC=2S△ABC，同理可確定S△A1B1C=2S△A1BC，可得S△A1B1B=6S△ABC，以此類推，可確定S△C1B1C=6S△ABC，S△A1C1A=6S△ABC，所以S△A1B1C1=19S△ABC . 最后按照這樣的推理可計算出S5=195=2476099.

4. 策略四：數形結合，衍生規律

而對于以直角坐標系為基礎構建的圖形變化規律，考慮到其中涉及幾何變化和點坐標、線段長的遞變，因此采用數形結合的解題策略更為有效. 即首先從“形”的角度理解圖形變化，提取其中的幾何特征，然后從“數”的角度，借助直角坐標系將點和線的變化數量化，并構建相應的規律模型，最終實現求解.

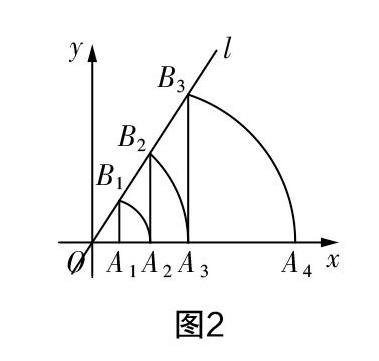
例4（2018年廣西貴港中考）如圖2所示，直線l為y=x，過點A1（1，0）作A1B1⊥x軸，與直線l交于點B1，以原點O為圓心，OB1長為半徑畫圓弧交x軸于點A2;再作A2B2⊥x軸，交直線l于點B2，以原點O為圓心，OB2長為半徑畫圓弧交x軸于點A3;……，按此作法進行下去，試求點An的坐標.

[圖2][O][x][y][A1][A2][A3][A4][B3][B2][B1][l]

解析? 本題目是以直角坐標系為背景展開的幾何衍生，需要確定A系列點的坐標規律，實際上屬于線段的長度規律題. 考慮到A系列點均位于x軸上，因此只需要歸納出OAn的長度通式即可. 首先閱讀題干操作，可知線段AnBn均垂直于x軸，B系列點均位于直線l上，而△OAnBn均屬于直角三角形，且∠O=60°，因此可利用直線l的解析式確定B系列點的坐標. 如對于點B1，由點A1（1，0）可得點B1（1，）. 在Rt△A1OB1中使用三角函數，可知OB1==2，即OB1=2OA1=2，而根據扇形的性質可得OB1=OA2，即點A2（2，0），依次遞推可得A2（4，0），A3（8，0）A4（12，0），顯然A系列點的橫坐標值符合常見的數列規律，即xAn=2n-1，所以點An的坐標為（2n-1，0）.

解后思考

規律探究題的類型很多，涉及的知識點眾多，因此掌握合理的解題策略，利用合適的分析方法開展規律探尋是解題的關鍵所在. 上述只是其中較為常用的幾種解法策略，而在實際教學中需要教師逐步引導，幫助學生建立相應的解題思路，主要有以下幾點.

1. 重視讀題，提取信息

一般規律探究題會給出大量的圖文信息，因此理解所給信息的含義是后續推理的基礎，例如理解數據變化、圖形衍生的過程、直角坐標系中線段繪制的操作等，然后從圖形和文字兩方面來提取信息. 因此在實際教學中需要教師強調讀題重點，指導讀題、信息提取的技巧，幫助學生養成良好的讀題習慣.

2. 重視歸納，知識調用

規律探究題的第二個階段是對所提取的信息進行歸納，然后利用自身所學知識來分析其中的規律. 例如對于直角坐標系中的數形變化規律題，從中可以提煉出關于點坐標、線段長、幾何面積等信息，而這些信息鏈之間存在著一定的關聯性，因此需要學生對其加以歸納，并利用所學知識進行分析. 而在教學中教師應從基礎知識入手，引導學生關注知識間的聯系，建立相應的知識網絡.

3. 重視提煉，總結規律

規律題探究最為重要的階段是對歸納的規律進行提煉生成，例如總結出相應的數式通式，點坐標的計算通式，將其上升到一般適用的規律層面. 這個階段需要利用一定的提煉技巧，例如類比法，函數衍生法等. 而在教學中需要教師呈現規律提煉的具體過程. 讓學生掌握提煉的技巧，提升學生的知識總結能力.