基于連續Hopfield網絡的復雜網絡社團結構提取

代婷婷，董延壽，韓 艷

（昭通學院數學與統計學院，云南昭通 657000）

一個是1998年Watts和Strogatz發表在Nature上的文章〔1〕揭示了復雜網絡的小世界特性；另一個是1999年Barabási和Albert發表在Science上的文章〔2〕揭示了復雜網絡的無標度性質，認為網絡的這種性質緣于兩個缺一不可的演化要素，并據此提出了一個網絡模型，傳統的網絡模型是建立在隨機圖基礎上的〔3〕。

對于復雜網絡的研究主要是研究其社團結構，關于復雜網絡中的社團結構提取有很多的算法。Girvan 和 Newman〔4〕在2002年提出了一種通過邊移除按層次分解網絡的社團結構方法（GN）。此項研究工作被認為是現代社團結構研究的開創性工作，各研究領域的研究員對此有著廣泛的興趣。GN算法尋找最可能處于社團之間的邊，通過不斷地將這些邊移除得到網絡的層次劃分。Radicchi等〔5〕針對GN算法進行了一些改善，提出了一個新的GN自包含算法。

1 算法

1.1 連續神經網絡求解矩陣的特征值及特征向量考慮微分方程

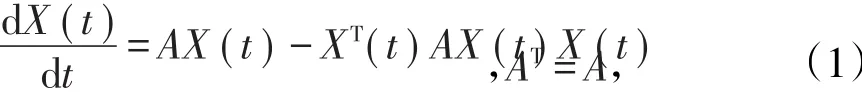
其中，A是一個n×n的實對稱矩陣，可以將其視為神經網絡的連接權強度，X∈Rn，視為神經網絡的狀態，那么方程（1）就描述了一類連續型的全反饋人工神經網絡。Radicchi等〔5〕給出了一種電路模擬方法，當A為對稱正定矩陣時，OJA等〔6〕根據神經網絡的Hebbian規則，將方程（1）作為一種無教師指導的神經網絡學習過程，研究了輸入空間提取特征主元的問題，證明了方程（1）從任意初始值出發的解都收斂于A的最大特征值對應的特征向量。這個可以由下面的定理保證。

定理1假設A的最大特征值λ＞0，則式（1）的從任意初值X(0)Rn出發的解均收斂于A的最大特征值λ對應的特征向量〔7〕。

該定理給出了一種新的求解矩陣特征值和特征向量的方法。

1.2 社團提取問題中的模塊度函數假定網絡包含有n個節點，對于一個網絡進行特殊的劃分，即將網絡劃分為兩個組，讓si=1表示節點i屬于第一組，當si=-1時，表示節點i屬于第二組。將節點i和節點j之間邊的連接數目表示為Aij（其值取0和1）。若網絡中有重邊存在，則Aij可以取比1大的值。Aij就是所謂的網絡鄰接矩陣中的元素，若節點i和節點j之間邊的連接是隨機的，則均值為kikj/2m，ki表示節點i的度，i=1,2,...,n，m=表示網絡中邊的總數目，則文獻〔7〕中的社團提取問題中模塊度函數Q可定義為

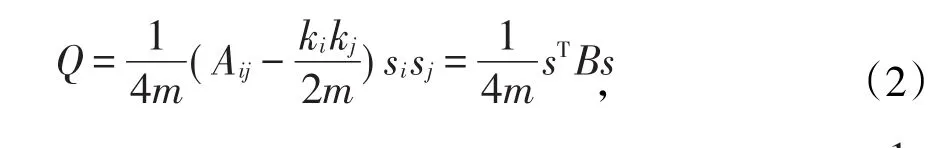
這里s表示向量，其第i個元素為si，i=1,2,...,n是個常數。而對稱矩陣B稱為模塊度矩陣，其元素為：

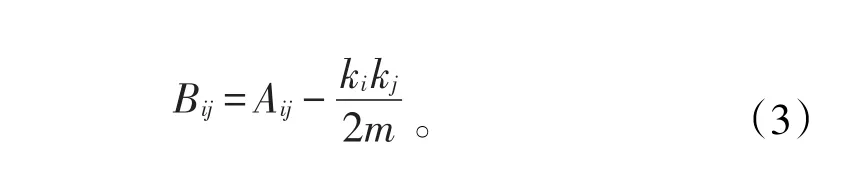
利用（3）式將矩陣B進行化簡發現它的行和與列和都為零，因此矩陣B總有特征向量(1,1,1,...)，其對應的特征值為0，這是拉普拉斯圖矩陣的性質〔7〕，也是圖分割的基礎。

1.3 連續神經網絡提取復雜網絡社團結構的算法（CNN） Newman〔7〕將模塊度函數Q定義為（2）式，模塊度矩陣B定義為（3）式，若考慮復雜網絡為無向網絡，則鄰接矩陣A是一個實對稱矩陣，從（3）式可知模塊度矩陣B也是一個實對稱矩陣，所以根據Fortunato等〔8〕的闡述，可以利用方程（1）的神經網絡系統求解出模塊度矩陣B的最大特征值對應的特征向量，與此同時，結合Newman的特征值特征向量提取社團結構的算法的原理，就可以不用計算模塊度矩陣B的最大特征值對應的特征向量，而直接通過解微分方程（1），利用微分方程（1）的解中元素的符號就可以將復雜網絡中的節點分為兩類。據此，提出了如下CNN算法。

針對復雜網絡的社團結構檢測問題，將Newman的基于模塊度函數Q的矩陣特征值和特征向量提取復雜網絡中社團結構的算法和神經網絡算法求解矩陣特征值特征向量的算法結合起來得到一種新的基于連續神經網絡的社團結構檢測算法，簡稱CNN算法，模型為：

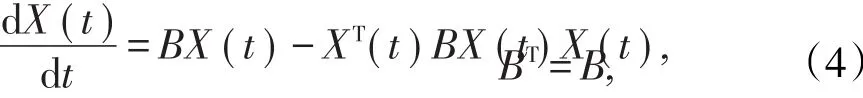
其中，B為（2）式定義的復雜網絡的模塊度矩陣，X∈Rn，由定理1知，從任意初值出發，方程（3）的解都會收斂到模塊度矩陣B的最大特征值對應的特征向量。結合Newman的特征值特征向量算法，就可以根據方程（3）的解中元素的符號將復雜網絡中的社團結構提取出來。

綜上所述，設復雜網絡的鄰接矩陣為A，本文給出的基于CNN的社團結構提取算法的步驟如下：

步驟1：計算復雜網絡的模塊度矩陣B，其中的元素為 ，ki表示節點i的度，ij表示復雜網絡的鄰接矩陣A的元素；X(0)=BX(t)-

步驟2：給定任意初值 ，求解XT(t)BX(t)的X(解t)X?；

步驟3：根據解X?得到社團結構標簽向量s，其中向量s中的元素如下確定

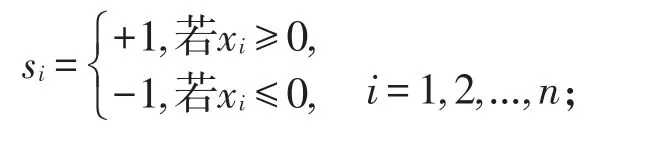
步驟4：將s中+1對應的節點提取出來。

2 結果

2.1 實驗數據在本文中，采用了空手道俱樂部網絡（Zachary's Karate Club Network）〔9〕數據做實驗。該網絡數據的下載網址是 http：∕www-personal.umich.edu∕～mejn∕netdata∕。

空手道俱樂部網絡：在社團提取問題中空手道俱樂部網絡是被應用最為廣泛的例子之一。空手道俱樂部網絡由34個節點組成，每個節點表示一個成員，網絡中的78條邊表示成員之間的社會交往關系，由于俱樂部主管和校長之間發生矛盾，俱樂部成員就被分成了分別以主管和校長為中心的兩個社團。

2.2 實驗結果及分析在實驗部分，將在俱樂部網絡上分析連續神經網絡算法的穩定性以及分類效果，分別選出俱樂部網絡中所有的節點和某幾個節點分析CNN算法的穩定性，結果見圖1～2。

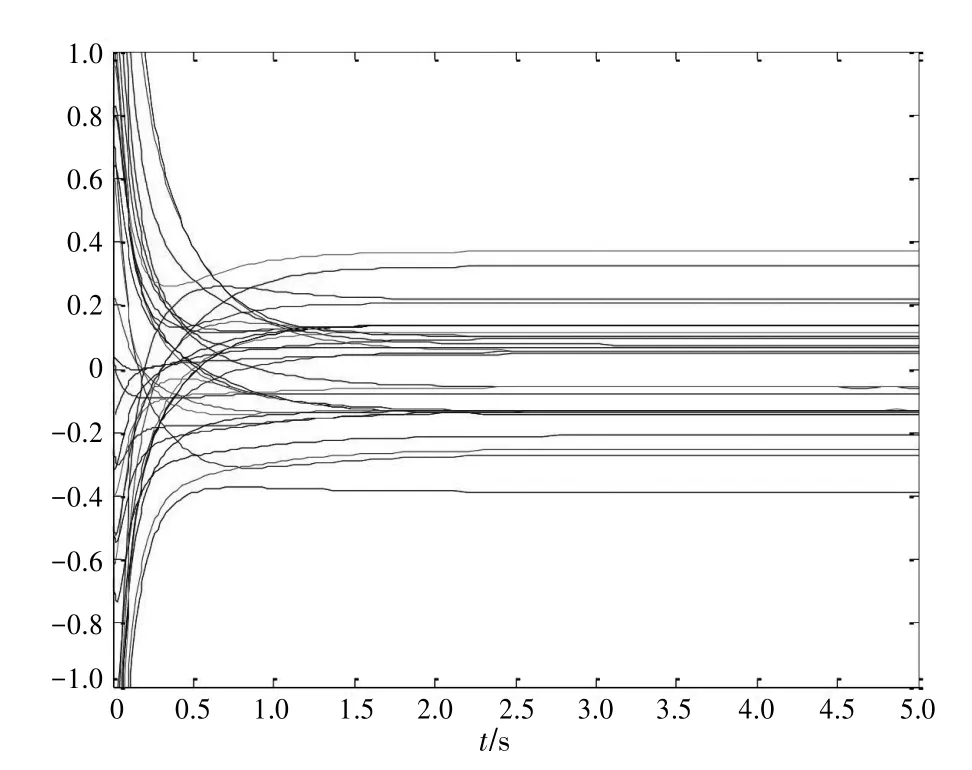
圖1 CNN算法在空手道俱樂部網絡上的穩定性分析

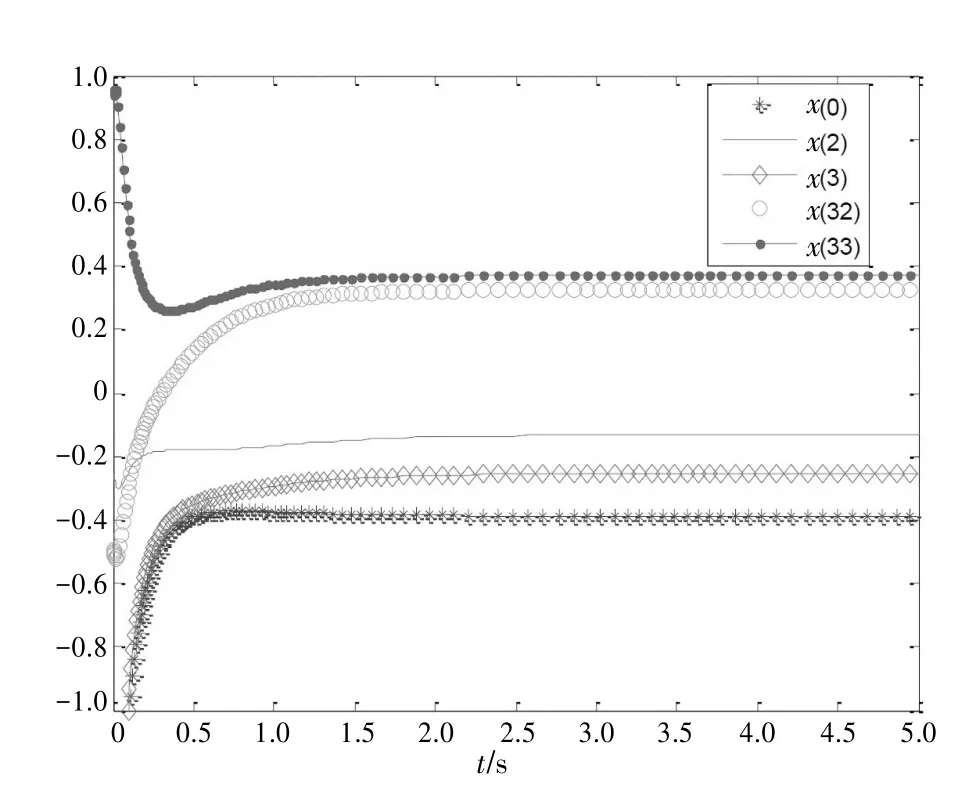
圖2 CNN算法下空手道俱樂部網絡上某幾個點的穩定性分析

從圖1可以看出，當t=0時，對于任意的初始值X(0)，隨著時間的推移，發現俱樂部網絡中的每個節點所對應的網絡狀態最終收斂到一個穩定狀態，即收斂到俱樂部網絡的模塊度矩陣B的最大特征值對應的特征向量。因此根據網絡穩定狀態的符號提取出俱樂部網絡中的社團結構。從圖2可以更清楚地看到CNN網絡中的某幾個狀態的收斂情況，給定任意的初值X(0)后，只需1.5s,網絡中的0、2、3、32、33這5個節點的網絡演進就達到了穩定狀態。這表明CNN算法的穩定性良好。

采用連續神經網絡算法提取空手道俱樂部網絡中的社團結構，結果見圖3。

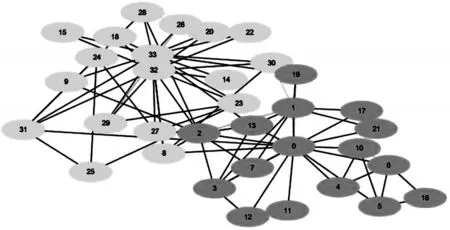
圖3 連續算法提取空手道俱樂部網絡中社團結構的分類結果

圖3列出了連續神經網絡算法在空手道俱樂部網絡上的仿真結果。從實驗結果發現，特征向量算法、連續算法對空手道俱樂部網絡的分類結果與特征向量算法的分類結果（Q=0.3715）相同，表明本文中的算法也是合理的。

3 討論

復雜網絡是研究復雜系統的有力工具，很多現實的系統都可以抽象成復雜網絡來研究，網絡的節點對應著系統中的實體。研究表明，很多真實網絡中存在著不同程度的社團結構特性，而這種社團結構決定著網絡的某些功能屬性，因此在網絡中描述和檢測這些社團結構具有重要的實際意義。本文立足于檢測復雜網絡中的社團結構這個課題，提出了基于模塊度函數Q這個指標的社團結構提取算法——連續神經網絡算法，并且將該算法和已有的相關算法作了比較，表明了此算法的有效性。