初中數學幾何原創題的思考

盛元

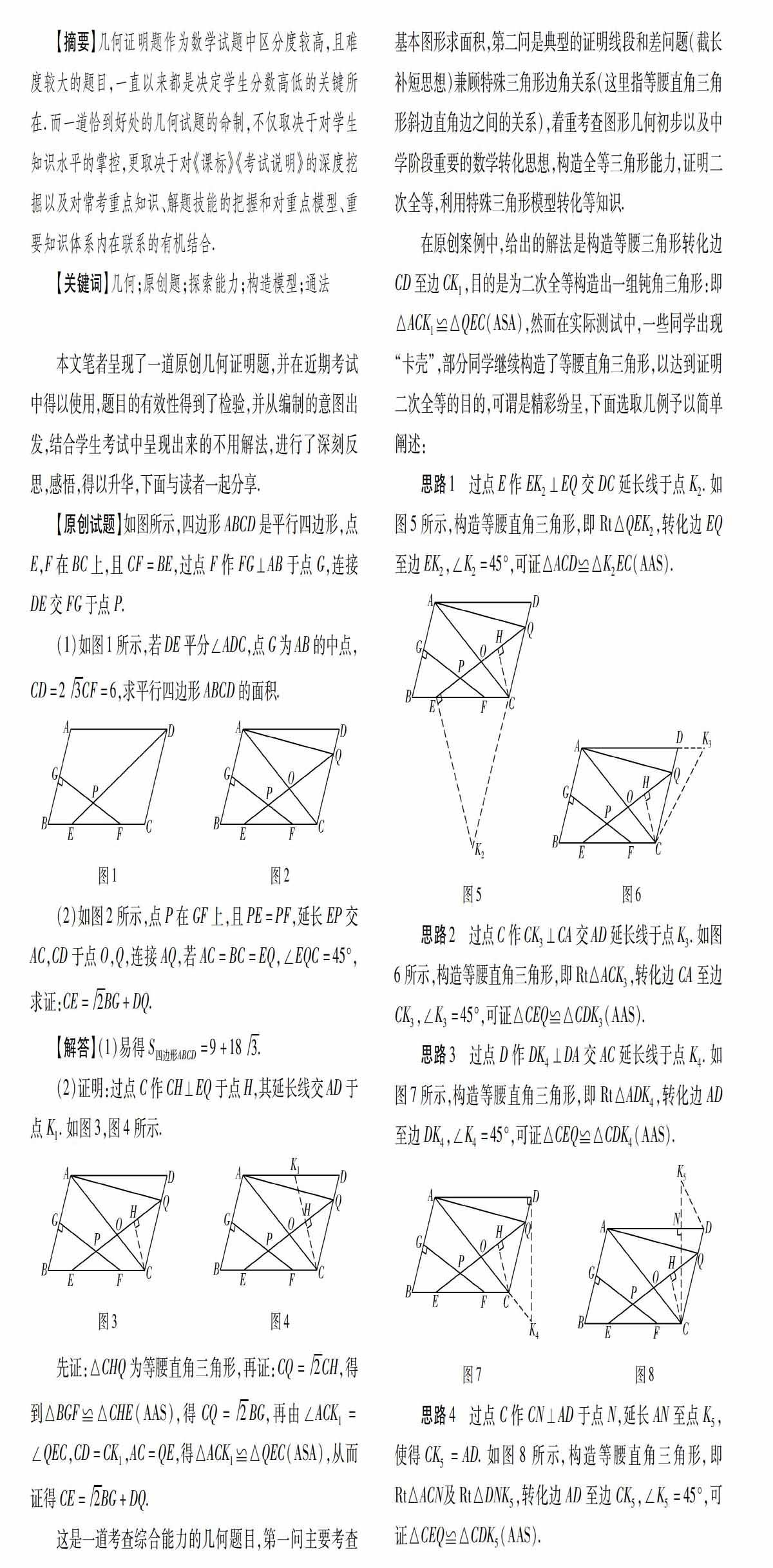
【摘要】幾何證明題作為數學試題中區分度較高，且難度較大的題目，一直以來都是決定學生分數高低的關鍵所在.而一道恰到好處的幾何試題的命制，不僅取決于對學生知識水平的掌控，更取決于對《課標》《考試說明》的深度挖掘以及對常考重點知識、解題技能的把握和對重點模型、重要知識體系內在聯系的有機結合.

【關鍵詞】幾何;原創題;探索能力;構造模型;通法

本文筆者呈現了一道原創幾何證明題，并在近期考試中得以使用，題目的有效性得到了檢驗，并從編制的意圖出發，結合學生考試中呈現出來的不用解法，進行了深刻反思，感悟，得以升華，下面與讀者一起分享.

【原創試題】如圖所示，四邊形ABCD是平行四邊形，點E，F在BC上，且CF=BE，過點F作FG⊥AB于點G，連接DE交FG于點P.

1.命題意圖闡述

基于初三數學階段性復習的考查，立意明確，考點突出，以平行四邊形為載體，依托三角形全等考查幾何能力.

2.從《課標》要求分析

（1）《課標》的知識技能要求：探索并掌握相交線、平行線、三角形、四邊形的基本性質與判定，掌握基本的證明方法和基本的作圖技能.數學思維方面，體會通過合情推理探索數學結論，運用演繹推理加以證明的過程，在多種形式的數學活動中，發展合情推理與演繹推理的能力.能力方面，能獨立思考，體會數學的基本思想和思維方式，體會模型思想.問題解決方面，經歷從不同角度尋求分析問題和解決問題的方法的過程，體驗解決問題方法的多……