基于IWRAP模型的船舶交通流數據擬合模型

柯冉絢， 胡栩禎， 陳 毅

(集美大學 航海學院，福建 廈門 361021)

伴隨船舶大型化、交通流密集化等問題，航道的風險管理日趨重要，科學的管理是保障船舶安全行駛的有效途徑。[1]在船舶交通流統計的基礎上，使用IWRAP模型計算水域的船舶碰撞和擱淺的概率，對于了解水域的安全情況具有重要意義。[2]

吳兆麟[3]采用港口或選定水域的交通流數據，將對某一特定時期內(如季度或年度)所發生的船舶交通事故數量與該期間內船舶活動量的比值作為衡量該港口或水域在該期間內的船舶交通安全狀況的指標。孫苗等[4]根據水域轄區內的交通流情況，提出利用船舶交通服務(Vessel Traffic Service, VTS)系統設置船舶可能存在的擱淺判定條件，指導相關人員及時向存在擱淺風險的船舶發出預警信息，及時提醒船舶人員采取應對措施。黃純等[5]借助長江口水域2010—2015年的交通流數據，實際數據發生船舶碰撞事故為21.8起/a，擱淺事故頻率平均為1.8起/a；使用IWRAP MKII軟件的計算結果是碰撞事故平均為21.05起/a，擱淺事故頻率平均為2.298起/a，計算結果與實際情況比較相符。

已有的研究較少涉及安全評價的定量分析；另外，已有的定量研究在使用IWRAP MKII軟件時，主要關注模型運行結果與實際是否相符，本文則側重于以交通流分布函數的擬合度，即選擇數據的分布函數這個起源，探究模型運行結果的可靠性，提出模型擬合優化的方法，提供更好應用IWRAP MKII軟件分析水域風險的思路。

1 IWRAP模型基礎理論

加拿大海岸警衛隊和丹麥科技大學聯合開發的航道風險評估工具IWRAP(IALA Waterway Risk Assessment Program)是一種以事故致因概率為前提， 基于船舶自動識別系統(Automatic Identification System, AIS)歷史數據對船舶碰撞和擱淺概率進行理論計算的模型，它可以有效地對在不同航段中的不同類型的船舶碰撞和擱淺的概率進行計算和分析比較，并進行預測。

1.1 潛在碰撞船舶數量計算模型

碰撞可以簡單地分為兩種類型：發生在直線航段碰撞，即對遇碰撞和追越碰撞；發生在交叉航段的碰撞，即交叉碰撞。針對兩種不同的碰撞方式，該模型運用不同的計算方法。

1.1.1直線航段計算模型

在直線雙向航道上，沿航線航行的船舶發生幾何碰撞事故的潛在船舶數量為

(1)

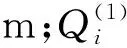
(2)

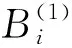
若f(yi)(1)和f(yj)(2)都是正態分布，且其分布參數分別為(μi,σi)和(μj,σj)，則對遇潛在碰撞船舶數量的計算式可簡化為

(3)

(4)

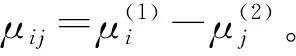
1.1.2彎曲航段計算模型

IWRAP模型中，將兩船夾角為 10°～170°時定義為交叉相遇，兩船在交叉相遇的過程中發生碰撞的情形見圖2。在交叉航道上，船舶發生幾何碰撞事故的潛在船舶數量可表示為

(5)

1.2 潛在擱淺船舶數量計算模型

擱淺分為操縱性擱淺和漂移性擱淺兩類。操縱性擱淺是由于人為錯誤或者船員缺乏警惕性造成的(第I類)；漂移性擱淺是由于操作或者推進裝置失效，船舶失去自航能力造成的(第II類)。水域內的預計擱淺事件或與固定物體碰撞的預計次數的模型見圖3。

根據模型，上述擱淺類別中預計擱淺事件數量為

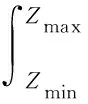
(6)

(7)

式(6)和式(7)中：ai為導航器進行2次定位的平均距離；d為導航路線中從障礙物到航線轉彎的距離，隨著船舶的橫向位置s而變化；i為船舶種類，按船舶類型和自重或長度分類;fi(z)為船舶交通的概率密度函數；NI為預計每年I類擱淺事件的數量；NII為每年預計第II類基準事件的數量；Pc,i為因果概率，即在擱淺過程中船舶擱淺和船舶之間的比率；Qi為第i級船舶每年通過路線橫斷面的數量；Z為垂直于航道方向的坐標；Zmin，Zmax分別為障礙物的橫向坐標。[6]

2 風險建模與評估流程

2.1 風險的基本概念和量化方法

指定海域中通航的船舶交通風險，該風險顯示為此航線上通行的船舶發生碰撞或擱淺的概率，并量化為某個指定的時間段內發生該事故數。

通過對指定航線上航行的船舶進行碰撞和擱淺頻率的評估進行風險的量化。首先確定航線和水域，之后導入相關的AIS數據，分析該水域的交通流分布函數，與IWRAP MKII軟件中提供的7種交通流分布函數進行擬合，經分析和比較，選擇最符合實際數據的擬合曲線，然后在IWRAP MKII軟件中運行，計算該水域所有船舶碰撞和擱淺的概率，且進行驗證，從而提高應用該模型算法計算船舶碰撞概率的準確度，為選定的水域內船舶風險評估提供參考。

2.2 IWRAP MKII簡介

IWRAP MKII應用程序是為用戶提供一個評估指定水域內船舶碰撞和擱淺風險的量化工具。IWRAP MKII允許設置不同的場景，評估因交通流量和交通流的組成發生變化，或者航道幾何結構變化，或者助導航設施的變化，或者其他緩解風險的選項也變化的情況下，碰撞和擱淺年平均數量(概率)產生的變化。IWRAP MKII是基于MS-WindowsTM的應用程序實施的，其風險評估流程涉及以下步驟[7-8]：

1) 定義水深、航線、航點和航段。

2) 在每條航道輸入交通流分布。

3) 定義每條航段的船舶統計分布。

4) 標識漂移引起的擱淺。

5) 定義該地區的其他交通。

6) 選擇概率影響因素。

7) 結果計算和評估。

使用廈門港2016年的AIS數據進行擬合，并運行IWRAP MKII軟件，進行數據分布函數擬合的分析和比較，以此說明分布函數擬合度越好，該軟件運行的結果與實際風險情況的相似度越高。

3 廈門港交通流數據的統計分析

3.1 廈門港的進港和出港數據圖示分析

本文使用的交通流數據來自2016年廈門港主航道內進出港集裝箱船舶的VTS截面數據基礎上預處理過的數據。數據的處理是在定義航段基礎上進行的，所定義的航段在廈門港九節礁附近的主航道上，該航段交通流較為密集，是船舶進出廈門港的必經之路。

根據廈門港2016年的集裝箱船交通流數據，將交通流數據分為進港和出港兩部分，在EXCEL中畫出直方圖，結果見圖4和圖5。從圖4和圖5可知：廈門港進出港的交通流分布呈先上升再下降的趨勢，與IWRAP MKII軟件中的7種曲線—Normal(正態分布)曲線、Gumbel(max)(極大值)曲線、Gumbel(min)(極小值)曲線、Lognormal(對數正態分布)曲線、Uniform(均勻分布)曲線、Weibull(韋伯分布)曲線、Beta(貝塔分布)曲線對比而言：7種曲線中，Uniform(均勻分布)函數呈水平直線趨勢，其余6種分布函數曲線均呈先上升后下降趨勢。圖4和圖5的分布圖表明廈門港集裝箱船進出港的分布并非Uniform(均勻分布)。因此，初步的分析中，先把Uniform(均勻分布)曲線排除，然后將實際數據與其余6種曲線的分布進行比對。

3.2 交通流數據與各曲線的相關性

3.2.1 相關系數簡介

相關系數是反映變量之間關系密切程度的統計指標，按積差方法計算，以兩變量與各自平均值的離差為基礎，以兩個離差相乘來體現兩變量之間的相關程度。

相關系數一般用字母r表示，度量兩個變量間的線性關系，其定義式為

(8)

式(8)中：Cov(X,Y)為X與Y的協方差；Var[X]為X的方差；Var[Y]為Y的方差。

相關系數表示X和Y之間線性關系的緊密程度，定量體現X和Y的相關程度，即相關系數越大，相關程度越大。相關系數等于0表示相關程度最低，通常認為X和Y不存在線性關系。需要注意相關系數的正負號只表示相關的方向，絕對值為相關的程度。利用相關系數的性質計算廈門港交通流數據分布和各分布函數的相關系數并進行對比，篩選與廈門港實際交通流數據分布最接近的函數曲線。

3.2.2 廈門港進港船舶數據

在MATLAB軟件中使用corrcoef函數計算兩個序列的相關度，corrcoef(x，y)表示序列x和序列y的相關系數，得到的結果是一個2×2矩陣，其中對角線上的元素分別表示x和y的自相關，非對角線上的元素分別表示x與y的相關系數和y與x的相關系數，兩者相等。

使用corrcoef函數時，兩個序列的元素個數應相同。先設定一個隨機數列，然后用corrcoef(x，y)得出兩數列的相關系數。

將廈門港進港船舶數據導進MATLAB軟件，進行這些數據的分布與IWRAP MKII中6個分布函數的相關系數計算。

1)與Normal(正態分布)函數相關系數的計算。生成3 180×1的正態分布矩陣數據，以z=corrcoef(A,B)指令計算相關系數，zNormal=0.008 9。

2)與Weibull(韋伯分布)函數相關系數的計算。生成3 180×1的韋伯分布隨機矩陣數據，然后以z=corrcoef(A,C)指令計算相關系數，zWeibull=0.002 1。

3)與Lognormal(對數正態分布)函數相關系數的計算。生成3 180×1的對數正態分布隨機矩陣數據，然后以z=corrcoef(A,D)指令計算相關系數，zLognormal=0.003 1。

4)與Beta(貝塔分布)函數相關系數的計算。生成3 180×1的Beta(貝塔分布)隨機矩陣數據，然后以z=corrcoef(A,E)指令計算相關系數，zBeta=-0.004 3。

5)與Gumbel(max)(極大值)函數相關系數的計算。生成3 180×1的Gumbel(max)(極大值)函數隨機矩陣數據，然后以z=corrcoef(A,F)指令計算相關系數，zGumbel(max)=-0.007 7。

6)與Gumbel(min)(極小值)函數相關系數的計算。生成3 180×1的Gumbel(min)(極小值)函數隨機矩陣數據，然后以z=corrcoef(A,G)指令計算相關系數，zGumbel(min)=-0.003 3。

比較以上相關系數的絕對值，可知zNormal>zGumbel(max)>zBeta>zGumbel(min)>zLognormal>zWeibull，6個函數中，廈門港的進港集裝箱船舶分布與Normal(正態分布)函數相關程度最高，故之后將采用正態分布函數來表示2016年廈門港的進港集裝箱船舶數據分布。

3.2.3 廈門港出港船舶數據

出港數據與進港數據計算過程類似。首先將廈門港出港船舶數據導進MATLAB軟件，在MATLAB軟件中進行計算，形成一個3 188×1的矩陣，得出以下結果。

1)與Normal(正態分布)函數相關系數為zNormal=-0.005 2。

2)與Weibull(韋伯分布)函數相關系數為zWeibull=0.007 2。

3)與Lognormal(對數正態分布)函數相關系數為zLognormal=0.009 8。

4)與Beta(貝塔分布)函數相關系數為zBeta=0.001 1。

5)與Gumbel(max)(極大值)函數相關系數為zGumbelmax=0.005 6。

6)與Gumbel(min)(極小值)函數相關系數為zGumbelmin=0.002 3。

通過對比上述相關系數的絕對值結果，可知zLognormal>zWeibull>zNormal>zGumbelmax>zBeta，即在6個函數中，廈門港出港集裝箱船舶的分布與Lognormal(對數正態分布)函數相關程度最高。以上可見，進出港數據擬合分別匹配不同的分布函數，這也是在使用IWRAP MKII模型時需要留意的。

4 實例應用與驗證

通過IWRAP MKII軟件計算出廈門港2016年碰撞事故數并與實際發生的碰撞事故數進行對比，其差值越小，代表越接近實際情況，驗證選擇的交通流數據的分布函數曲線與實際交通流數據分布的擬合程度越高，使用IWRAP MKII計算船舶碰撞和擱淺的次數與實際更相符，即軟件評估風險的準確性越高。

4.1 廈門港主航道地形數據建模

地形數據建模包括構建出海圖上出現的島嶼、暗礁和陸地等，必須使用IWRAP MKII軟件自帶的多邊形工具手動構建。根據軟件中的Google地圖并結合廈門港九節礁附近的主航道海圖建模見圖6。

4.2 交通流分布建模

關于島嶼、暗礁、淺灘、陸地等構建完成后開始設置交通流信息。從上述結果可知，進港方向數據最接近Normal(正態分布)函數，出港方向最接近Lognormal(對數正態分布)函數。驗算分兩部分：第1部分在東向(進港)的數據設置上選擇Normal(正態分布)曲線，在西向(出港)上分別選擇不同的曲線Normal(正態分布)曲線、Gumbel(max)(極大值)曲線、Gumbel(min)(極小值)曲線、Lognormal(對數正態分布)曲線、Weibull(韋伯分布)曲線、Beta(貝塔分布)曲線完成計算；第2部分在西向(出港)的數據設置上一直保持選擇Lognormal(對數正態分布)曲線，在東向(進港)上選擇不同的曲線完成計算，以達到單一變量的效果，確保驗算的一致性。交通流分布設置界面部分截圖見圖7。

航段內交通流量是根據交通流量分布編輯器進行設置的。交通流量分布編輯器主要設置航段內每年船舶航行的數量、船舶的類型和船舶航行速度等相關設置。

IWRAP MKⅡ軟件默認在原油油船、成品油油船、化學品船、天然氣船、集裝箱船、雜貨船、散貨船、滾裝船、客船、快速渡船、支持船、漁船、油船、其他船對這14種船型進行區分，每種船型按25 m間隔分為若干個長度類別，分別為0～25 m，25～50 m，…，400 m及以上。此次計算的基礎數據為集裝箱船舶數據，填入集裝箱船的交通流量分布即可。

廈門港進港方向集裝箱船舶分布統計見圖8，廈門港出港方向集裝箱船舶分布統計見圖9。設置完成后，由MATLAB軟件運行進行計算。

4.3 評估結果分析與驗證

基本參數設置完成后，計算結果見圖10，東向(出港)數據設置保持不變，6種曲線對應的碰撞事故分析結果如圖10所示。

從圖10可看出：選擇Beta(貝塔分布)曲線計算結果為1.568起/a、選擇Weibull(韋伯分布)曲線計算結果為1.806起/a、選擇Lognormal(對數正態分布)曲線計算結果為1.933起/a、選擇Gumbel(min)(極小值)曲線計算結果為1.553起/a、選擇Gumbel(max)(極小值)曲線計算結果為1.709起/a、選擇Normal(正態分布)曲線的計算結果為1.648起/a，已知實際上2016年的碰撞事故6起，計算與實際碰撞事故數的差值并比較可以得出，選擇運用Lognormal(對數正態分布)曲線所進行的運算結果與實際最為接近。

同理，在西向(出港)數據設置不變情況下，6種分布曲線對應的計算結果為：選擇Beta(貝塔分布)曲線計算結果為1.683起/a、選擇Weibull(韋伯分布)曲線計算結果為1.234起/a、選擇Lognormal(對數正態分布)曲線計算結果為1.318起/a、選擇Gumbel(min)(極小值)曲線的計算結果為1.525起/a、選擇Gumbel(max)(極小值)曲線計算結果為1.745起/a、選擇Normal(正態分布)曲線計算結果為2.032起/a，已知實際上2016年的碰撞事故6起，計算與實際碰撞事故數的差值并比較可得出，選擇運用Normal(正態分布)曲線所進行的運算結果與實際最為接近。

統計學理論認為交通流分布數據服從正態分布函數，但是本范例通過廈門港2016年的數據分析后認為，實際上船舶航跡分布不是典型的正態分布函數，因此，應先進行交通流分布函數的擬合，選擇最為接近的分布函數。函數的選擇影響建模后的運行結果與實際結果的差距，函數越接近實際數據的分布增加，建模的差距就越小，計算結果也就越接近實際情況。

5 結束語

定量型航道風險評估工具IWRAP是IALA(The International Association of Marine Aids to Navigation and Lighthouse Authorities)推薦使用的航道風險管理工具。本文關注IWRAP模型中的交通流數據建模，建模過程中需要輸入船舶交通流分布，通過計算、對比與分析發現，從AIS導出的船舶交通流數據，部分接近正態分布函數，部分非正態分布，而現有的一些研究基本將其歸為正態分布。IWRAP MKII軟件運算結果顯示，分布函數擬合的相關系數越大，得出的風險預測結果就越接近實際。因此，在運用IWRAP MKII軟件的時候，應根據具體的交通流數據先進行分析對比，選擇擬合度較好的分布函數，從而更有效地發揮IWRAP模型的作用。

囿于基礎數據是AIS導出的數據，實際上可能存在AIS數據缺失或屏蔽AIS信息的船舶，以及不規則交通流的影響等，本文在分析和比較分布函數的選擇對于IWRAP模型運算結果的影響時，設置單一變量，從而避免其他因素的影響，因此即便IWRAP MKII軟件驗證過程中得到的碰撞結果與實際值存在差異，但并不影響擬合函數對比分析的可行性。后續研究可以增加水域內多個航段的設置，以及多種船型的配置，多角度地進行擬合分布曲線與IWRAP MKII運行結果的影響分析，讓本文的論點更具普適性，也更好地完善IWRAP MKII進行風險評估的適用性。