不同約束滑道形狀對多邊形效應的影響
王國晉,梁艷書,洪 林,錢蘭珠
(1.天津商業大學 機械工程學院,天津 300134;2.天津福臻工業裝備有限公司,天津 300350)
0 前言
鏈傳動的多邊形效應會對鏈條的工作性能產生非常嚴重的影響,特別是對大節距的輸送鏈[1-2]。文獻[3]對滑道約束型輸送鏈做出了靜態和動態理論的分析,建立了常規輸送鏈數學模型,并計算出所需的動態參數。文獻[4]提出了三種降低套筒滾子鏈傳動多邊形效應的常用方法,但本文中并不能夠用到。本文是采用改變滑道形狀的方法來比較多邊形效應的強弱的,通過對不同形狀的滑道進行分析,得出所需的參數,從而明確所提方案的優缺點。通過對比分析,驗證所構建的不同形狀的滑道約束型輸送鏈是否能夠減小其多邊形效應。
1 滑道約束型模型
常規鏈條模型如圖1所示。為了簡化后續計算,使右側半個圓周上正好可以放置三個鏈節[5]。從右側主動輪開始按順時針順序給銷軸取統一編號P1~P18,把P17作為自由銷軸,每兩個鏈節之間的長度p=150,兩側鏈輪的半徑r=150,左右兩鏈輪中心距為D=900,初始時P17的位置在預定滑道上。

圖1 常規輸送鏈模型
在現實使用中鏈條會出現受空間約束等特殊情況,所以提出兩種解決方案,將上下邊直線型滑道設計成向外凸出的圓弧型和向內凹進的圓弧型兩種,稱其為凸弧型輸送鏈和凹弧形輸送鏈兩種,如圖2和圖3所示。其中凸弧型左右鏈輪的中心距為886,上下滑道均為半徑2000的圓弧;凹弧型左右鏈輪的中心距為874,上下滑道均為半徑900的圓弧。初始時圖2和圖3中的P17均偏離了預定滑道。α1表示銷軸P1與主動鏈輪圓心連線和軸正半軸之間的夾角,同樣的αn表示銷軸Pn與靠近鏈輪連線和軸正半軸之間的夾角。假設右側輪的角速度大小ω=π。因為三種模型中除了自由銷軸外,其余銷軸均已被滑道所約束,所以微小的中心距變化所產生的誤差忽略不計。并且為了方便計算,本文僅分析在順時針轉動下的情況。
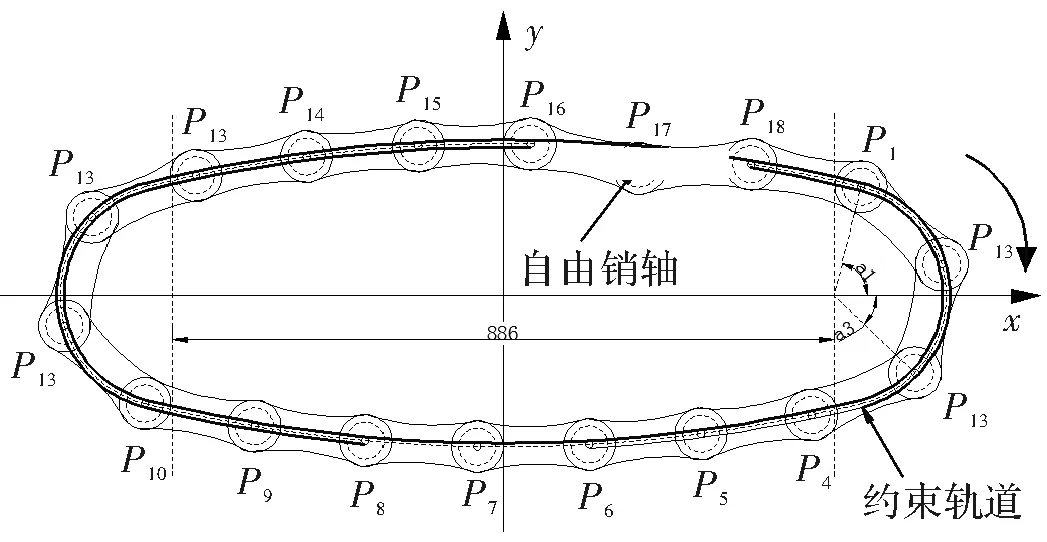
圖2 凸弧型輸送鏈模型
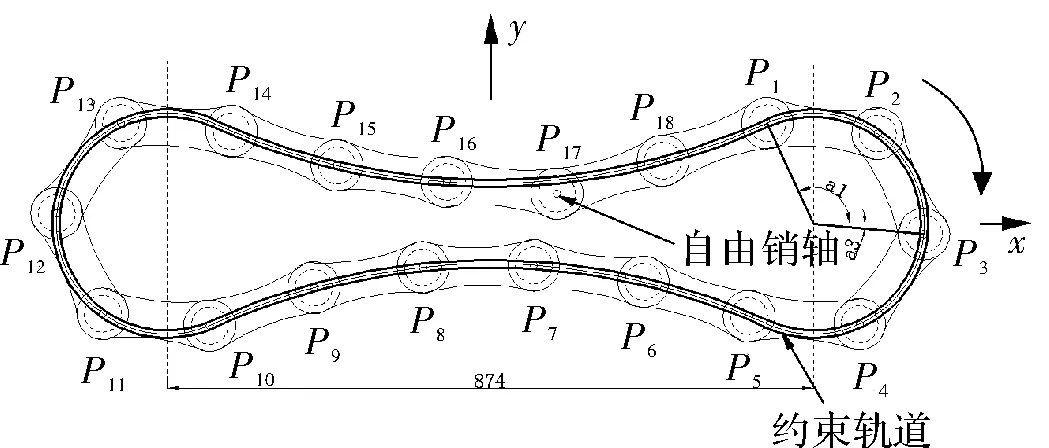
圖3 凹弧型輸送鏈模型
2 多邊形效應的表示方法
根據文獻[3]中的方法,使用Matlab軟件算出P17運行一周所經過的位置坐標,然后采用描點法獲得在靜態下的軌跡。在運動過程中,銷軸在左右兩個過渡區域會存在較大的多邊形效應,銷軸在速度上會有較大的差別。但是,因為除了P17外全都被滑道約束,所以由于不同的速度所產生的位移差就會全部表現在P17上。
為了表示多邊形效應的強弱,把左右過渡位置的銷軸在一個周期內的位移變化表示出來,位移變化越大則表明P17的振動越劇烈,即多邊形效應越強烈。以滑道的上半部分為研究對象,常規輸送鏈模型的運動分析圖如圖4所示。

圖4 常規輸送鏈運動分析

圖5 凸弧型輸送鏈運動分析
圖4中v1、v2為P1、P13的有效速度;vr1、vr2為P1、P13的真實速度;s1、s2為P1、P13的位移。可推導出v1和s1的計算公式為

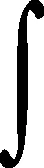
在一個周期內,和均有可能處于過渡區域,所以

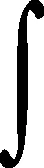
位移差為
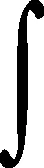
(1)
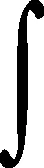
(2)
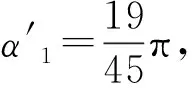
凹弧型輸送鏈運動分析如圖6所示,位移差為
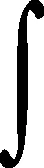
(3)
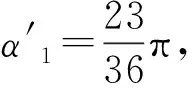

圖6 凹弧型輸送鏈運動分析
3 多邊形效應仿真
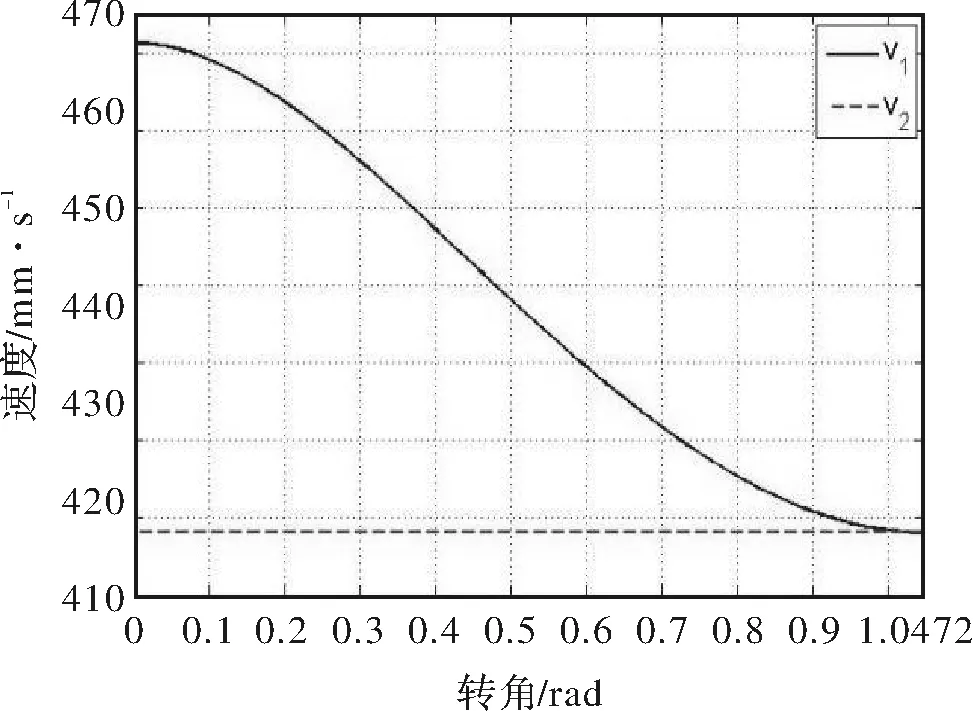
圖7 常規輸送鏈過渡區銷軸速度
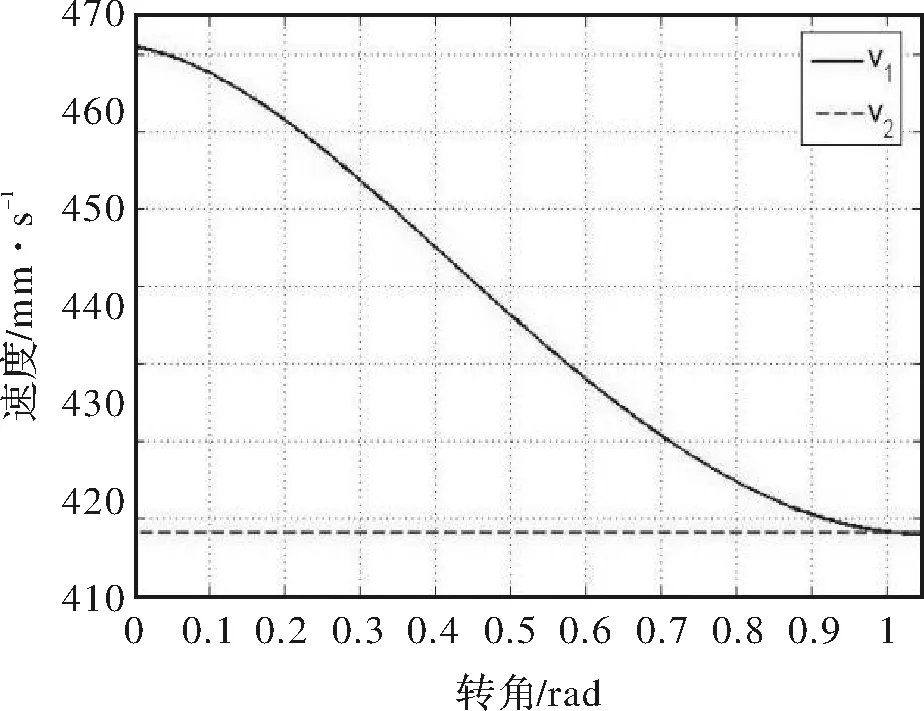
圖8 凸弧型輸送鏈過渡區銷軸速度
式(1)、 (2)和(3)是對兩個銷軸的速度積分作差而得到的位移差。由積分原理可知,將一個周期內時間段分割成有限的區間,用每個微小時間段內的某一時刻的速度來代替該時間段內的速度,然后將各段位移相加即得總位移,同一模型中兩不同銷軸的總位移作差即得總位移差。分割的區間越小,所得結果越準確。使用Matlab軟件得到的3種模型的總位移差如圖10所示。
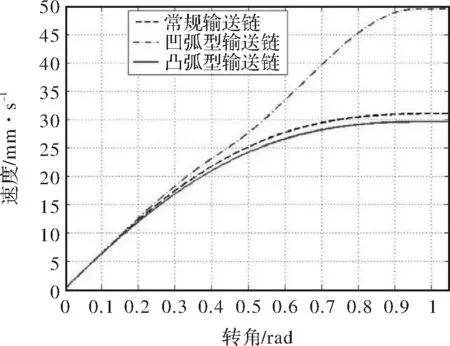
圖10 輸送鏈過渡區銷軸的總位移差
4 結論
對不同模型進行仿真分析比較多邊形效應的強弱,結果表明,相對于常規輸送鏈來說,凸弧形輸送鏈兩側銷軸的總位移差變小,可以減少鏈傳動的多邊形效應;凹弧形輸送鏈的總位移差變大很多,會使多邊形效應愈發明顯。在設計滑道約束型模型時,可以將直線滑道通過圓弧型滑道代替,圓弧滑道應使用凸弧型滑道來適當減小鏈傳動中的多邊形效應。

