永磁同步電機架懸直驅機構與驅動軸的干涉分析*
羅湘萍 徐 旻 田師嶠 張文超
(同濟大學鐵道與城市軌道交通研究院,201804,上海//第一作者,副教授)
0 引言
傳統轉向架的驅動電機選用異步交流電機,但異步交流電機的輸出特性無法滿足輪對低轉速、高轉矩的特點,需通過傳動齒輪加以調整,從而引發驅動裝置重量增加、齒輪傳動噪聲和能量損耗等一系列問題。
永磁同步電機直接驅動型轉向架舍棄了傳統轉向架上電機和輪對之間的傳動部件,直接將電機輸出的力矩傳遞給車輪或車軸[1]。相對于傳統的齒輪傳動轉向架,動力驅動系統更加簡單,重量更輕,可取消變速箱,減少效率損失,降低維護量和傳動噪音。同時,永磁同步電機具有功率密度大、低速輸出轉矩大、效率高等優點,因此將會逐步替代傳統異步交流電機,進而實現傳動系統的升級。
永磁同步電機有多種懸掛模式,按照直驅技術模式可分為永磁同步電機架懸直驅和永磁同步電機軸懸直驅,前者采用獨立空心軸作為電機轉子,電機懸掛于構架,車軸與轉子空心軸間采用彈性連接,其結構圖如圖1所示[2];后者采用車軸直接作為電機轉子的一部分,電機直接懸掛于車軸,其結構圖如圖2所示[3]。目前,對于中低速的軌道車輛,國外主要采用軸懸直驅模式。而對于較高速的軌道車輛,多采用架懸直驅模式。本文的研究對象為適用于城市軌道交通系統的準高速轉向架永磁同步電機架懸直驅結構。
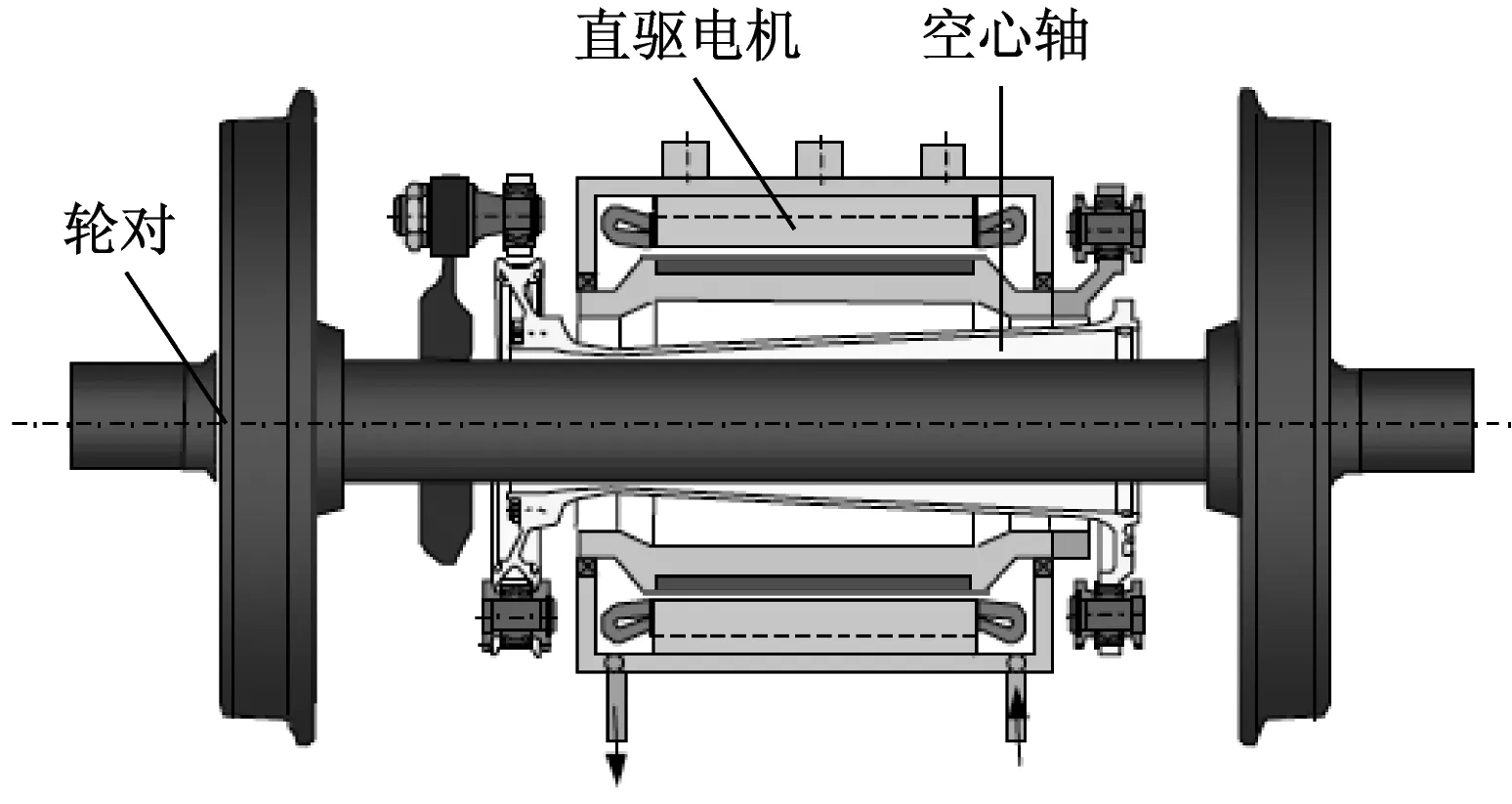
圖1 永磁同步電機架懸直驅結構圖
永磁同步電機架懸直驅技術,要求輪對與電機空心軸間留有一定間隙,來適應輪對與空心軸之間的動態變位。對于城市軌道交通車輛,此動態變位主要來自空重車變化下的一系彈簧垂向靜撓度改變量,軌道非線性病害沖擊,以及軌道隨機不平順激勵下的輪對和空心軸間動態位移。因此,永磁同步電機架懸直驅結構設計面臨如下技術難點:如何實現永磁同步直驅電機和車軸的匹配,并使之在軌縫、道岔或軌道病害等非線性沖擊以及軌道隨機激勵下不互相干涉。
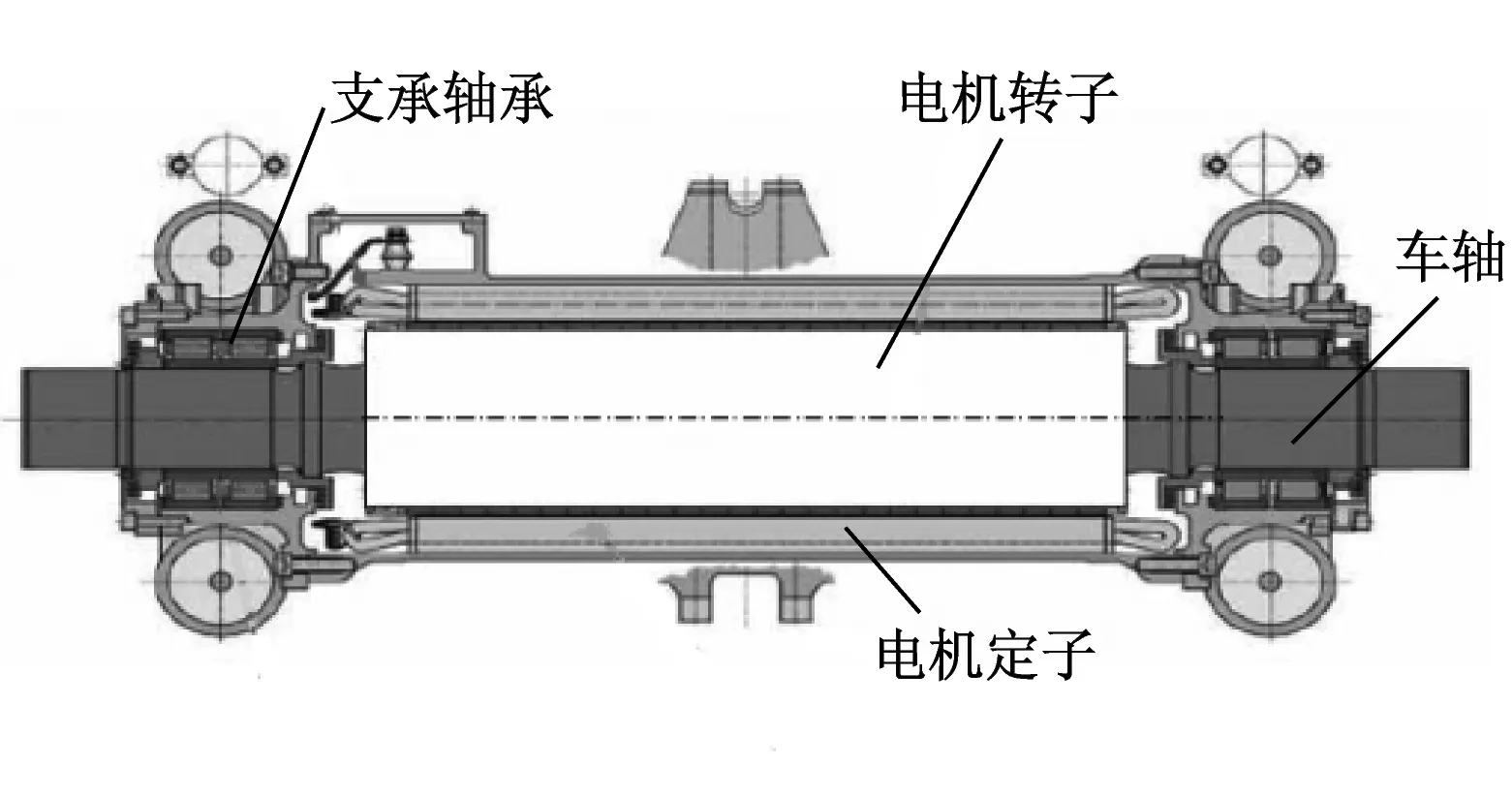
圖2 永磁同步電機軸懸直驅結構圖
為解決上述技術難點,分別建立永磁直驅柔性構架有限元瞬態響應分析模型及整車動力學模型,并提出架懸直驅結構與驅動軸間動態間隙的干涉評判指標,以此作為間隙大小設定的依據。
1 干涉性評判準則
圖3為空心軸與車軸、電機外殼間隙示意圖。圖3中,Gd為空心軸與車軸以及空心軸與電機下部垂向間隙設計值,Gu為空心軸與車軸以及空心軸與電機上部垂向間隙設計值。
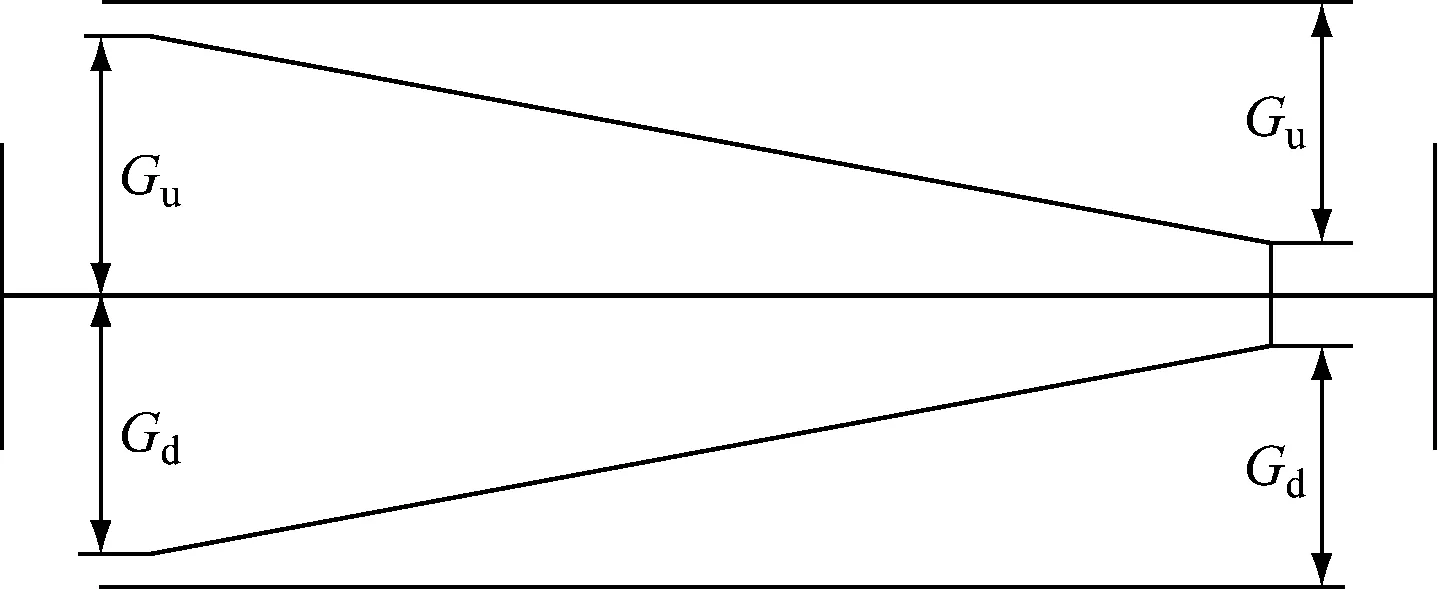
圖3 空心軸與車軸、電機外殼間隙示意圖
在下述兩種工況下,若Gd、Gu分別滿足式(1)、(2)的條件,則說明上述間隙值設計合理。
AW0(空載)工況:Gd≥Zi+Zr+S
(1)
AW3(超載)工況:Gu≥Zs+Zi+Zr+S
(2)
式中:
Zs——空重車一系彈簧垂向靜撓度變化值;
Zi——非線性沖擊下垂向動態間隙變化值;
Zr——軌道隨機激勵下垂向動態間隙變化值;
S——安全余量。
由式(1)可知,下部垂向間隙值未考慮空重車的變化量,其原因為城市軌道交通車輛存在的空重車變化,致使一系撓度變化較大。故為充分利用有限的間隙空間,采用驅動軸和空心軸內間隙不對稱分布設計:AW0工況下,上部間隙較大,下部間隙較小,此時僅需確保驅動軸與驅動機構下部不干涉;AW3工況下,因空重車變化,轉向架構架下移,導致驅動機構下移,故此時上部間隙變小,下部間隙變大,這種狀態下僅需確保驅動軸與驅動機構上部不干涉。
2 非線性瞬態響應分析
2.1 非線性有限元沖擊模型的建立
轉向架運行在軌道線路上時,軌道病害會造成輪軌沖擊,此沖擊力會導致電機與空心軸、空心軸與車軸間垂向動態位移發生變化。這是一個強烈非線性的沖擊過程[4-7],因此需要建立完整的永磁架懸直驅轉向架的有限元模型對其進行分析,圖4所示為轉向架-軌道耦合系統FEA(有限元分析)模型。

圖4 轉向架-軌道耦合系統FEA模型圖
2.2 非線性沖擊計算工況
在上述模型中,車輛轉向架運行速度為140 km/h。非線性沖擊子工況如表1所示。由表1中的5種子工況可排列出30個計算工況。例如,計算工況1:處于AW0狀態,左軌軌縫錯牙(前矮后高),右軌無病害;計算工況30:處于AW3狀態,左軌存在低接頭,右軌軌縫錯牙(前高后矮)。

表1 非線性沖擊子工況
2.3 非線性沖擊工況計算結果
非線性沖擊工況均以空心軸與車軸/電機殼體垂向相對動態位移的最大值為結果,其計算結果如表2所示。圖5所示為工況29和工況30下的空心軸與車軸和電機殼體垂向相對動態位移隨時間變化曲線圖。
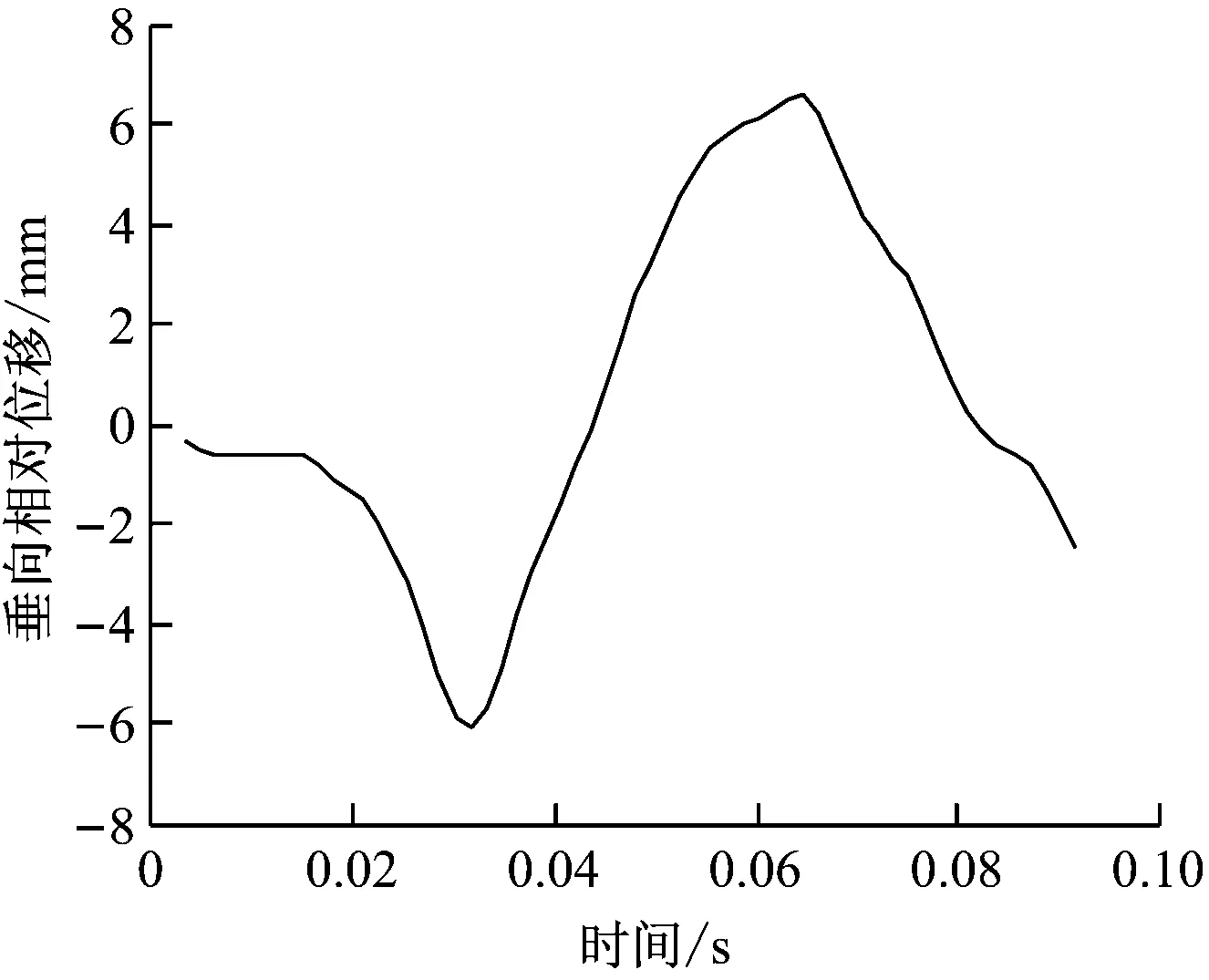
a) 工況29
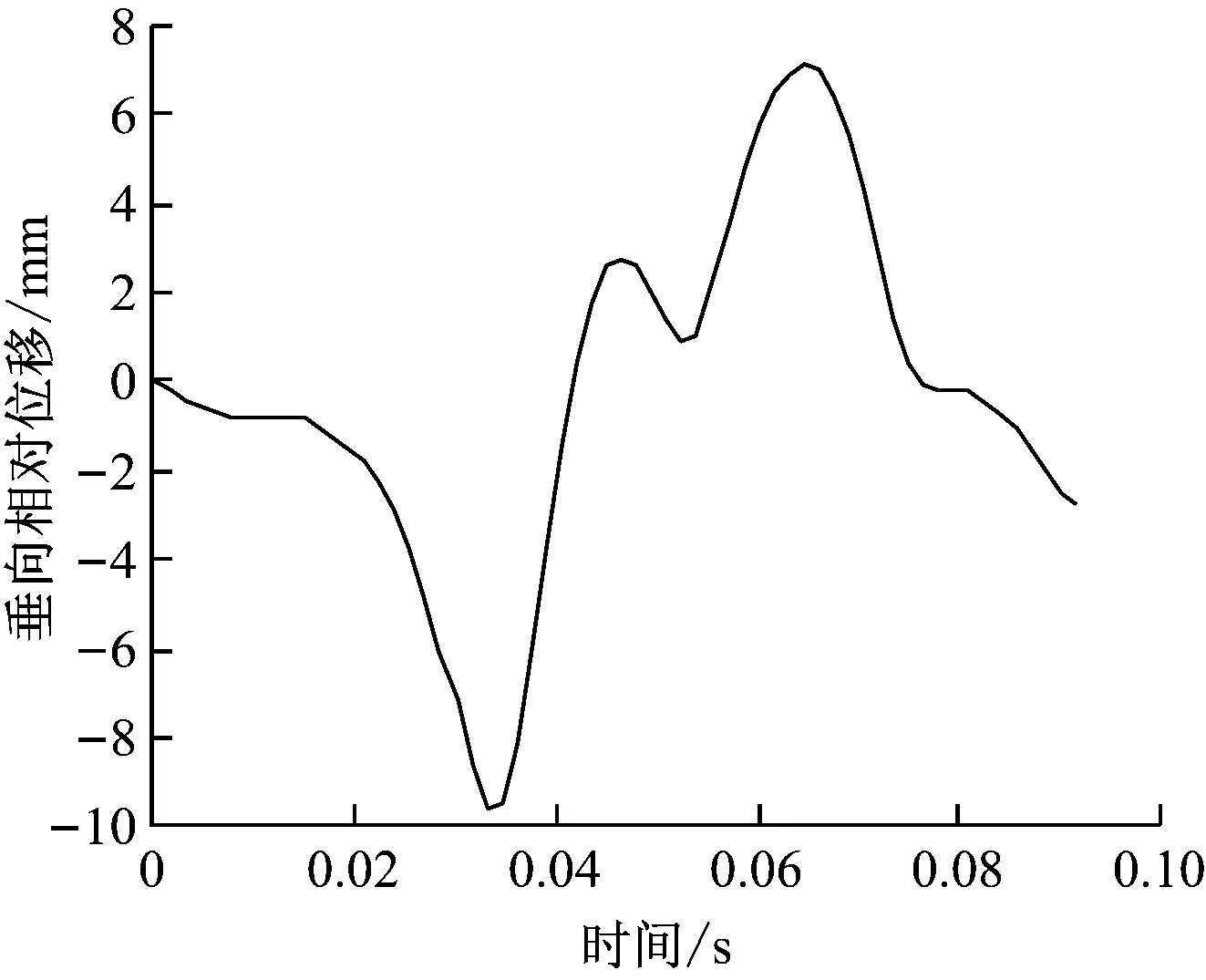
b) 工況30
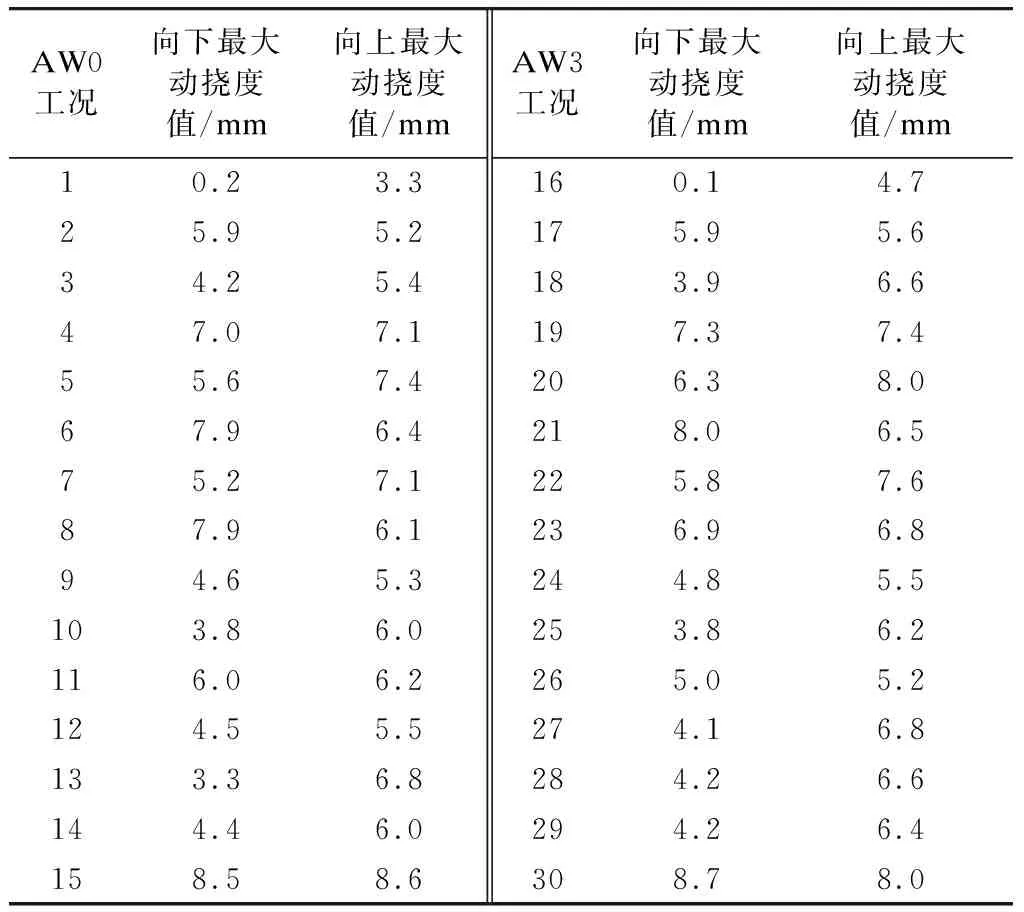
AW0工況向下最大動撓度值/mm向上最大動撓度值/mmAW3工況向下最大動撓度值/mm向上最大動撓度值/mm10.23.3160.14.725.95.2175.95.634.25.4183.96.647.07.1197.37.455.67.4206.38.067.96.4218.06.575.27.1225.87.687.96.1236.96.894.65.3244.85.5103.86.0253.86.2116.06.2265.05.2124.55.5274.16.8133.36.8284.26.6144.46.0294.26.4158.58.6308.78.0
AW0工況下,輪對與空心軸間下間隙小,故此時應考察各沖擊工況的向下最大動撓度值;AW3工況下,輪對與空心軸間上間隙小,故應考察各沖擊工況的向上最大動撓度值。
由表2可知:AW0工況下,向下最大動撓度值為8.5 mm;AW3工況下,向上最大動撓度值為8.0 mm,兩者較為接近。因為由軌道病害引起的輪軌垂向沖擊力主要由簧下質量決定,故由沖擊力引起的位移變化與車輛狀態AW0/AW3關系不大。
3 隨機響應動力學分析
利用Simpack建立配備永磁同步電機架懸直驅轉向架的整車動力學模型,分析計算時,加入軌道不平順的影響,并分別考慮直線軌道與曲線軌道兩種計算工況。
隨機響應動力學分析以電機與車軸的垂向相對動態位移為輸出結果,并取統計學中的3倍標準差,即3σ作為邊界值,各工況計算結果匯總如表3~4所示。
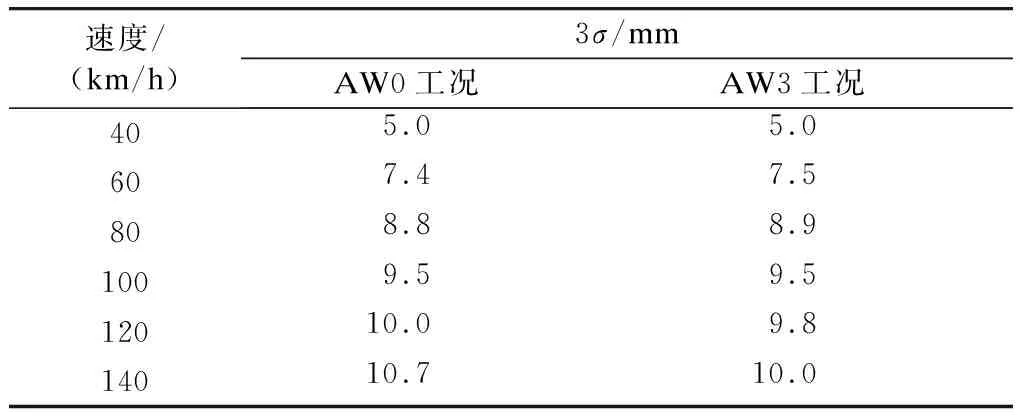
表3 直線軌道工況下的計算結果
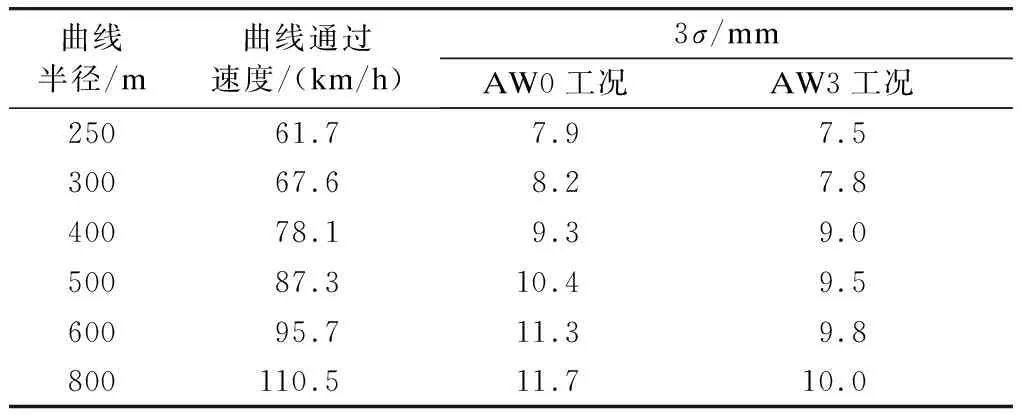
表4 曲線軌道工況下的計算結果
由表3~4可知:垂向動態相對位移隨著車輛運行速度的增加而增大;曲線軌道工況下,線路扭曲引起電機與車軸間存在側滾偏角,此角度在驅動機構與車軸間附加了一定的垂向位移,故相同速度等級下,曲線軌道工況的動態相對位移值較大。上述各工況下3σ最大值為11.7 mm。
4 干涉性評判
由上述非線性瞬態響應分析及動力學仿真結果可知,車輛在140 km/h的運行速度范圍內,非線性沖擊動態間隙向上最大變化值Zi為8.0 mm,向下最大變化值Zi為8.5 mm,隨機響應動態間隙最大變化值Zr為11.7 mm。空重車一系靜撓度變化Zs可由空重車載重變化及一系垂向剛度計算得到,其值為21.2 mm。
由干涉性評判標準可知,直驅機構與驅動軸上、下垂向間隙設計值Gu、Gd應滿足:
Gd=19.7+S
(3)
Gu=41.4+S
(4)
考慮一定的安全余量,并圓整上述數據可得到:驅動機構中輪對與內空心軸、內空心軸與電機垂向上空隙設計值Gd定為50 mm,垂向下空隙設計值Gu定為30 mm,以此保證車輛運行過程中直驅機構與驅動軸不發生干涉。
5 結語
本文基于非線性有限元沖擊模型、整車動力學模型,分析了各工況下驅動機構與驅動軸間垂向動態相對位移的變化情況,完成了永磁同步電機架懸直驅機構與驅動軸的動態匹配與間隙設計。驅動機構中輪對與內空心軸、內空心軸與電機垂向上空隙設計值Gd定為50 mm,垂向下空隙設計值Gu定為30 mm,以此確保轉向架運行過程中驅動機構與驅動軸不發生干涉,保證轉向架的運行安全。本文研究結論可為永磁架懸直驅機構的工程化運用提供參考。

