高動態環境下載波頻率的精確估計算法
金 磊
中國西南電子技術研究所,成都 610036
當飛機、火箭和導彈等載體作大機動運動時,接收信號的載波頻率會產生極大的多普勒頻移和多普勒變化率[1],而當載體處于障礙遮擋、多徑嚴重和信號干擾等環境時,信號功率由于受到各種信道損耗而嚴重衰減[2],因此,高動態、弱信號等復雜因素在很大程度上制約著衛星導航、航天測控及雷達探測等通信產品的應用范圍。隨著眾多軍民用通信產品對其性能需求的不斷提升,如何在高動態、弱信號等復雜環境下實現載波頻率的精確快速估計已成為研究焦點,目前國內外廣大科研學者和機構對其進行了持久深入的研究。
國外學者從上世紀已開始研究并給出多種解決辦法,Hurd W等采用最大似然估計(MLE)算法得到多普勒頻移估計值,適用于高動態環境,具有較高精度[3];Kumar R等提出了自適應最小均方誤差(ALS)估計算法,測量精度高,能夠適應快速變化的頻率[4];Jack M等采用信號包絡的平方偏差實時估計多普勒頻移,此算法的復雜度較高但可適用于低信噪比環境[5]。
國內學者開展研究較晚但也取得了大量研究成果,楊昂研究了高動態環境下各種經典的多普勒頻移估計算法,并在此基礎上提出了改進的多普勒頻移估計算法[6];黃富彪等結合類Rife頻率修正算法提出了適用于數字方法實現的衛星信號載波頻率高精度估計算法[7];易輝等通過非線性變換將BPSK信號轉化點頻信號并采用相位差校正法提高了估計精度[8];鄭紀民等對非線性變換后的信號進行正交下變頻和2級DFT,精確估計了MPSK信號的載波頻率[9]。
上述各研究均只對多普勒頻移進行了高精度快速估計,并未考慮復雜環境下的多普勒變化率,且難以在動態范圍、信號強弱、搜索時間、測頻精度和資源消耗等因素之間達到均衡,為了克服上述現存缺陷,本文提出了一種改進的載波頻率估計算法。該算法在快速傅里葉變換前對降采樣數據進行載波頻率的雙重補償,實現多普勒頻移、多普勒變化率的雙重估計;在不同的測頻狀態,根據信號調制類型進行模式識別與控制完成載波恢復,可提高載波頻率的搜索范圍和測量精度;在粗測頻、精測頻狀態對第一級降采樣數據頻率預補償后進行第二級降采樣處理,可適當縮短測頻狀態的搜索時間。
1 算法原理
改進的載波頻率估計算法的具體原理結構如圖1所示,其主要由主控單元(1)、第一級降采樣(2)、頻率補償(4)、第二級降采樣(5)、模式識別與控制(7)、快速傅里葉變換(8)和峰值搜索頻率解算(9)等單元組成。

圖1 改進的載波頻率估計算法原理結構圖
下面分別對該算法原理結構各功能模塊的工作原理進行詳細說明[10-11]:
1.1 主控單元
主控單元控制整個測頻狀態,根據輸入信號的測頻范圍和調制類型確定各測頻狀態中降采樣頻率、存儲容量、頻率補償、模式識別、峰值搜索和頻率解算等狀態參數,控制其他功能模塊的數據傳輸,通過資源復用實現通用化。
1.2 降采樣單元
兩級降采樣單元均采用ID積分濾波器結構,主要包括DDS、積分清零和數據截位等3個部分,根據主控單元的測頻狀態確定積分頻率控制字,由DDS產生清零脈沖,對輸入數據進行積分清零操作以完成ID積分濾波,最后將積分濾波數據有效截位輸出至存儲單元。
1.3 頻率補償單元
頻率補償單元根據每個頻率細分槽的多普勒頻移fdopl、多普勒變化率frate得到多普勒頻移控制字Kdopl和多普勒變化率控制字Krate,分別通過地址映射、查表生成2路本地載波,經過復乘運算后得到本地復合載波,然后將采樣數據和本地復合載波進行復乘運算,對采樣數據完成多普勒頻移、多普勒變化率的雙重補償,其具體結構如圖2所示。

圖2 頻率補償單元結構圖
圖2中多普勒頻移控制字Kdopl、多普勒變化率控制字Krate可由下式計算得到,
其中,fs是降采樣數據的采樣頻率。
1.4 模式識別與控制單元
模式識別與控制單元根據主控單元的測頻狀態和輸入信號的調制類型確定控制狀態,在初測頻狀態,將輸入信號統一劃分為單頻模式進行處理;在粗測頻、精測頻狀態,根據輸入信號的調制類型完成信號的載波恢復,其中將BPSK信號劃分為二倍頻模式,將QPSK,SQPSK和UQPSK信號等劃分為四倍頻模式。
二倍頻模式為了恢復BPSK信號被抑制的載波,在進行快速傅里葉變換之前需對BPSK信號進行平方運算完成載波恢復,而平方運算帶來了處理信號的信噪比惡化[12],其惡化損失可由下式計算得到
其中,SNRi為輸入信噪比。
同理,四倍頻模式為了恢復QPSK,SQPSK以及UQPSK信號等被抑制的載波,需對QPSK,SQPSK和UQPSK信號等進行四次方運算完成載波恢復,而四次方運算帶來了處理信號更嚴重的的信噪比惡化,通過仿真可得到其惡化損失。
綜上分析,二倍頻模式和四倍頻模式帶來的處理信號信噪比惡化損失曲線如圖3所示

圖3 處理信號信噪比惡化損失曲線圖
1.5 峰值搜索與頻率解算單元
峰值搜索與頻率解算單元將快速傅里葉變換輸出的處理結果經過非相干積分累加后進行峰值判決,單頻模式采用頻譜重心法,其余模式均采用頻譜比較法,得到每個頻率槽的峰值,然后對當前測頻狀態所有頻率槽進行峰值比較,找到最大峰值以及其所對應的頻率槽,完成當前測頻狀態采樣數據的頻率搜索,最后計算并輸出所得的多普勒頻移、多普勒變化率。
2 流程控制
主控單元將整個測頻過程分為初測頻、粗測頻、精測頻等3個狀態,根據輸入信號的測頻范圍、調制類型等確定各測頻狀態的狀態參數和控制各功能模塊間的數據傳輸,具體流程控制如圖4所示,圖中詳細說明了各測頻狀態的工作原理。

圖4 改進的載波頻率估計算法流程控制圖
2.1 初測頻狀態
初測頻狀態根據測頻范圍對輸入信號完成第一級降采樣處理,對第一級降采樣數據進行多普勒變化率的頻率補償后以單頻模式進行測頻,得到粗略的多普勒頻移測量值。
設最大多普勒頻移為fdopl_max,最大多普勒變化率為frate_max,系統工作時鐘為fclk,則第一級降采樣頻率為
fs≥4fdopl_max
為了檢測輸入信號被抑制的載波,第一級降采樣數據量為Nfull,則第一級降采樣時間為
ts=Nfull/fs
快速傅里葉變換測頻點數為COH,則多普勒頻移、多普勒變化率的測量精度為
初測頻狀態對第一級降采樣數據以單頻模式進行測頻,測頻精度較差,則頻率補償的多普勒變化率步長可為frate_max≤4frate_res1、其載波頻率搜索輪次分別為
slotfull≥2frate_max/frate_step1
則初測頻狀態的搜索時間為
tfull=ts+Nfull/fclk×slotfull
2.2 粗測頻狀態
粗測頻狀態采用初測頻狀態得到的多普勒頻移測量值對第一級降采樣數據完成頻率預補償處理后進行第二級降采樣處理,對第二級降采樣數據完成多普勒頻移、多普勒變化率的雙重頻率補償后進行輸入信號的模式識別,得到較精確的多普勒頻移測量值和粗略的多普勒變化率測量值。
粗測頻狀態第二級降采樣的ID積分濾波點數為ID2coarse,則第二級降采樣數據量為,
Ncoarse=Nfull/ID2coarse
則其第二級采樣時間為
tid 2=Nfull/fclk
粗測頻狀態的多普勒頻移、多普勒變化率的測量精度為
式中,K為模式識別的控制指數,二倍頻模式時為2,四倍頻模式時為4。
粗測頻狀態根據輸入信號的調制類型確定模式識別的控制狀態,其測頻精度較好,則頻率補償的多普勒變化率步長可為frate_step2≤2frate_res2,其載波頻率搜索輪次為
slotcoarse≥4frate_step1/frate_step2
則粗測頻狀態的搜索時間為
tcoarse=tid2+Ncoarse/fclk×slotcoarse
2.3 精測頻狀態
精測頻狀態采用粗測頻狀態得到的載波頻率測量值對第一級降采樣數據完成較精確的頻率預補償處理,并重復粗測頻狀態的操作流程,從而得到更精確的多普勒頻移和多普勒變化率測量值。
精測頻狀態第二級降采樣的ID積分濾波點數為ID2fine(ID2fine>ID2coarse),其測頻狀態的操作流程同上所述,可得精測頻狀態的第二級降采樣數據量為Nfine、多普勒頻移測量精度fdopl_res3、多普勒變化率測量精度frate_res3及多普勒變化率步長frate_step3,頻率預補償的多普勒變化率為概略測量值,需進一步提高其測量精度,則其載波頻率搜索輪次為
slotfine≥2frate_step2/frate_step3
則精測頻狀態的搜索時間為
tfine=tid 2+Nfine/fclk×slotfine

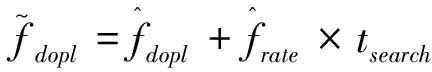
3 試驗與分析
為檢驗該算法的測頻性能,采用某FPGA+DSP平臺進行測頻試驗,其參數設置如下:系統工作時鐘fclk為120MHz,數據調制速率Rb為10kbps,多普勒頻移范圍fdopl_max為±250kHz,多普勒變化范圍frate_max為±25kHz/s。
3.1 測頻精度
若接收信號為BPSK信號時,在初測頻狀態,第一級降頻率采樣為fs=1000kHz,為了檢測接收信號中已完全淹沒在背景噪聲的載波頻率,需延長積分時間以增加積分增益,則采樣時間ts為0.256s,FFT測頻點數COH選取2048,其載波頻率搜索輪次slotfull為30;在粗測頻狀態,第二級降采樣的ID積分濾波點數ID2coarse為4,其載波頻率搜索輪次slotcoarse為100;在精測頻狀態,第二級降采樣的ID積分濾波點數ID2fine為16,其載波頻率搜索輪次slotfine為40;模式識別與控制單元在初測頻狀態采用單頻模式,在粗測頻、精測頻狀態采用二倍頻模式。則根據上述理論分析可知整個測頻過程的搜索時間、多普勒頻移精度、多普勒變化率精度分別約為0.386s、±10.0Hz和±30Hz/s。
若接收信號為QPSK信號時,初測頻、粗測頻狀態流程同上,在精測頻狀態,第二級降采樣的ID積分濾波點數ID2fine為8,其載波頻率搜索輪次slotfine為60;模式識別與控制單元在初測頻狀態采用單頻模式,在粗測頻、精測頻狀態采用四倍頻模式。則根據上述理論分析可知整個測頻過程的搜索時間、多普勒頻移精度及多普勒變化率精度分別約為0.397s、±10.0Hz和±30Hz/s。
3.2 檢測概率
根據參數設置,在不同頻率動態范圍、不同信噪比條件下對該算法的檢測概率Pd進行試驗分析,以多普勒頻移誤差Δfdopl≤20Hz、多普勒變化率誤差Δfrate≤50Hz/s為成功檢測條件,可得試驗結果如圖5~6所示。
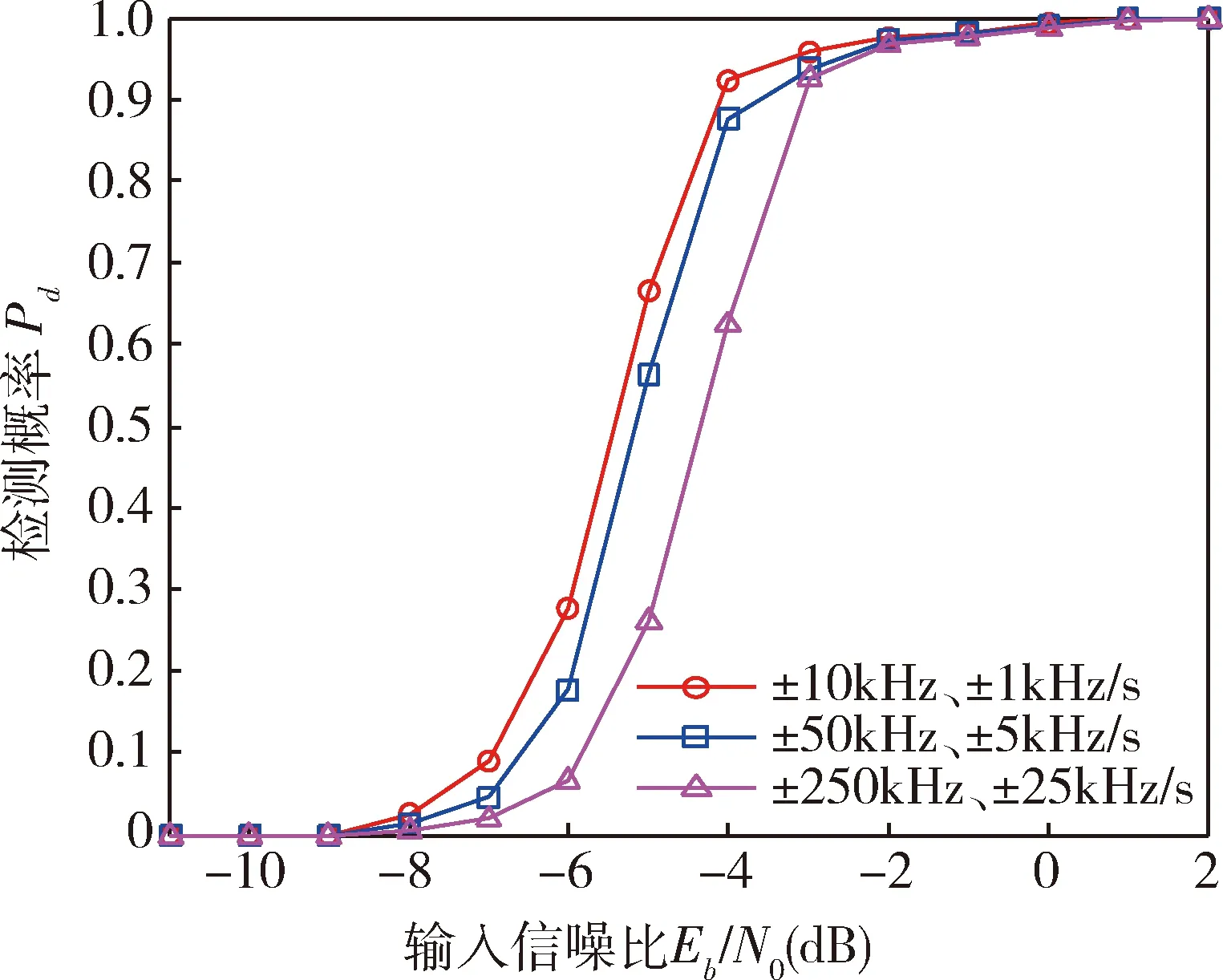
圖5 BPSK信號測頻試驗檢測概率圖

圖6 QPSK信號測頻試驗檢測概率圖
圖5為BPSK信號測頻試驗的檢測概率統計,當輸入信噪比Eb/N0≥-3.0dB時,該算法在不同頻率動態范圍的檢測概率Pd≥90%;圖6為QPSK信號測頻試驗的檢測概率統計,當輸入信噪比Eb/N0≥4.0dB時,該算法在不同頻率動態范圍的檢測概率Pd≥90%;當頻率動態逐漸增大時,相干積分的扇貝效應和FFT運算的柵欄效應讓輸出增益產生衰減,相應地降低檢測概率,但該算法在高動態環境下仍具有明顯的性能優勢。
4 結論
研究了高動態環境下載波頻率的精確估計問題,在總結國內外研究現狀的基礎上,提出了一種改進的載波頻率精確估計算法,詳細說明該算法的原理結構和流程控制,實現了多普勒頻移、多普勒變化率的同時精確估計,可適應BPSK、QPSK、SQPSK和UQPSK等多種不同調制類型和調制速率的輸入信號,并完成該算法在高動態低信噪比條件下的試驗實驗。通過試驗分析可以看出,該算法具有更大的搜索范圍、更高的估計精度及更好的測量性能,在復雜環境下有更明顯的應用優勢。

