基于混合遺傳算法的鐵路物流中心布局研究

劉姣姣

（中國鐵路設計集團有限公司 線站院，天津 300142）

0 引言

傳統鐵路貨場向現代鐵路物流中心（園區）轉型是我國鐵路貨運組織改革的一項重要任務，物流中心除具備原有鐵路貨運站功能外，還將融入現代物流服務，吸引相關企業入駐，使傳統的鐵路貨運功能得到增值。

傳統的鐵路物流中心包括貨物倉儲區、包裝區、加工區、配送區、商貿業務區、公鐵聯運區、物流金融區、電子交易區、集裝箱轉運區等不同功能區。將它們按照一定的優化準則組合在一起，充分發揮各區域的功能屬于一種布局問題[1-2]。

布局問題是NP-hard問題，由于布局問題的復雜性，在有限的時間內難以獲得問題的精確解[3-4]，所以絕大部分解決布局問題的算法是啟發式的，在這些啟發式算法中，遺傳算法以其高效性、并行性和較好的魯棒性在布局問題中得到了較為廣泛的應用[5-6]。在國內，一部分研究者已將遺傳算法應用于鋼鐵物流中心的內部規劃[7-8]和鐵路物流中心的布局研究[9-10]。

物流中心的最優布局依賴于優化模型的合理性和優化算法的高效性。傳統的模型多以矩形為物流中心邊界，并采用傳統的遺傳算法進行求解，假設其矩形邊界缺乏對實際不規則邊界的適應性，而傳統遺傳算法通常因早熟而易陷入局部最優解。為解決上述問題，通過建立能夠考慮物流中心不規則邊界條件的優化模型，在傳統遺傳算法中引入模擬退火局部搜索機制，以增強算法的全局收斂性，從而獲得最優的、合理的物流中心布局。

1 鐵路物流中心最優布局數學模型

1.1 最優目標的原則及優化模型

物流中心布局規劃應當遵循以下原則[11]：①運輸成本最小化；②功能區之間的聯系最大化；③功能區之間不能重疊并保持一定的距離；④功能區應當在物流中心規劃范圍內。運輸成本最優模型計算公式為

式中：F1為運輸成本；dij為i到j的距離；gij為i到j運輸物品的重量。

功能區之間關系最大化模型計算公式為

式中：目標函數將功能區之間關系最大化模型轉換為最小化模型形式，F2為功能區之間的關系函數；V為功能區i與j的最大相鄰關聯度（取V= 4）；Rij為i與j的相互關系，分為物流關系mrij和非物流關系nrij，通過權重系數α和β加權組成；非物流關系由與業務流程、組織管理和環境安全的nrij1，nrij2，nrij3通過權重系數w1，w2，w3組成；bij為廣義距離相鄰度[7]。

為了適應物流中心土地的實際情況，增強優化目標的靈活性，建立了考慮不規則邊界情況的約束條件準則。根據功能區的特點，一般功能區均以矩形功能區為主，而園區土地邊界可以考慮任意的邊界形狀。功能區變量示意圖如圖1所示，對于一個功能區而言，中心坐標 （xi，yi）、長度Li、寬度Wi和角度αi可惟一確定該功能區的位置和形態，第k個角點的坐標計算公式為

式中：θi1—θi4分別為功能區4個角點相對于X坐標軸正方向的角度。

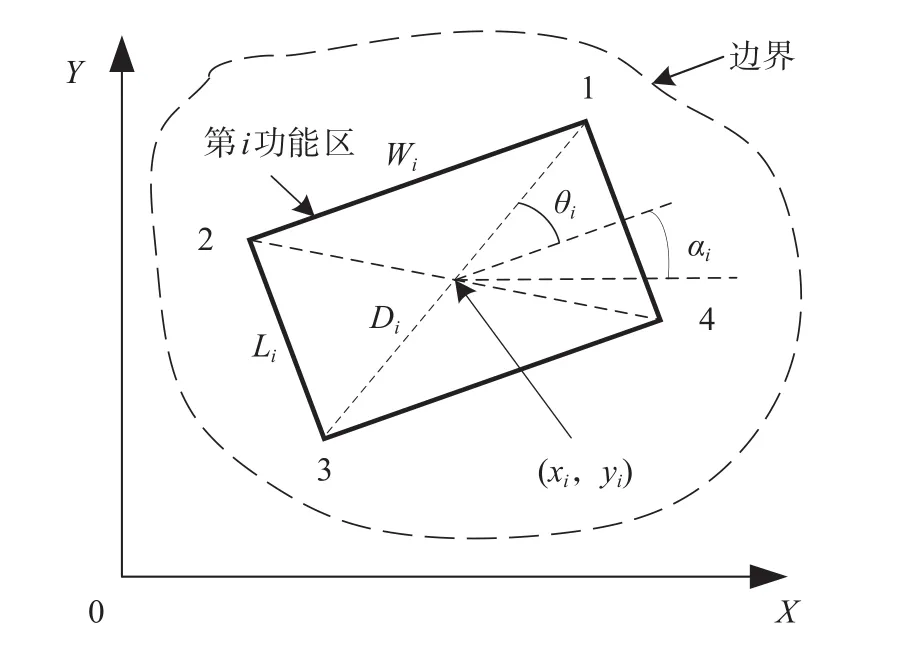
圖1 功能區變量示意圖Fig.1 Sketch map of functional area variables

1.2 約束條件

模型需滿足2個約束條件：①功能區之間不能重合；②功能區不得超出邊界，其中邊界通過連續坐標點表示。這2種約束條件可采用計算幾何的射線法或面積法[12]從檢驗功能區i與功能區j的點面相對關系，以及功能區i與物流中心邊界區域的點面關系予以判定。當滿足上述2個邊界條件時，罰函數置為0，否則，設置一個較大的罰數。此外，每個功能區的長度和寬度要保持一定的比例，即：λmin≤λi=Li/Wi180°≤λmax。按照歸一化原則并考慮各種權重可將2個子目標函數組合成一個單目標函數。

式中：μ1，μ2分別為 2 個子函數權重系數，μ1+μ2= 1；歸一化系數其中V含義同前，可取4；Np1，Np2，Np3分別為功能區相互重疊數目、功能區超出物流中心用地界的數目和功能區長寬比超出規定范圍的數目。

優化目標函數的優化變量為xi，yi，αi，Li，Wi。優化目標函數同時覆蓋了2個子優化目標，并同時考慮了邊界約束條件。此外，還能夠針對任意物流中心邊界形狀的情況進行優化。

1.3 算法設計

混合遺傳算法將傳統的遺傳算法與模擬退火算法結合，發揮遺傳算法泛化搜索和模擬退火算法局部精細化搜索的優點。為了避免Hamming懸崖問題[13]，采用格雷碼進行算法設計。

將模擬退火算法融入遺傳算法，以遺傳算法中的適應度比模擬退火算法中的內能，將執行遺傳操作之前的種群作為模擬退火算法的輸入解，對該輸入解進行遺傳操作產生新解（即遺傳算法的新個體），并利用Metropolis抽樣法則對新解進行抽樣。在算法搜索初期，解的分布范圍比較廣，且目標函數的曲面上分布較多局部峰谷，對適應度較低的解，接受概率比較大。在搜索后期，逐步逼近全局最優，接受適應度較低解的概率應當趨于0。

在整個算法過程中，遺傳算法的進化代數與模擬退火的溫度進程統一為一個循環控制參數，使得每次遺傳算法操作均發生在模擬退火算法的某一溫度下，具體算法如下。

（1）設置各項參數，隨機產生初始種群。

（2）評價初始種群的個體適應度，將高適應度的個體作為父代種群。

（3）父代種群根據設定的交叉概率和變異概率執行交叉和變異操作產生子代。

（4）根據進化代數，確定相應的模擬退火溫度，執行模擬退火局部搜索，保留優秀個體。

（5）檢驗結果是否收斂，若收斂則輸出最優解并結束搜索，否則轉（2）。

1.4 算法檢驗

通過搜索經典有解析解的Schaffer函數的最大值來檢驗所設計混合遺傳算法的有效性。該函數全局最大值為1 （x= 0，y= 0），在全局最高點附近有一圈局部次高點，其對應的值約為0.990 28，其函數表達式為

混合遺傳算法的控制參數設置如下：最大進化代數200，種群規模200，交叉概率0.7，變異概率0.05，初始溫度10 000。函數圖像如圖2所示，測試函數尋優收斂曲線如圖3所示，測試函數優化結果如表1所示。在圖3中，以解的變化曲線表示每一代群體中最優秀得個體，用均值表示每一代群體的總體情況，由于函數的多峰值性，搜索前期震蕩較大，在前75代左右解的收斂曲線呈階梯形上升，目標函數值由0.995跳到無限接近1的位置，同時均值收斂曲線斜率增大，收斂速度加快，與解的收斂曲線幾乎重合，快速穩定地收斂到全局最優解，說明該算法具有很強的全局搜索能力。

圖2 函數圖像Fig.2 Function images

圖3 測試函數尋優收斂曲線Fig.3 Test function optimization convergence curve

表1 測試函數優化結果Tab.1 Test function optimization results

2 實例分析

某鐵路物流中心規劃總占地1 200 000 m2，由于市政規劃道路的分割和地形條件的限制，可被用作物流中心的用地邊界通常是不規則的。物流中心包括倉儲區、保稅區、配送區、流通加工區、交易展示區、辦公生活區、集中停車區7大功能區。各功能區規劃用地面積如表2所示，各功能區之間日均物流量如表 3所示，各功能區之間綜合物流關系如表 4所示。

表2 各功能區規劃用地面積 m2Tab.2 Planning area of each functional area

表3 各功能區之間日均物流量 tTab.3 Daily average volume of flow between each functional area

表4 各功能區之間綜合物流關系Tab.4 Integrated logistics relationship among functional areas

通過優化模型以及混合遺傳算法的優化求解方法，所得到的最優物流中心總布置如圖 4所示。由圖 4中可知，物理中心布局中將停車場沿用地界的斜邊布置，這樣可以節省場地并滿足用地需求，同時距離關系緊密貨運量大的倉儲區、配送區和流通加工區較近，交易展示區和辦公生活服務區位于左下角，最大程度實現了物流中心的優化配置。

圖4 物流中心總布置圖Fig.4 General layout of logistics center

3 結論

針對不規則物流中心的優化目標函數，引入了局部搜索能力較強的模擬退火算法，形成了物流中心布局最優化的整套解決方案，并對某物流中心進行了布局的優化，主要結論如下。

（1）提出可以適應于不同邊界形狀物流中心用地的優化算法，同時在功能區的空間優化目標函數中引入了轉動自由度，以適應不規則邊界的功能區布局問題。

（2）將傳統遺傳算法與模擬退火算法相結合，增強優化方法的全局收斂性，保證了優化求解的精度。

（3）物流中心的最優布局取決于優化目標函數的合理性以及求解方法的高效性，所建立的目標函數能夠很好地考慮實際物流中心規劃中遇到的用地形狀問題，同時算法本身具備很強的全局搜索能力，因而有更廣泛的實用性。

（4）為物流中心的布局提供一種方法，為后續的物流中心設計提供一個理論的最優布局方案，在實際應用中，僅需要根據實際情況進行局部修改和調整即可形成最終的物流中心布局方案。