山區單懸臂廊橋結構抖振響應及等效風荷載

蘇 益 ，李明水 ，楊 陽 ，段青松

（1. 西南交通大學土木工程學院，四川 成都 610031；2. 西南交通大學風工程四川省重點實驗室，四川 成都610031）

抖振是紊流作用引起的結構隨機振動，以紊流中脈動部分引起的結構強迫振動為主，一般不會引起災難性破壞，但會導致結構的功能性障礙，且在任意風速下均可發生. 對于橋梁結構而言，過大的抖振會危及結構安全、影響行人及車輛舒適度、縮短部分構件疲勞壽命等. 隨著人們對橋梁風工程深入研究發現，風敏感的橋梁結構不僅限于大跨度橋梁，很多短、中跨橋梁結構也被歸為風敏感結構中，如某些人行橋梁等[1]. 近年來更有多座山區懸挑式觀景廊橋出現，諸如科羅拉多U型廊橋、重慶云陽廊橋、重慶萬盛廊橋等，且懸挑長度不斷增大. 目前山區橋梁抗風大都針對懸索橋及斜拉橋等大跨度橋梁[2-3]，此類懸挑式廊橋的抗風問題研究極少. 并且由于山區風環境的復雜性，尚無法利用規范獲得設計參數，需通過風洞試驗等手段進行研究.

山區地形復雜，局部風環境影響因素多，深入研究橋位風環境是山區橋梁抗風設計的前提[4-6]. 山區各類風場特性參數對結構三分力系數及抖振響應均有影響[7]. 文獻[8]中就風場參數的不確定性對風振響應的影響做過研究，并給出相應結論. 河南新鄉南太行關山一號拉索觀景廊橋建于海拔1 533 m懸崖邊緣，懸挑長度70 m，設計風速48 m/s. 本文以該廊橋結構為背景，針對各風場特性進行風洞試驗，根據試驗結果分析各參數對結構三分力及抖振響應的影響，并給出結構等效靜力風荷載，為山區風環境下類似長懸挑結構的抗風設計與研究提供參考.

1 試驗概況

1.1 試驗設備及模型

試驗在西南交通大學3號風洞中進行. 風洞試驗段截面尺寸22.5 m × 4.5 m，風速范圍1.0～16.5 m/s.試驗段底壁設有轉盤，可實現風向角的變換. 試驗采用5 kg、5分量天平測量懸挑底部的基底力，并用激光位移傳感器測量懸挑尖端的位移響應.

綜合考慮結構尺寸、地形特點，及阻塞率要求，在風洞中最大限度地還原了橋址處地形. 模型幾何縮尺比為1∶50. 模型主梁長1.4 m，最寬位置0.463 m，在風洞中的阻塞率小于5%，滿足試驗要求.

1.2 大氣邊界層模擬

試驗段配備由尖塔、擋板和粗糙元等組成的邊界層模擬裝置. 試驗設計了3種風場，并在2種風速下分別進行. 經測量，3種風場特性參數如表1所示.表中： Um為試驗風速； Uf為實際風速； Iu、 Iw分別為 u 、w方向紊流度； Lu、 Lw分別為 u 和 w 方向紊流積分尺度. 模擬風譜在橋梁抖振所依賴的折算頻率范圍內（ f ＞10-1）與von Kármán譜吻合良好，滿足抖振試驗要求.

表1 各類風場特性參數Tab.1 Characteristic parameters of wind fields

1.3 試驗工況

試驗共分兩部分，第1部分為剛性模型測力試驗，獲得結構靜力三分力系數；第2部分為通過擬彈性模型準確模擬結構動力特性，測量結構的抖振響應. 圖1為模型風洞試驗圖. 由圖1可知，廊橋周邊山體均為近似垂直于水平面的懸崖. 當結構處于0°風向角時，來流向廊橋受風面幾乎沒有山體遮擋；當結構處于180° 風向角時，順風向廊橋的受風面有部分山體遮擋，遮擋寬度約為橋長的1/4～1/3.

試驗風攻角及風向角示意圖如圖2所示，圖中：風攻角包含 - 3°、0°、 + 3°；三分力系數試驗包括0°～180° 范圍內風向角；抖振試驗包括全部角度；試驗在前述3種風場及2種風速下進行.

圖1 模型風洞試驗示意Fig.1 Schematic of model and wind tunnel test

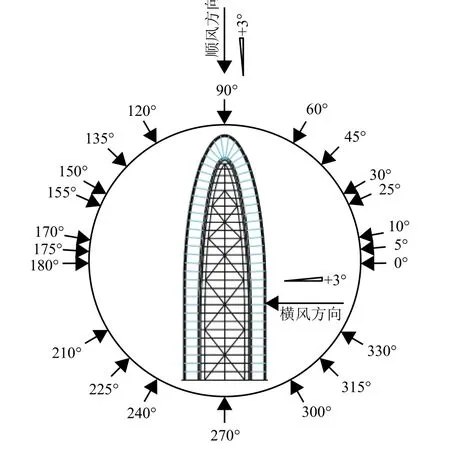
圖2 風洞試驗風向角及風攻角示意Fig.2 Diagram of wind direction and angle of attack

2 靜力三分力系數結果及分析

靜力三分力系數是表征各類結構斷面在平均風作用下受力大小的無量綱系數，反映了風對結構的定常氣動力作用. 根據試驗得到結構在體軸系下的靜力三分力系數，如圖3所示. 圖中： CV、 CH、CM分別為升力系數、阻力系數和扭矩系數； α 為風向角.

由圖3可知，隨著風攻角和風向角變化，場地模型對風場影響明顯，三分力系數變化較大. 3個風攻角各曲線隨風向角改變的變化趨勢大體相同，但系數值有明顯差別. 因地形不對稱等差異，0°～90° 和 90°～180° 的三分力系數未呈現對稱的結果，前者各系數值普遍高于后者.

由于山體地形的影響，從0°～180° 隨風向角改變 CV呈現明顯的先增大后減小的整體趨勢. 在來流風方向當山體處于橋體下風側時，山體對來流風的阻擋引起風沿崖壁折向橋體的回流會使結構的CV增大，但因考慮當風向與崖壁垂直時懸崖對風能量的消耗也最大，因此， CV最大值未出現在90°.

CH呈現出先增大后減小、再增加后減小的趨勢，其最大值出現在25° 附近. 隨著風向角繼續增大，風向與結構阻力方向（橫橋向）夾角逐漸減小，至 90° 達到最小， CH達 到最小值. 而后 CH向相反方向增大至155° 附近達到最大，因山體在來流向的遮擋導致結構處平均風速降低， CH減小.

CM大體呈現先減小后增大再減小的趨勢，0°和 + 3°風攻角 CM最大值出現在 10° 附近， - 3°風攻角 CM最大值出現在 135°. + 3° 和 0° 攻角在 90° 附近 CM減小到 0，而 - 3° 攻角在 45° 附近 CM已減小至0，且方向改變， + 3° 攻角下的扭矩系數方向基本沒有變化.

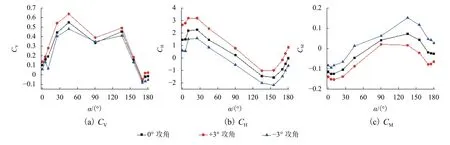
圖3 三分力系數曲線Fig.3 Curves of aerostatic force coefficients

3 抖振響應結果及分析

3.1 抖振響應試驗結果

根據《公路橋梁抗風設計規范》[9]（以下簡稱《橋規》）對限幅振動計算的規定，將此類廊橋結構視為橋梁的單懸臂狀態，依據相關力學知識可知此類結構最大位移響應將發生在懸挑最外緣，試驗選取該點進行測量.

經對各工況試驗數據處理分析，得到模型在紊流場中的風致響應. 在3種風場、2種風速、3個攻角下，實橋橫向、豎向及扭轉3個方向的位移響應均方根（σx、σy、σθ）隨風向角變化的曲線如圖 4所示.

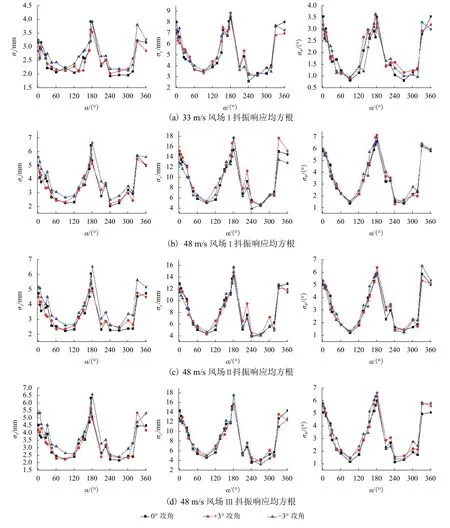
圖4 各風場抖振響應變化曲線Fig.4 Structural buffeting responses in different wind fields

3.2 抖振響應結果分析

3.2.1 抖振響應隨風向角的變化趨勢

由圖4可以看出，當結構位于山體上風側（0°～180°）時，σx、σy、σθ均呈現明顯的先減小后增大趨勢，當山體處于結構側面（0°附近）或部分山體位于結構上風側（180° 附近）時，山體會引起來流風紊流度增大，致使結構響應均方根較大，因此結構處于 45°～135° 風向角內時其響應均方根較小，90°附近達到最小，其余風向角下結構響應均方根較大，且在180° 附近達到最大.

對于橋梁結構，其不僅受法向來流風影響很大，在具有一定風向角的斜風作用下結構具有同樣大的不利影響[10-11]. 再考慮到結構所處當地風環境，國內外諸多學者已做了相當的實驗，發現結構最不利響應值通常出現在與結構法向具有一定角度的斜風作用下，在懸挑屋蓋中也觀察到類似的現象[12]. 因此需對此類地處復雜山區的懸挑結構在斜風作用下的風致響應引起足夠的重視.

當結構位于山體下風側（180°～360°），在來流向隨著山體對結構遮擋面積的增大，結構尖端各響應均整體呈現減小的走勢，但在來流向山體剛好遮擋在結構尖端附近時，引起結構尖端局部紊流度增大，致其抖振響應增大，即風向角在180°～360° 范圍內抖振響應整體呈現先減小后增大的趨勢，且在225° 及 300° 附近出現局部峰值. 觀察結構在山體上風側（60°～120°）和結構處在完全被山體遮擋的下風側（240°～300°），引起前者結構響應的脈動風主要由來流風的脈動成分提供，后者在此基礎上加之由山體及橋塔引起的脈動成分. 雖然后者結構被山體及橋塔遮擋，但其抖振響應并未呈現整體低于前者的態勢，甚至部分響應高于前者. 因此抖振響應不僅要考慮橋塔風效應的影響[13]，山區風環境下結構位于山體下風側時地形的干擾亦需加以重視.

3.2.2 風攻角對抖振響應的影響

在同一風速下，不同風攻角下的抖振響應變化趨勢大體相同，同一風向角下各攻角抖振響應差值相對較小，僅在個別位置出現較大差異，且沒有明顯的規律，可以發現在此 ± 3° 較小幅度范圍內，不同風攻角對結構抖振響應的結果影響不大.

3.2.3 風速對抖振響應的影響

通過2種不同風速下所得抖振響應值發現，風速對結構抖振響應隨風向角改變的變化趨勢幾乎沒有影響，但其對各響應值的影響較為顯著，較高風速下各抖振響應值均明顯大于低風速下的各項響應值. 比較發現，本次試驗較高風速約為低風速的1.5倍，高風速下 σx約為低風速下 σx的1.5倍， σy約為低風速的1.8倍， σθ約為低風速的1.9倍. 風場II和風場III同樣進行了2種風速的試驗，結果與風場I相同，抖振響應圖不再贅余.

3.2.4 紊流度對抖振響應的影響

在設計風速下，通過比較風場I和風場II結構抖振響應值探討紊流度I的改變對結構抖振響應的影響，發現I的變化對不同方向抖振響應的影響不同. 當結構位于山體上風側時，I的變化對 σx影響較小. 但隨著I的增大 σy及σθ有較大變化，雖然其隨著風向角的變化沒有明顯的規律性，但在各風向角下均明顯增大. 由表1可知風場I較風場II的Iu增大約 40.7%，Iw增大約 46.4%. 在此定義 ?σIi為隨I的增大各抖振響應的增幅，由式（1）計算.

式中：i為 x、y、θ；σIi、σIIi分別為 I類和 II類風場橫向、豎向、扭轉抖振響應均方根； ?σIi分別為由紊流度變化引起的橫向、豎向、扭轉抖振響應均方根的增幅.

在設計風速下3種抖振響應增幅隨I增大的變化情況如圖5所示，并將各工況下 ? σIi變化情況匯見表2.

3.2.5 紊流積分尺度對抖振響應的影響

紊流積分尺度是脈動風中紊流渦旋平均尺寸的量度，其大小決定了脈動風對結構作用的影響范圍，如果紊流渦旋增大至可以將結構包含其中，則結構各部位所受的脈動風荷載會疊加，相反，脈動風荷載可能會互相抵消[14]. 通過比較在設計風速下的風場II和風場III中廊橋結構抖振響應值探討積分尺度L的改變對結構抖振響應的影響. 由表1可知，風場III較風場II ，Lu增大約20.1%，Lw增大約23%. 在此，定義?σLi為隨L的增大各抖振響應的增幅，由式（2）計算.

式中： ? σLi為對應由積分尺度變化引起的各響應增幅； σIIIi為III類風場抖振響應均方根.

在設計風速下各抖振響應隨L增大的變化情況如圖6所示，并將結果匯總于表3.

由圖6發現L變化對不同抖振響應影響不同.L的改變對 σx幾乎無影響，各風向角 σy隨L的增大整體呈現增大的趨勢，各風向角 σθ在 ± 3° 攻角下隨L的增大整體增大，但在0° 攻角下受L影響較小.

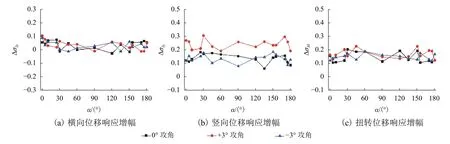
圖5 各抖振響應隨紊流度改變的增幅Fig.5 Increments of buffeting responses with the variation of turbulence intensity

表2 紊流度的變化對結構抖振響應的影響Tab.2 Effects of variation of turbulence intensity on the structural buffeting responses

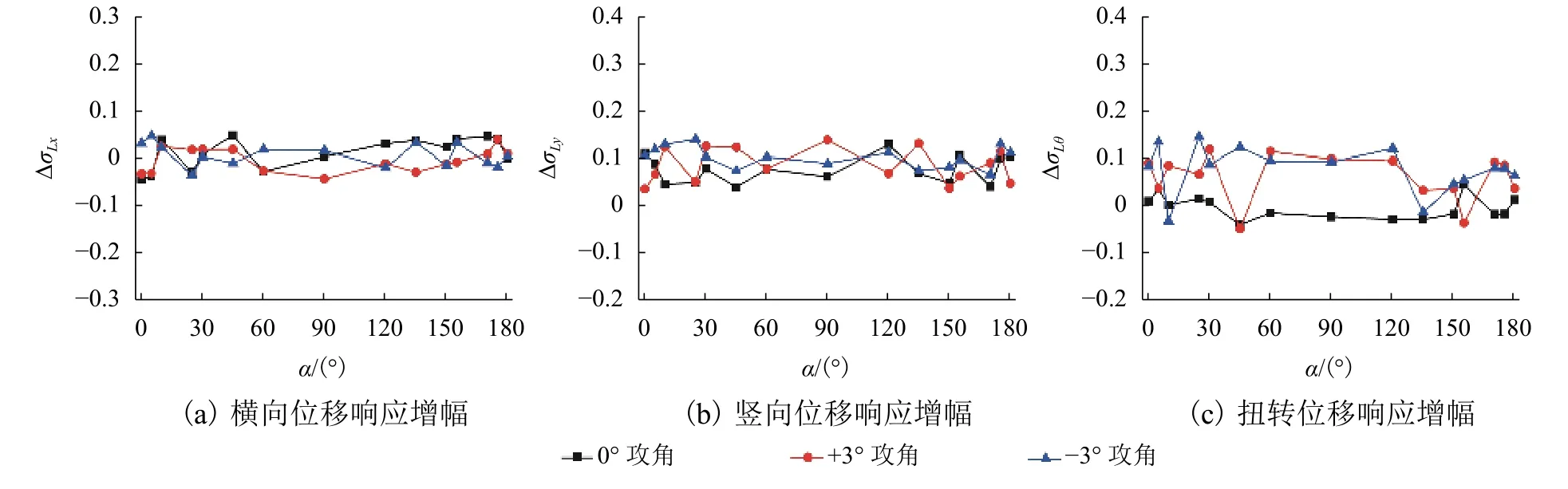
圖6 各抖振響應隨紊流積分尺度改變的增幅Fig.6 Increments of buffeting responses with the variation of turbulence integral scale

表3 紊流積分尺度的變化對結構抖振響應的影響Tab.3 Effects of variation of turbulence integral scale on the structural buffeting responses

4 等效風荷載

自然風產生的風荷載由兩部分組成：平均風作用產生的平均風荷載；脈動風引起的動力風荷載. 通常將后者分為脈動風的背景作用和結構慣性力作用. 現行各國橋梁抗風規范中計算一般只考慮順風向風荷載，且對于順風向風荷載的計算通常都忽略脈動風中與結構自振頻率相近而產生的共振響應.《橋規》在橋梁靜力風荷載作用計算時，可僅考慮靜陣風荷載，且因抖振慣性力與平均風效應和背景脈動效應不能直接疊加，該規范靜陣風荷載的計算方法亦為忽略抖振慣性力，在設計中將導致結果偏小，使設計偏于不安全. 該部分計算復雜且較難把握，為此將脈動風荷載等效為響應相同的靜力風荷載成為十分有效的手段[3]. 鑒于此類人行橋梁結構與傳統橋梁在外形及力的分配等方面存在明顯的差異，其等效風荷載的獲得有待研究，以便用于設計.根據實際地形情況，將橋址地形視為B類風場（抖振試驗中風場I即為B類風場）進行計算分析.

對于橋梁結構來說，《橋規》中將平均風作用和風的背景脈動兩部分合并，定義靜陣風系數 GV為總響應與平均風響應之比，并給出了不同地表類別隨水平加載長度變化的 GV的取值表格.

依據《橋規》可得結構在橫橋向風荷載作用下主梁單位長度上的橫向等效風荷載為[9]

式中： FH為作用在主梁單位長度上的靜陣風荷載；ρ為空氣密度； U0為靜陣風風速；H為主梁投影高度.

根據隨機振動理論，響應譜 Sx(ω) 、速度譜Sv(ω) 、 加速度譜 Sa(ω) 的關系為

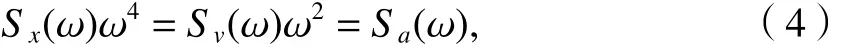
式中： ω 為圓頻率.

本文抖振試驗為結構在脈動風作用下產生的總的抖振響應. 因此可根據風洞試驗抖振響應值，按照抖振慣性力計算公式[15]得到結構所受脈動風荷載，并與基于三分力系數結果得到的平均風荷載整合，獲得結構靜力等效風荷載.

結構每延米脈動風荷載為

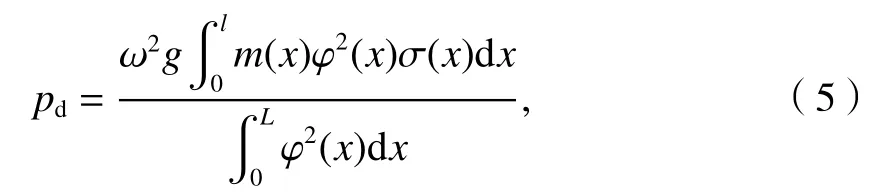
式中： g 為峰值因子； l 為主梁長度； m (x) 為單位長度主梁質量； φ (x) 為 結構振型； σ (x) 為抖振位移響應均方根； x 為橋軸向坐標.

平均風荷載：

式中： U 為平均風速.

結構靜力等效風荷載為

結構阻力系數及等效風荷載最大值出現在25°風向角，根據式（3）～（7）計算得到橋梁規范及基于風洞試驗結構最大橫橋向等效風荷載計算結果如表4，表中計算誤差值為以風洞試驗值為基礎的《橋規》計算結果的誤差值，即為二者差值與試驗值的比值.

表4 等效風荷載計算結果Tab.4 Results of equivalent wind loading

文中觀景廊橋屬人行橋梁，但結構與傳統橋梁結構有明顯區別. 此結構固有頻率高（結構一階橫向頻率高達2.41 Hz）、剛度大，為特殊的單懸臂結構，且主梁包含箱梁及桁架梁兩種結構形式. 通過橋梁規范以及風洞試驗響應值對結構等效風荷載的計算比較發現，利用橋梁規范的計算結果明顯高于試驗值，規范設計偏于安全. 橋梁規范的計算忽略了脈動風譜中與結構自振頻率相近的共振部分，通過靜陣風系數將平均風作用和風的背景脈動放大得到二者的綜合效應，即為靜陣風荷載. 在將風的作用僅當作靜力作用考慮并忽略共振部分原本是偏于不安全的，但因該結構水平加載長度小，頻率高，共振部分影響小，按規范取值中靜陣風系數過大，使靜力風荷載作用放大較多，風荷載計算結果高于試驗值30%，即使用橋梁規范計算該結構等效風荷載過于保守，對于此類結構橋梁規范的計算方法及靜陣風系數取值有待商榷及進一步分析. 通過風洞試驗獲得的結構靜力等效風荷載，綜合考慮了平均風、脈動風的背景脈動，以及脈動風引起的共振部分，其每延米結構等效風荷載可直接用于結構設計.

5 結 論

（1） 隨著風向角改變，結構三分力系數呈現規律的變化趨勢，山體對三分力系數影響顯著，其對來流風的阻擋導致平均風速的降低使阻力系數減小，且來流風沿崖壁向上的回流會使升力系數增大.

（2） 風向角在 0°～180° 和 180°～360° 內變化，抖振響應呈現明顯先減小后增大的走勢，結構在一定偏角的斜風作用下抖振響應達到最大，且當結構位于山體及橋塔下風側時其抖振響應可能高于上風側，結構設計時需加以重視.

（3） ± 3° 小幅度范圍內風攻角對抖振響應的結果影響不大. 因同一風場風速不同引起標準差的變化，較高風速下各響應值明顯大于低風速各響應值.

（4） 結構橫向抖振響應受紊流度的變化影響較小，豎向及扭轉響應隨紊流度的增加增幅較大.

（5） 紊流積分尺度的變化對結構橫向抖振響應幾乎無影響，隨著紊流積分尺度的增大，豎向響應相應增大，扭轉響應在 ± 3° 攻角下整體增大，但在 0°攻角下受積分尺度影響較小.

（6） 針對此類頻率高、剛度大的單懸臂結構，《公路橋梁抗風設計規范》對結構等效風荷載的計算偏于保守，靜陣風系數取值有待修正. 基于試驗獲得的等效風荷載綜合考慮了平均風及脈動風作用，可直接用于結構設計.