一種新型單層網殼節點的力學性能研究

蔡 健 ，王永琦 ，陳慶軍 ，姜正榮 ，錢 泉 ，左志亮

（1. 華南理工大學土木與交通學院，廣東 廣州 510641；2. 華南理工大學亞熱帶建筑科學國家重點試驗室，廣東 廣州 510641）

對于以剛度作為設計控制條件的大跨度空間結構而言，節點剛度十分重要. 在相同截面周長下，圓形截面桿件的截面剛度往往小于矩形截面，這使其具有存在并發展的技術空間[1]. 在單層網殼結構中，節點起著連接匯交桿件、傳遞荷載的作用. 結構的傳力路徑可能隨著節點的失效不斷發生改變，進而導致結構體系的局部破壞甚至整個體系的連續性倒塌[2-4]. 因此，節點剛度將直接影響結構的整體穩定性、變形及內力分布等[5-6].

對于焊接矩形鋼管空間網殼而言，我國目前最常用的焊接空心球節點和螺栓球節點無法滿足建筑設計要求，同時，此兩類節點被看作是鉸接[7]或半剛接[8]，低估了節點的作用并浪費了材料[9-10]. 而空間鑄鋼節點制作也比較復雜，如何研制一種構造簡單施工方便的節點形式是空間結構中的熱點問題. 文獻[11]提出了計算平面X形矩形鋼管相貫節點平面外抗彎剛度的公式. 此外，王先鐵等[12]、陳敏[13]針對單層網格結構分別設計了一種新型節點.

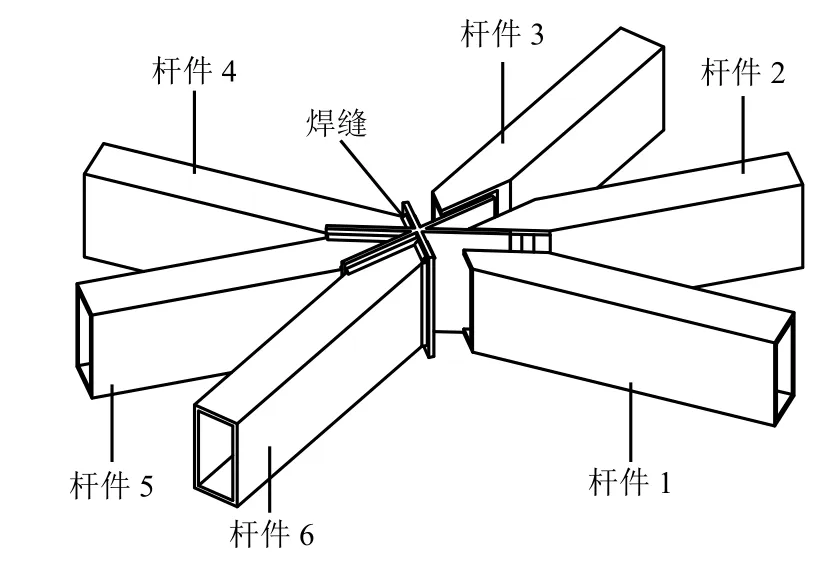
圖1 新型焊接端板節點Fig.1 New type of welded end-plate joint

本文針對國內某空間網殼工程，研究了一種如圖1所示的適用于矩形截面鋼管網殼的新型焊接端板節點，該節點由桿件及端板組成. 桿件端部按照節點端板的角度切割、剖平并焊接. 具有便于施工、剛度大及經濟性等優點. 而目前沒有關于該種新型節點的研究，為掌握該種節點的受力性能，推廣該種節點的應用，本文以實際工程為背景，通過試驗及數值仿真分析對該節點的受力性能進行研究.

1 試驗方案

1.1 節點選取

為研究該新型節點的受力性能、承載能力及破壞機理，試驗選取采用該新型節點的某工程中較危險區域處的截面尺寸為 400 mm × 200 mm ×12mm ×12 mm的箱型截面節點進行相關研究.

考慮到試驗加載設備、反力架的性能以及幾點的尺寸因素，采用1∶2的縮尺模型進行試驗，取桿件截面為 200 mm × 100 mm ×6mm ×6mm. 在圖 2試件平面圖中，將八邊形包圍的區域稱為節點區，其它區域稱為桿件. 為避免加載時由于桿件太長而引起的桿件先破壞的情況，桿件不宜太長；而根據圣維南原理，為減小邊界條件對節點區受力性能的影響，桿件長度不應太小. 因此，首先根據經驗將桿件長度取為2.5h （h為桿件截面高度）. 為方便加載及固定，在每根桿件端部焊接一塊尺寸為280 mm × 180 mm ×20 mm的端板. 試件具體尺寸詳見圖2. 通過材性試驗得到的鋼板力學性能指標見表1.

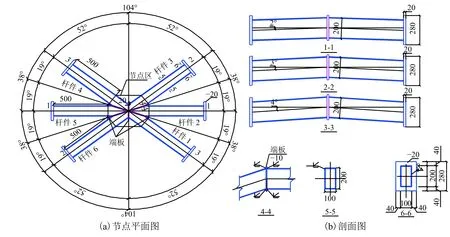
圖2 試件詳圖Fig.2 Details of the joint

為驗證桿件長度取值2.5h的合理性，選取截面為 400 mm × 200 mm ×12mm ×12mm，長度為2m的桿件進行多尺度模型分析. 在有限元分析軟件ABAQUS中分別建立全梁單元模型、全殼模型以及梁殼單元多尺度模型，其中多尺度模型由長度分別為2.5h （1 m）的梁單元區域和殼單元區域組成. 鋼材采用理想彈塑性本構模型，彈性模量及屈服強度分別取為206 GPa和345 MPa. 桿件底部固接，在頂端施加平行于短邊的水平力. 從圖3可以看出，桿件長度取為2.5h是合理的.

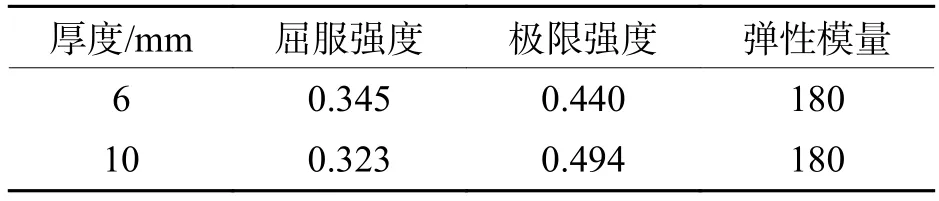
表1 材性試驗結果Tab.1 Material properties of the test specimens GPa

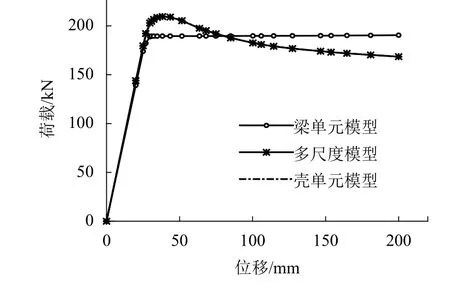
圖3 多尺度分析結果Fig.3 Results of multi-scale analysis

1.2 加載方案及裝置

運用結構計算軟件3D3S. v9.0對整體結構進行分析計算，按照規定添加荷載工況組合. 計算結果表明軸力、彎矩、剪力和扭矩對每根桿件同時產生影響，但軸力的作用最明顯，其它作用可以忽略. 因此本試驗只進行節點受壓極限承載力試驗. 試驗在可以承受20 000 kN荷載的自平衡反力架中進行，加載裝置如圖4所示.

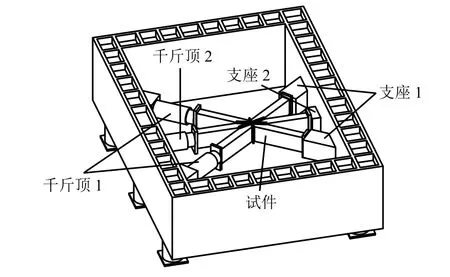
圖4 試驗加載裝置Fig.4 Test setup

桿件4～6端固定在反力架上，經前期研究表明，當3根桿件中施加相同軸力時，接近最不利荷載的布置. 因而通過千斤頂分別對桿件1～3施加大小相等的軸力. 加載過程分為預加載及正式加載. 前者分3級，每級施加荷載50 kN. 根據有限元分析結果，試件在桿件1～3中軸力達到800 kN左右時開始出現屈服. 因此在進行試驗時，在0～300 kN荷載階段，每次施加100 kN；在荷載小于700 kN時按照每級50 kN進行加載；此后每級加載降為30 kN直至試件屈服；緊接著根據位移來調整加載值，直至破壞.

本次試驗共布置了60個應變片、16個應變花、10個精度為0.01 mm的位移計和2個力傳感器，分別用于測量應變、位移及軸力. 通過東華DH3816靜態數據采集儀自動采集數據，各測點位置見圖5. 圖中應變片編號用應變片0° 和90° 方向片編號來表示，如“17-19”代表測點17～19組成的應變花.

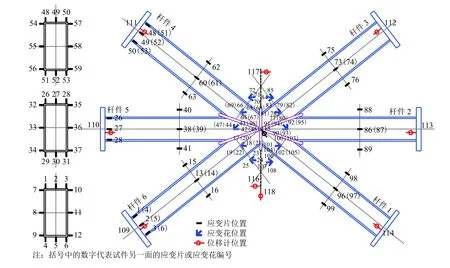
圖5 測點布置Fig.5 Layout of the strain gauges

2 試驗結果及分析

2.1 試件破壞過程

（1） 當荷載小于550 kN時，試件變形較小，僅測點51、56、100應變達到屈服. 由于這些測點處于節點區或支座角部，存在應力集中現象，所以應變較大.

（2） 當荷載大于 600 kN時，測點 42、70均屈服，且新的屈服點隨著荷載的增大而出現.

（3） 當荷載大于823 kN時，雖然節點區凹面和側面測點已經屈服，但是桿件仍然處于彈性狀態.

（4） 當荷載大于1 176 kN時，軸壓無法繼續維持，節點變形突然增大，試件宣告破壞. 此時，桿件1～3與節點區交接處及桿件4～6與支座連接的端部出現明顯的局部屈曲. 試件破壞時的形態見圖6.

2.2 荷載-應變曲線

通過等效應變強度求得應變花的應變強度. 圖7給出了節點區各測點荷載-應變強度. 其中，荷載代表縮尺模型相應桿端軸力. 從圖中可以看出試件的凹面測點100～102 （桿件1根部）最先進入塑性，隨后節點區側面測點70～72 （桿件 4）、測點106～108（桿件1）也進入塑性，并發展較快. 節點破壞時，節點區大部分測點應變突然增大，出現明顯轉折，說明節點區鋼板已經屈曲.

圖6 節點破壞形態Fig.6 Failure modes of the joint

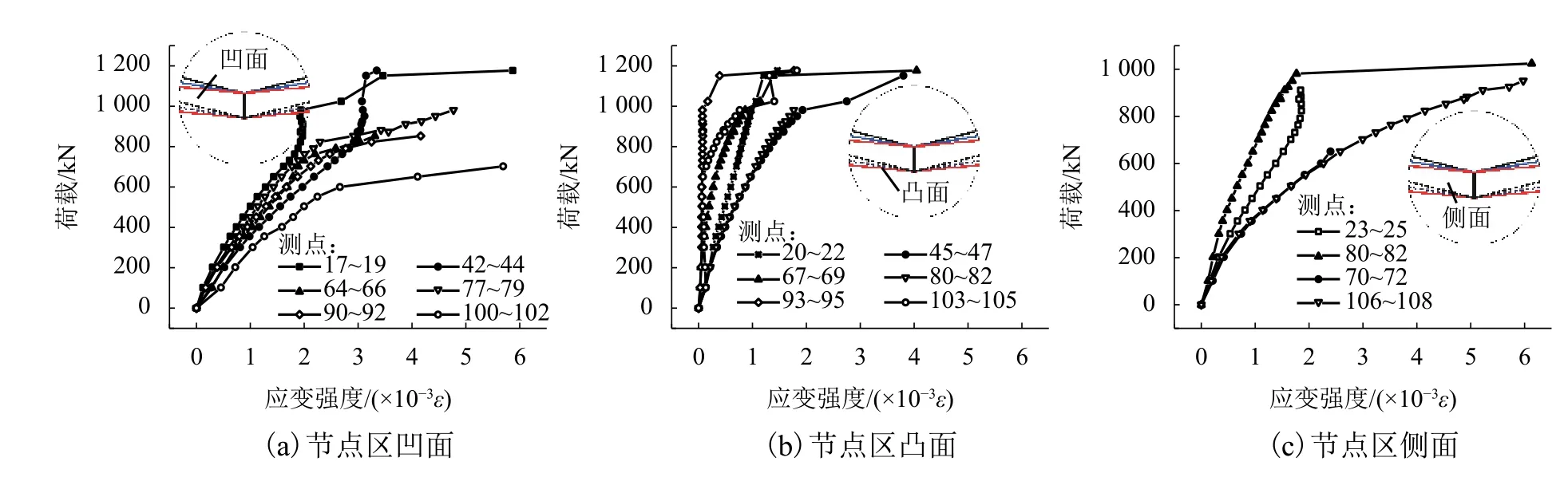
圖7 節點區測點荷載-應變強度曲線Fig.7 Load-strain intensity curve of different parts of the joint

圖8 給出了桿件1、2和3中截面測點的荷載-應變曲線. 從圖中可以看出，在試件破壞前，除桿件5外，其他測點的荷載-應變曲線均近似為直線，說明在試件整體破壞前均處于彈性狀態.

2.3 荷載-位移曲線

圖9給出了各加載端荷載-位移曲線，可以看出該節點從加載開始到結束經歷了3個階段：（1） 彈性階段：曲線為直線，且3條曲線的較剛度一致. 而桿件2的位移偏大，分析原因為焊接造成了試件端板發生彎曲和各部件間的空位. （2） 彈塑性階段：當荷載大于600 kN時，測點開始屈服，但塑性區發展緩慢，試件整體承受荷載的能力不受影響. （3） 塑性破壞階段：當荷載大于981 kN時，節點塑性區開展較為嚴重，變形明顯增大，直至破壞. 從圖10節點中點荷載-豎向位移曲線可以看出，隨著節點從彈性階段進入屈服階段，其豎向位移從0開始逐漸增大，直到破壞.

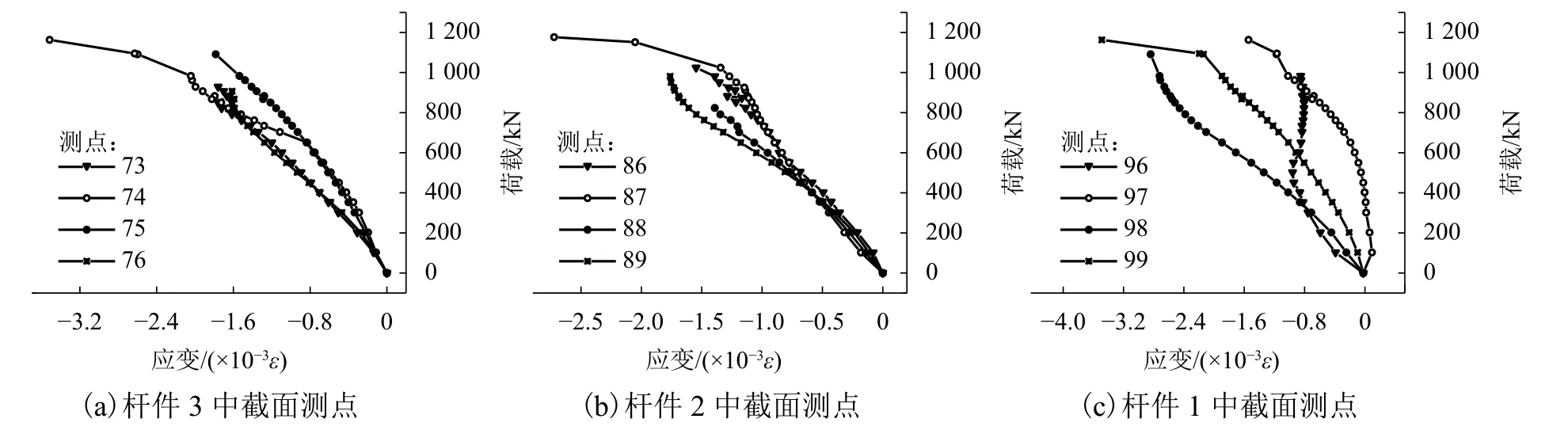
圖8 節點區測點荷載-應變曲線Fig.8 Lload-strain curve of different parts of the joint

圖9 桿端荷載-位移曲線Fig.9 Load-axial displacement curve of different bars

3 有限元分析

3.1 有限元模型

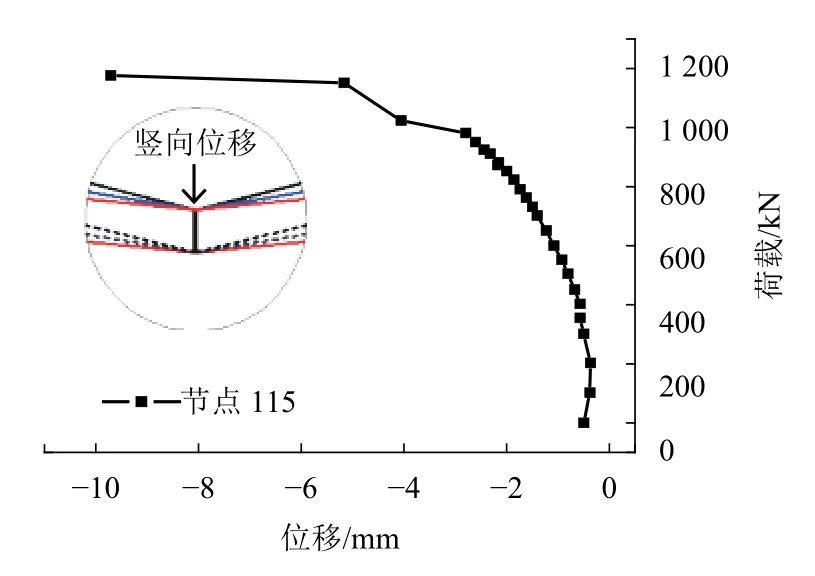
圖10 節點區中心點荷載-豎向位移曲線Fig.10 Load-vertical displacement curve in the center of the joint

本文采用有限元分析軟件ABAQUS對此試驗結果進行仿真分析. 通過約束設置在桿端截面參考點的自由度來模擬實際加載端或固定端. 模型采用雙線性彈塑性模型，泊松比取0.3，其它材料參數見表1. 采用Von-Misess屈服準則及相關的流動法則控制材料彈塑性的發展和單元剛度. 由于模型中桿件壁的寬厚比小于15，故采用一階4節點四邊形有限薄膜應變線性減縮積分殼單元S4R來模擬節點單元. 其中，節點區和桿件的單元尺寸分別為10 mm和20 mm，總單元數為9 753.

通過一系列有限元模型計算發現空間網殼焊接端板節點在破壞前變形均較小且有極值點，且進入塑性后荷載-位移曲線有水平段，因此，這里取極值點作為極限承載力.

3.2 試驗結果與有限元結果比較

圖11比較了試驗及有限元模型加載端的荷載-位移曲線. 可以看出試驗所得屈服荷載及極限荷載偏大，平均差值分別為1.40%和5.07%，而有限元分析結果的剛度較大. 原因除有限元分析結果的普遍特征之外，主要有：（1） 焊縫的存在有助于試件承載力的提高和剛度的降低[14]；（2） 焊接變形引起桿件端部蓋板向外弧彎明顯，使測得的位移偏大；（3） 有限元分析所取本構與試驗材質的差異.

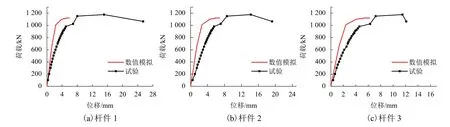
圖11 桿件荷載-位移曲線Fig.11 Load-displacement curves of the joint

圖12 列出了部分測點的荷載-應變曲線. 可以看出兩者在彈性階段吻合良好，而在由彈性階段向塑性階段發展的過渡階段有一定的偏離. 分析原因為測點選取誤差及邊界條件差異.

圖12 部分測點荷載-應變曲線Fig.12 Load-strain curve of some spots on the joint

整個節點破壞時的應力分布見圖13，其中，桿件在固定支座的下部以及節點區的連接處應力較大，但僅僅分布在一個較小的范圍內. 節點端板的應力在靠近加載端出現較大、較集中的分布.

圖13 節點破壞時應力分布Fig.13 Distribution of stress in the joint

4 參數分析

在前章研究的基礎上，通過創建有限元模型探討桿件間水平夾角α、桿件平面外角度β、端板壁厚t2與桿件壁厚t1比值等幾何參數對該類型節點受力過程、破壞模式以及極限承載力的影響規律.

為表述方便，將節點以形式 β1-β2-β3-α-t1-t2進行命名，其中 β1、β2及 β3分別代表桿件 2、5 和桿件 3、6以及桿件1、4與水平面間的夾角. 若t2項為0，則表示未設置節點端板. 各角度含義見圖14.

參考《鋼結構設計規范（GB50017—2003）》[15]中的規定，為使焊根能夠熔透，兩桿件軸線間夾角不得小于30°，同時參照一般建筑造型的尺寸，本文在選取節點分析參數時將α限定在30°～75° 之間，而將β限定在0°～8° 之間，桿件腹板及翼緣分別取為200 mm和100 mm，各分析參數見表2.

在此次限元分析中，不考慮鋼材的強化階段，而將其作為節點設計的安全儲備. 取鋼材的屈服強度fy= 345 MPa，彈性模量 E = 206 GPa，泊松比 ν = 0.3.

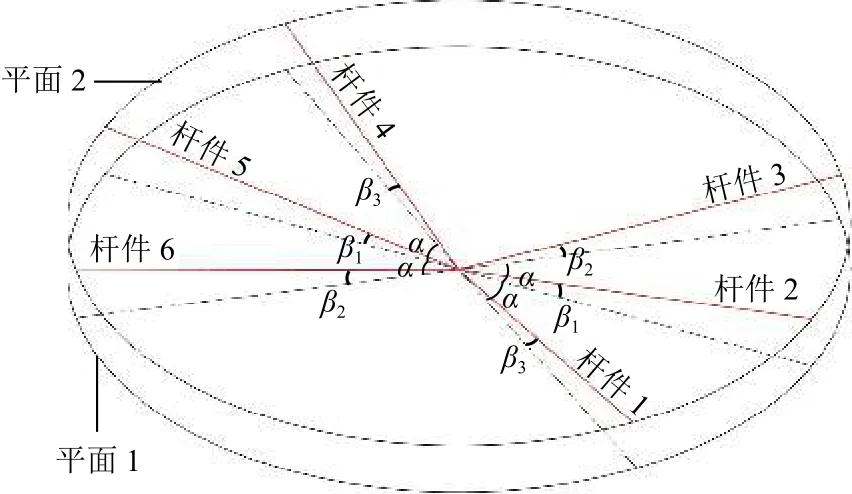
圖14 各角度含義Fig.14 Meaning of different angles

表2 分析參數Tab.2 Parameters for analysis

4.1 節點端板設置合理性驗證

為驗證節點端板設置的意義，分析了4種不同參數的節點. 圖15給出了節點端部荷載-位移曲線.

以上比較說明合理的設置節點端板可以提高節點的承載力和剛度，進而改善節點的受力性能.

4.2 節點破壞形態分析

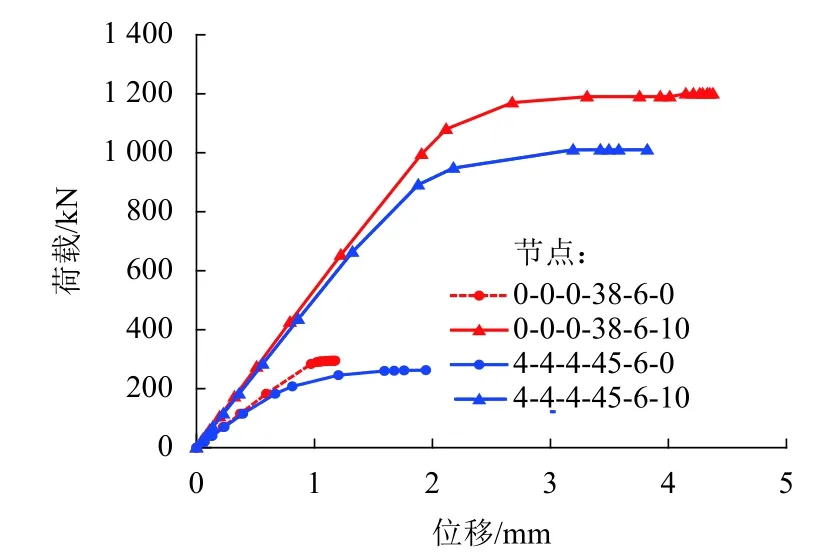
圖15 不同節點荷載-位移曲線Fig.15 Load-displacement curves for different joints

本文在描述節點破壞模式時，不討論支座端部的破壞情況. 通過對大量有限元模型進行統計分析，根據節點區與桿件承載力的強弱關系將節點的破壞模式分為5種，表3列出各種破壞模式.

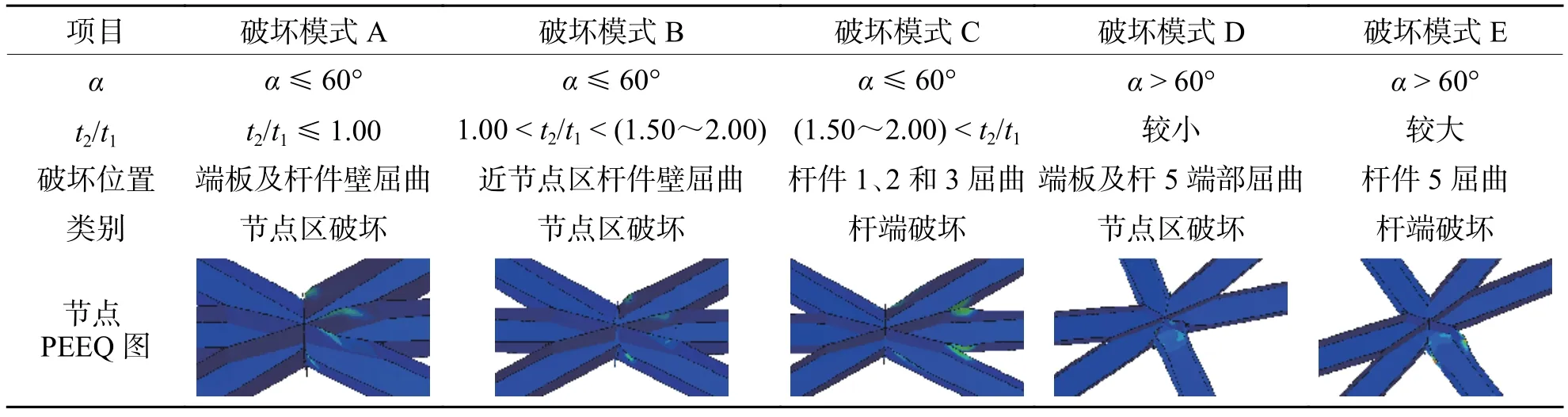
表3 節點破壞模式及條件Tab.3 Failure modes of joint and conditions

4.3 極限承載力

根據有限元計算結果，圖16繪制了參數α、β、及t2/t1對極限承載力的影響. 從圖中可以看出：

（1） 隨著節點端板厚度的增大，節點剛度、屈服承載力以及極限承載力呈增大的趨勢. 隨著β1-β2-β3的增加，節點區產生的彎矩也增加，而抗壓剛度逐漸下降. 當 30° ≤ α ≤ 60° 時，節點剛度與 α 成正比，在 α ＞ 60° 時成反比.

（2） 若平面外角度一定，則當 α ≤ 60° 時，節點的極限承載力在t2/t1＞ 2.00時趨于穩定；反之，節點的極限承載力在t2/t1＞ 1.67時趨于穩定.

（3） 當 α ＞ 60°時，若節點破壞形態為節點區破壞（即破壞模式D），則節點極限承載力隨著α的增大而增大；若節點破壞形態為桿端破壞（即破壞模式E），則節點極限承載力隨著α的增大而減小.

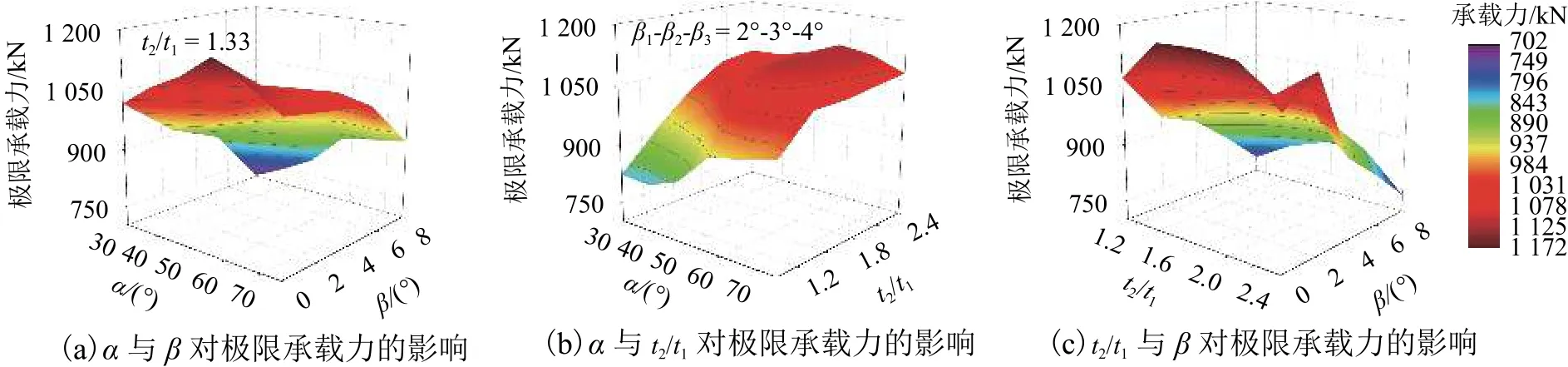
圖16 極限承載力影響Fig.16 Factors for ultimate strength

5 節點承載力計算方法

為將該節點推廣到實際工程中，現提出該節點在桿件全部受壓情況下的極限承載力的簡化計算方法. 根據前面的討論，考慮各幾何參數對節點極限承載力的影響，提出了極限承載力計算公式：

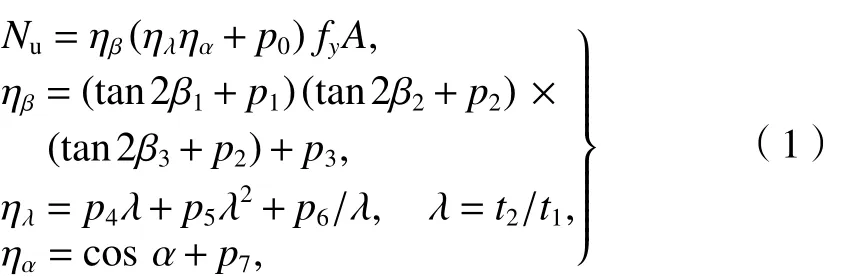
式中：Nu為節點的極限承載力；ηβ為參數β對節點承載力影響系數；ηλ為參數t2/t1對節點承載力影響系數；ηα為α對節點承載力影響系數；A為桿件橫截面面積；p0～p7為待定系數.

參考《網殼結構技術規程（JGJ7—2010）》[16]對焊接空心球節點安全系數的取值，本文取空間網殼焊接端板節點承載力安全系數K = 1.60，則空間網殼焊接端板節點的設計承載力N = Nu/K = 0.625Nu，根據上述分析結果，發現節點極限承載力在水平夾角為60° 前后會出現不同情況，因此，本章在對空間網殼焊接端板節點極限承載力回歸分析時將分為α ≤60° 和 α ＞ 60° 兩種情況進行討論.

5.1 水平夾角 α ≤ 60°的情況

根據表2中節點分析參數的范圍，運用有限元軟件ABAQUS分析了164個α在30°～60°之間的空間網殼焊接端板節點模型. 通過對計算結果進行多元非線性回歸擬合，得出節點在本文所討論的加載條件下式（1）中各參數所對應的值為

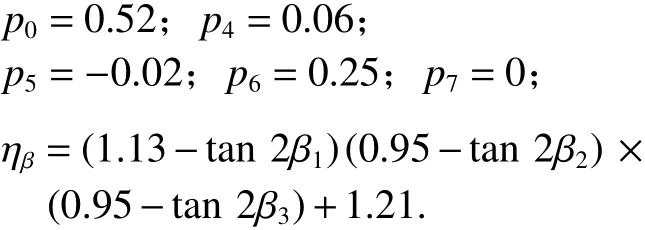
當 λ ＞ 2時，取 λ = 2. 該情況下計算得到節點極限承載力與有限元結果的最大誤差為7.32%，Nu/NFEA的平均值為0.985（其中，NFEA為由軟件計算分析得到的極限承載力），相關系數為0.9915，方差為0.000 79. 圖17給出了式（1）的計算結果與有限元結果的對比情況.

5.2 水平夾角 α ＞ 60° 的情況

運用有限元軟件ABAQUS分析了70個α位于60°～75°之間的空間網殼焊接端板節點模型，分析參數范圍參見表2，通過對計算結果進行多元非線性回歸擬合，得出節點在本文所討論的加載條件下的極限承載力為

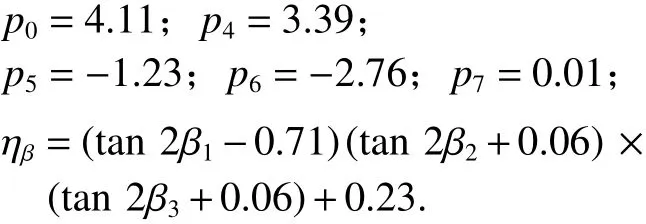
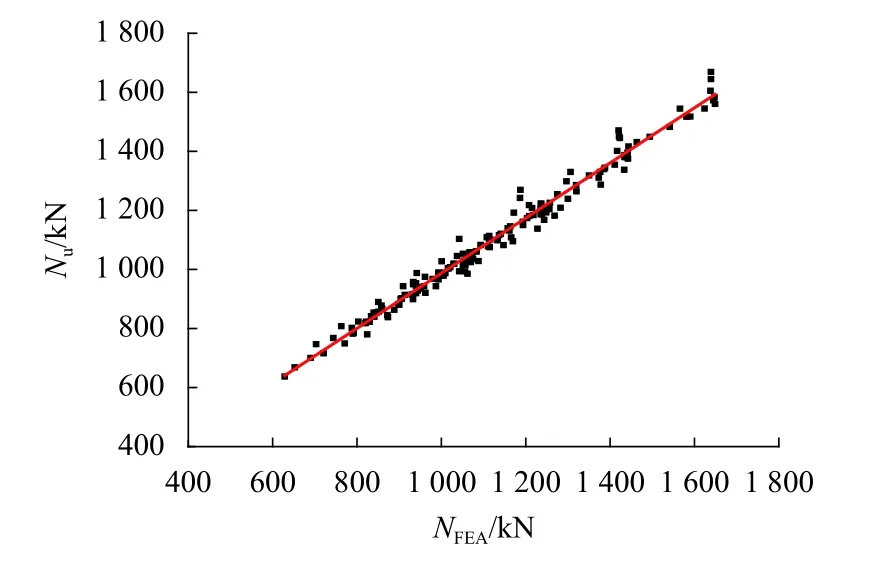
圖17 α ≤ 60°時的擬合結果Fig.17 Fitting result for α ≤ 60°

當λ ＞ 2時，取λ = 2. 該情況下計算得到節點極限承載力與有限元結果的最大誤差為7.81%，Nu/NFEA的平均值為0.989，相關系數為0.9875，方差為0.000 99.圖18給出了式（1）的計算結果與有限元結果的對比情況.

圖18 α ＞ 60°時的擬合結果Fig.18 Fitting result for α ＞ 60°

6 結 論

本文以某工程為背景，通過對其中應用的新型焊接端板節點進行了試驗研究及有限元分析，得出了以下結論：

（1） 對1∶2的縮尺模型進行了受壓承載力試驗研究，結果表明該類型節點具有良好的受力性能.

（2） 通過有限元分析軟件ABAQUS對試件進行數值模擬分析，并將得到的荷載-應變強度曲線、荷載-位移曲線、破壞形態與試驗結果進行對比，結果表明兩者吻合較好，有限元模型能夠用于大規模參數化分析.

（3） 在一定區間內，節點的極限承載力隨著節點端板厚與桿件壁厚比值t2/t1的增大而增大，而與平面外角度β成反比. 水平夾角α對節點極限承載力影響較大，但其在60° 前后影響不同.

（4） 根據有限元分析結果分別對 α ≤ 60° 和 α ＞60° 兩種情況下節點的極限承載力進行了擬合回歸，提出了該節點受壓極限承載力計算公式，結果表明，該公式能較好地計算節點的極限承載力，進而可以作為工程設計的參考依據.

致謝：感謝華南理工大學亞熱帶建筑科學國家重點實驗室自主研究課題項目（2015ZC18）資金的資助.