基于指數平滑法的高考人數預測研究

湯仕琦

摘要：本文第一部分討論了建立指數平滑的預測模型，選擇平滑系數原理，計算初始平滑值。在此基礎上，第二部分借助1977年至2018年高考實際人數值，運用三次指數平滑法對2019年高考人數進行了預測。第三部分總結了在使用指數平滑法時需要注意的幾大方面。

關鍵詞：預測;指數平滑法;平滑系數

一、高考人數變化的因素

高考是我國教育體系中的一個重要的組成部分，高考人數的變化反映了國家的教育培養趨勢，并且成為一個國家在政治方面、經濟方面、文化方面的縮影。影響高考人數變化的因素有很多，在政治、經濟層面隨著國家開放的進一步深入，其他各國與中國在教育資源方面達成共享，國人可以有機會并且有經濟實力選擇出國而放棄國內考試。在文化層面，國人改變了傳統的思維模式，人口出生率下降，適齡兒童也隨之減少，也同樣影響了參于高考的人數。

二、指數平滑預測法

指數平滑法又稱指數加權平均法，由美國學者 R.G.Brown 提出的。這種方法以時間為序揭示其歷史資料的變化規律，常用的指數平滑法包括一次指數平滑、二次指數平滑和三次指數平滑。在實際預測中具體采用哪一種平滑法，要根據時間序列的趨勢性分析確定。

（一）指數平滑法預測模型

一次指數平滑模型為：

為平滑系數，表示在t時間的平滑后數據。

二次指數平滑模型為：

其中St（1）為一次平滑值，St（2）為二次平滑值。二次指數平滑方法是針對指數平滑值再次進行指數平滑的方法，并且通過指數平滑得到的預測數據和實際數值第二次計算。二次指數平滑需要借助一次指數平滑的數值建立新的預測模型。

三次指數平滑法預測模型為：

其中St（1）代表一次平滑值，St（2）代表二次平滑值，St（3）代表三次平滑值。最終建立的預測模型為：=at+bt*l+ct*l2，其中t為當前時期;l為預測時期與當前時期的時間差;為時期的預測值;at，bt，ct為二次曲線修正系數。

（二）初始值和平滑系數的確定

（1）初始值

指數平滑法是一個迭代計算過程，用指數平滑法進行預測計算時，首先必須確定初始值S0（1），S0（2），S0（3）。平滑常數在時間序列較長時，初始值的大小對預測的影響也很小。根據通常計算步驟，當時間序數超過15項的時候，初始值可以直接取第一個實際值。

（2）平滑系數的選擇

平滑系數一般取值在0到1之間的任意數值，其選擇的原則是使預測值與時間觀測序列之間的均方差S和平均絕對誤差最小。

三、指數平滑法在高考人數預測中的實例

數據是預測的基礎。指數平滑法是以歷史數據資料為基礎，能便捷地獲得結果的預測方法。通過預測，可以明晰高考人數的變化規律，提出相關措施，為有效科學地改進選拔制度提供科學決策。

（一）概述

高考恢復40多年來，在這40年里高考人數有增漲有跌落，下面是1977年至2018年參加高考人數變化趨勢統計（見圖1），從表中可以看出，在2008年達到歷史最高峰1050萬人之后急劇下降，直至2014年起開始止跌趨穩，高考人數變化幅度在從長期來看，變動幅度較大。

（二）指數平滑值的計算

（1）初始值

由于數據共有41項，因此可以初始值可以直接取第一個實際值，即其次選取平滑系數α。首先分別選取α= 0.3，0.6，0.9 （見表1）：

（2）平滑系數的確定

根據表 1，可以看出預測結果的準確度與不同的α的取值有很大的關聯。隨著平滑系數α的值增加，平滑結果變得更接近時間序列值，即，誤差變得越來越小。這表明隨著α取值的增大，預測結果的準確性增加。當α= 0.9時，平滑預測的誤差最小，因此認為α應當取取 0.9。

（3）預測值

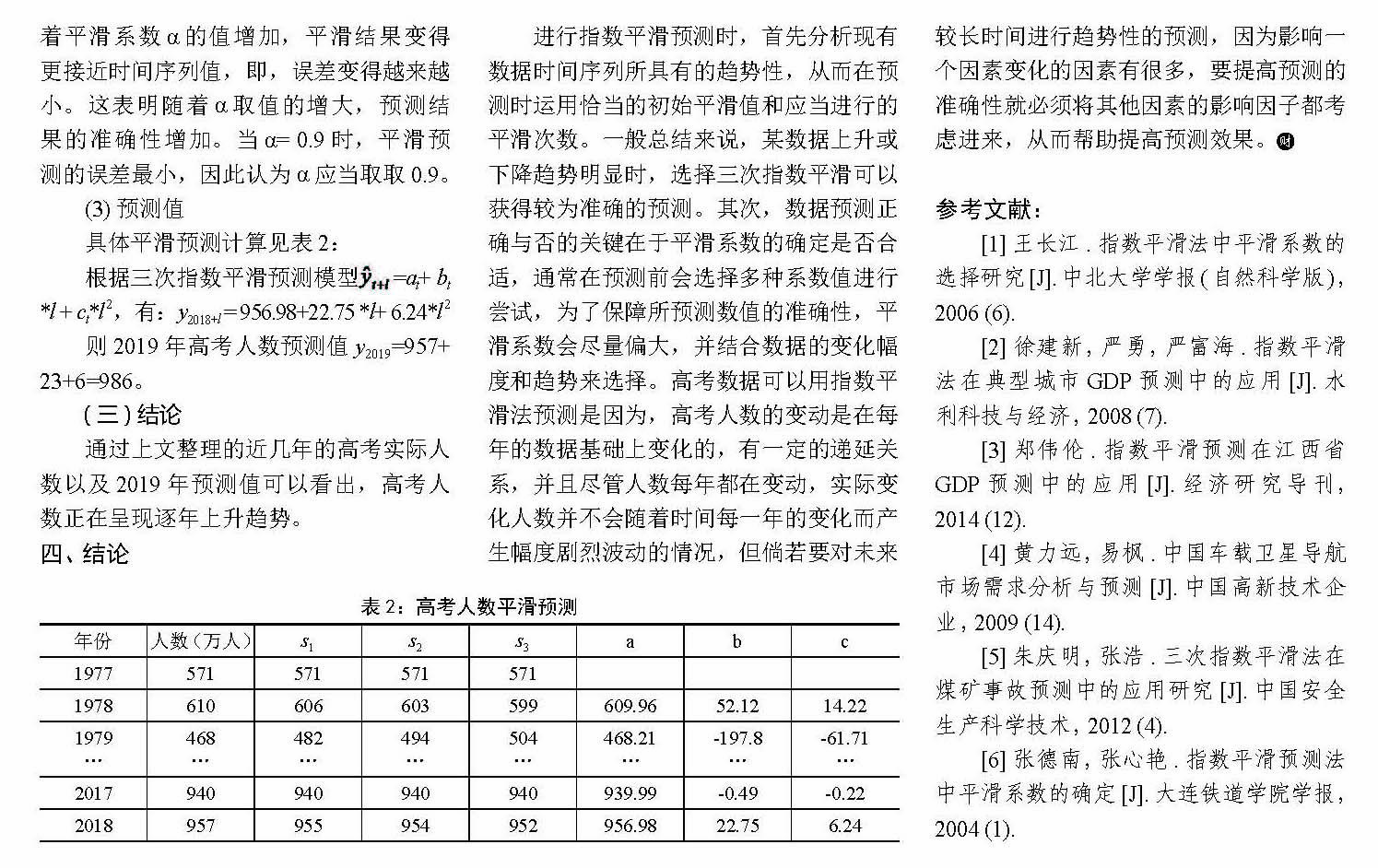
具體平滑預測計算見表 2：

根據三次指數平滑預測模型=at+ bt *l + ct*l2，有：y2018+l = 956.98+22.75 *l+ 6.24*l2

則2019年高考人數預測值y2019=957+ 23+6=986。

（三）結論

通過上文整理的近幾年的高考實際人數以及2019年預測值可以看出，高考人數正在呈現逐年上升趨勢。

四、結論

進行指數平滑預測時，首先分析現有數據時間序列所具有的趨勢性，從而在預測時運用恰當的初始平滑值和應當進行的平滑次數。一般總結來說，某數據上升或下降趨勢明顯時，選擇三次指數平滑可以獲得較為準確的預測。其次，數據預測正確與否的關鍵在于平滑系數的確定是否合適，通常在預測前會選擇多種系數值進行嘗試，為了保障所預測數值的準確性，平滑系數會盡量偏大，并結合數據的變化幅度和趨勢來選擇。高考數據可以用指數平滑法預測是因為，高考人數的變動是在每年的數據基礎上變化的，有一定的遞延關系，并且盡管人數每年都在變動，實際變化人數并不會隨著時間每一年的變化而產生幅度劇烈波動的情況，但倘若要對未來較長時間進行趨勢性的預測，因為影響一個因素變化的因素有很多，要提高預測的準確性就必須將其他因素的影響因子都考慮進來，從而幫助提高預測效果。

參考文獻：

[1]王長江.指數平滑法中平滑系數的選擇研究[J].中北大學學報（自然科學版），2006 （6）.

[2]徐建新，嚴勇，嚴富海.指數平滑法在典型城市GDP預測中的應用[J].水利科技與經濟，2008 （7）.

[3]鄭偉倫.指數平滑預測在江西省GDP預測中的應用[J].經濟研究導刊，2014 （12）.

[4]黃力遠，易楓.中國車載衛星導航市場需求分析與預測[J].中國高新技術企業，2009 （14）.

[5]朱慶明，張浩.三次指數平滑法在煤礦事故預測中的應用研究[J].中國安全生產科學技術，2012 （4）.

[6]張德南，張心艷.指數平滑預測法中平滑系數的確定[J].大連鐵道學院學報，2004 （1）.