讓數學思想之花在初中教學中綻放

施利紅

【摘? ?要】? 數學思想猶如天上的繁星，浩瀚無窮，神秘莫測。作為一名初中數學教師，一定要大膽踐行數學思想方法，逐步讓初中數學思想之花在課堂教學中綻放光芒。

【關鍵詞】? 思想;含義;類型;應用;數學

人教版初中數學新教材體系主要包括明暗兩條主線，所謂明線就是指基本的數學知識，暗線就是指各種數學思想，它是編寫教材的指導思想;明線比較容易理解，暗線不易看懂;明線是圍繞“是什么”編寫，暗線主要強調“為什么”，學生只有在理解暗線的基礎上，才能全方位、深層次理解所學的新知識和新技能。筆者認為，在初中數學課堂教學中，培養學生的數學思想是提高師生互動效率的重要手段。

一、數學思想的含義

數學思想是指人們生活樂園里的空間形式與數學關系反映到腦海里，通過復雜的思維得出言之有理的結論，這既是從本質上理解數學方法和數學內容，又是指導人們探索解決數學問題的原則和觀點;既是對數學規律的理性認識，又是對數學基礎知識和數學思想方法的升華。但本文闡述的初中數學思想主要指轉化思想、數形結合思想、分類討論思想、函數思想、集合思想等通俗易懂的數學思想，有利于學生深刻理解相應的公式、定義、法則和定理等內容。

二、初中數學思想的比較常見類型及其應用

1.巧用數與數轉化思想，輕松找到解決問題的捷徑

在初中數學課堂教學中，為了幫助學生攻克一些比較復雜的題目，教師可以通過數與數的轉化過程，引導學生找到解決具體問題的途徑，這就是數與數的轉化思想，它的具體表現包括三個方面：一是把所學的新問題轉化為原來已經掌握的問題;二是把比較復雜的問題轉化為通俗易懂的問題;三是當新問題用難以理解時，就通過構建新的研究方式解決。

【教學案例1】? 現有兩個多邊形的邊數之比是1∶2，它們的內角和度數之比是1∶3，求這兩個多邊形的邊數分別是多少？

筆者在引導學生解題時，先讓他們通過仔細閱讀后分析，當時大部分學生采取列方程的方法解答此題：先設一個多邊形的邊數是n，另一個多邊形的邊數是2n，然后根據題意，并應用多邊形內角和公式得出方程：3（n-2）·180°=（2n-2）·180°，最終通過比較繁瑣的途徑解答了問題。因此，我積極引導學生應用轉化思想完成解題：只有從多邊形的邊數之比與度數之比之間的關系思考入手，才能把度數之比轉化為邊數之比，從而比較輕松地解決問題。即：從“n 邊形的內角和=（n-2）·180°”公式中，當找到求比值之時，就可以約去180°這個公因數。因此，這個問題就變成：“現有兩個多邊形的邊數之比是1∶2，若邊數都減少2 時，則其邊數之比是1∶3，求這兩個多邊形的邊數分別是多少？”由于靈活應用了轉化思想，許多學生在草稿紙上迅速得出結論，一個多邊形的邊數是：2×2=4，另一個多邊形的邊數是2×3+2=8或4×2=8。類似的解題方法充分體現了數與數的合理轉化思想，為學生提供了比較輕松的解題途徑。

2.應用函數與方程思想，以達觸類旁通之目的

無論是函數，還是方程，既是重要的數學概念，又是重要的數學思想。所謂函數思想，就是指就應用變化和運動的理念，仔細觀察、縝密分析和科學研究具體問題中的數量關系，也就是通過具體函數的形式，巧妙地把數量關系展示出來，從而找到解決問題的具體辦法;而方程思想的本質就是把所探究問題的中的相等關系轉化為方程式或者方程組等數學模型，最終順利地解決問題。

【教學案例2】關于x的方程2kx2-2x-3k-2=0的有兩個根，其中，一個根大于1，一個根小于1，問：實數k的取值范圍是多少？

筆者在幫助學生解答此題時強調：解答這一習題時，假如通過方程的根求解，那計算量就很大，計算過程也比較繁瑣，往往出現解題錯誤的現象。因此，一定要立足于函數方程思想，只有從以下形式轉化為一元二次不等式進行求解，才能取得事半功倍的效果：

設y=2kx2-2x-3k-2，根據題意得：k≠0.①當k>0時，二次函數y=2kx2-2x-3k-2與x軸的交點位于點（1，0）的兩側，則當x=1時，y<0即2k-2-3k-2<0，并且這個函數圖象的開口方向向上;②當k<0時，二次函數y=2kx2-2x-3k-2與x軸的交點位于點（1，0）的兩側，則當x=1時，y>0即2k-2-3k-2>0，并且它的圖象開口方向向下。最后，由①②得出如下結論：k·（2k-2-3k-2）<0.即k2+4k>0，∴k>0或k<-4。

3.強化數形結合思想，培養學生的創新思維能力

在初中數學課堂教學中，教師既可以把數量關系的問題轉化為圖形的性質進行探究，也可以把圖形的問題轉化為數量關系的問題解決，這種圖形的性質與數量關系有機的方法就是數形結合思想，這與新課標倡導的“運用圖形形象地描述問題，利用直觀來進行思考”有異曲同工之妙。

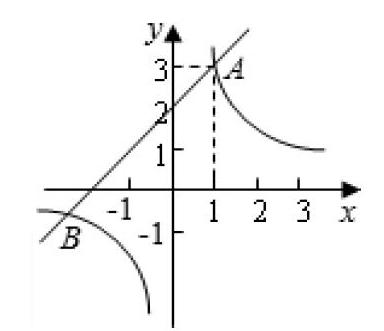
【教學案例3】? 如下圖所示，已知一次函數y=x+m的圖像（m為常數）與反比例函數y=k/x的圖像（k≠0）相交于點A（1，3）。

①問：這兩個函數的解析式以及圖像的另一個交B的坐標。

②結合上述圖像計算出函數值y1>y2的自變量的取值范圍。

筆者在引導學生解答此題時進行如此分析：為了求出函數解析式，可以采取點轉化為數的辦法，即：把點A（1，3）代入相應的函數關系式后得出：m=2，k=3;但最終找到兩個函數圖像的另一交點B的坐標，只有先解答出兩個函數聯立成的方程組，才能實現數轉化為點的目的，即：計算出點B（-3，-1），這樣的解題過程就是充分體現數形結合（轉化）思想，促使學生理解了抽象的方程組解就是在平面直角坐標系中兩個圖像交點的坐標。同時，再讓學生根據圖像寫出函數值y1>y2的自變量的取值范圍時，可以采取由形轉化為數來完成，最終得出函數值y1>y2，即：假如圖像處于平面直角坐標系范圍內，那么其直線一定處于雙曲線的上方位置，最后得出自變量x正確的取值范圍：-3

數學思想猶如天上的繁星，浩瀚無窮，神秘莫測。我們一定要與時俱進，開拓創新，繼續實踐與研究數學思想方法，讓初中數學思想之花在課堂教學中綻放光芒。