基于插值DFT相位差的VDES信號頻偏估計算法

史 珂，馬社祥，孟 鑫

（天津理工大學 a.電氣電子工程學院；b.海運學院，天津 300384）

2013年，為了解決AIS數據鏈路擁堵問題［1］，國際海上助航與燈塔聯合會（IALA）首次提出了VDES（VHF data exchange system，VDES）的概念。VDES是由船舶自動識別系統（automatic identification system，AIS）、應用特定消息（application specific messages，ASM）以及甚高頻數據交換（VHF data exchange，VDE）所組成的集成系統，其中VDE分為VDE地面（船和船，船和岸臺）和VDE衛星上下行鏈路。VDES可以提供相比AIS更高速和更大容量的數據交換，并且可以在全球范圍內通用。在VDES系統中，一般采用的低軌道衛星高度在600～1 000 km，運行速度為7.5 km／s，VDES信號的最大多普勒頻偏約為±4 kHz。頻偏值的存在將直接影響接收機解碼的正確性，為了減小信號頻移造成的影響，提出對接收信號進行頻偏估計與校正，從而確保信息的準確傳輸［2］。2015年10月，國際電信聯盟無線電通信第5研究組建議VDES采用ITU-RM.2092-0［3］：在VDE-SAT下行鏈路中，可采用QPSK調制，其傳輸速率為9.6 kbit／s。

Rife算法是Rife等利用DFT最大和次大兩根譜線幅度，插值計算后得到頻偏估計值［4］。Rife算法公式簡單易于實現，但存在較大缺點：算法為有偏估計，且在噪聲影響下，當信號頻偏接近DFT量化頻點時，頻偏相對偏差較小，可能會出現插值方向相反的情況，從而造成估計性能急劇惡化。Quinn算法中，Quinn同樣利用最大和次大幅度的兩根DFT譜線，但其插值公式利用的是兩根譜線的相位信息，算法在相對偏差較小時也不會出現插值方向錯誤問題，可避免頻偏估計性能在某些點急劇惡化，但此方法計算量略大［5］。鄧振淼等［6］提出改進后的Rife算法，可解決Rife算法估計性能急劇惡化的問題，但代價是算法的運算量和時延劇增，且需要較長的數據長度。劉渝［7］提出一種綜合利用DFT相位和插值估計信號頻偏的算法，該算法估計精度較高且復雜度低，但存在相位模糊問題。為解決該問題，齊國清等提出了利用DFT最大譜線相位差的頻偏估計算法，該方法通過計算兩段DFT譜線峰值處的相位差完成頻率估計，消除了相位模糊，與插值算法相比，該算法僅對其一半長度的信號做DFT運算。但在噪聲影響下，該算法有兩個缺點：一是當輸入信號頻偏發生變化時，用來估計頻偏的DFT譜線可能會逐漸偏離實際信號頻偏點，導致最大譜線位置發生誤判使得頻偏估計性能變差；二是該算法在低信噪比下對頻偏相對偏差非常敏感，而DFT最大譜線對應的頻偏值與實際頻偏的偏差是不可控因素，導致算法的頻偏估計性能不穩定［8］。葉展等針對第1個缺點做出了改進，通過對分段后的信號引入一定頻偏，避免兩段信號同時出現DFT最大譜線的誤判［9］。

本文針對DFT相位差算法的第2個缺點進行改進，在計算相位差之前，首先對頻偏相對偏差進行預估計，預估計時使Rife算法和Quinn算法相結合，綜合兩種插值算法的優點后得到偏差估計值，然后補償進信號中消除頻偏相對偏差的影響，最后可獲得穩定且精確的頻偏估計值。理論分析和計算機仿真結果表明，本文算法對相對偏差不敏感，頻偏估計性能穩定，且算法信噪比閾值較低，估計精度接近克拉美羅界。

1 信號模型

VDE-SAT下行鏈路中信號的調制方式為QPSK調制，鏈路中存在大范圍的時延和頻偏。本文重點討論頻偏估計問題，故假設在接收端進行載波同步處理前，接收信號已經完成了定時同步［10-12］，并且經過系統均衡［13-14］，均衡后的信號近似符合加性高斯白噪聲條件，碼間干擾可忽略。為精確分析噪聲對信號的影響，下文將信號在有噪聲和無噪聲環境的表達式分別表示出來。假設信號不受噪聲影響，接收信號可以表示為

對于接收信號x（t），采用數據輔助下的頻偏估計方法：利用特征碼元（接收端已知）構建再調制信號，將再調制信號取共軛后與接收信號相乘，可得：

式中：z（t）為無噪聲條件下去調制后的信號；*表示取共軛運算。

信道引入加性高斯白噪聲后，接收信號可以表示為

u（t）為獨立同分布的零均值復噪聲信號，方差為σ2。

在高信噪比時，信號可近似為［15］

去調制后為r（t），r（t）為加性高斯白噪聲信道條件下去調制后的信號。

2 DFT相位差分法

2.1 假設信號不受噪聲影響

對z（t）進行采樣，信號持續時間為T，采樣點為N，采樣后為

將z（n）分成前后兩個等長的序列z1（n）和z2（n），表達式為

分別對兩序列做N／2點DFT得：

其中Ak和φk分別為Z1（k）的幅度項和相位項，表達式分別為：

由式（9）可知，Z1（k）和Z2（k）的幅度Ak完全相同，Ak最大值處對應的離散頻率點記為k0，可知k0＝［fd T／2］（［·］表示取整），此時可得頻偏粗估計值為

其中Δf＝2／T為DFT的頻率分辨率。

φ1和φ2分別為Z1（k）和Z2（k）在最大幅度譜線處的相位，定義二者的差值Δφ為

則有：

由式（12）得

則最后的頻偏估計值為

2.2 噪聲對頻偏估計的影響分析

上文中，在高斯白噪聲條件下對接收信號去調制后得：

為分析噪聲對頻偏估計精度的影響，將式（16）還原成：

其中，u（t）為復高斯白噪聲，均值為0，方差為其前N／2點采樣序列為

此時對r1（n）作N／2點DFT，其中采樣后白噪聲序列u1（n）的DFT變換可以視作若干隨機變量的線性組合，其每項DFT系數仍為隨機變量，所以u1（n）的DFT變換仍可看做隨機序列。定義u1（n）的N／2點DFT變換為

其中b和φu分別為U1（k）的幅度項和相位項，二者均為隨機變量。且U1（k）的均值E［bexp（jφu）］為0，方差Var［bexp（jφu）］為Nσ2u／2。

r1（n）的N／2點DFT為

由式（20）可得R1（k）的幅度項和相位項分別為：

在較大的DFT輸出信噪比下，在幅度峰值點k0處的φR（k）可近似表示為

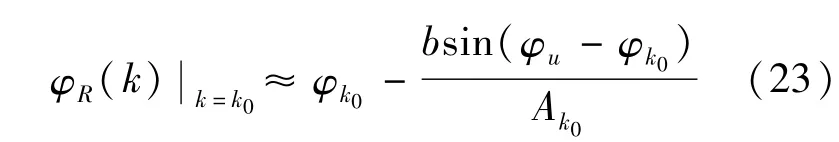
由

可得

當N足夠大時，由式（9）可知幅度峰值Ak0可近似為

其中sinc（x）＝sin（πx）／（πx），δ＝k0-fd T／2，表示相對頻率偏差。

將式（26）代入式（25）可得

由式（14）可知fδ估計的方差為

由于DFT輸出信噪比一般較大，此時DFT幅度峰值譜線位置k0估計錯誤造成的誤差可以忽略，fd的估計誤差主要取決于fδ的估計誤差，則：

對DFT相位差分法進行仿真分析，設置信號持續時間T＝0.005 s，頻率分辨率為2／T＝400 Hz，碼元周期Tb為1／4 800 s，采樣后的樣點數為N＝128個，設置頻偏為fd＝9.5Δf＝3 800 Hz。對頻偏采用500次重復Monte Carlo模擬，頻偏估計的性能采用歸一化均方誤差（MSE）來衡量。由式（29）可得：信號頻偏與相對偏差δ密切相關，當信號頻偏正好位于幅值最大譜線上時，δ為0，此時估計誤差最小；當信號頻偏位于兩條離散譜線中間時，δ為±0.5，此時估計誤差最大。使信噪比SNR為2 dB，δ取值為（-0.5，0.5），圖1為不同δ取值下的估計誤差曲線，頻偏估計的性能采用歸一化均方誤差（MSE）來衡量：

其中P為Monte Carlo循環次數。

圖1 不同δ取值下的估計誤差曲線

在實際應用中，DFT最大譜線對應的頻偏值與實際頻偏的偏差δ是不可控因素，其取值在（-0.5，0.5）范圍是隨機的。為降低δ的不確定性對頻偏估計性能的影響，需要對DFT相位差分算法做出改進。

3 改進的頻偏估計算法

3.1 對偏差δ的預估計

要消除δ對頻偏估計的影響，考慮利用插值算法對相對偏差δ進行預估計。Rife算法提出利用信號頻譜的最大和次大幅度的兩根譜線估計相對偏差δ0［4］，從而推算出頻偏估計值，其偏差δ0估計公式為

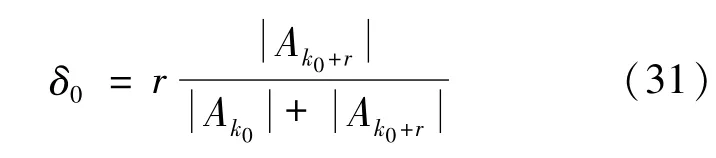
當Ak0＋1＜Ak0-1時，r＝-1；當Ak0＋1＞Ak0-1時，r＝1。該算法的優點在于插值公式簡單，易于計算，但在噪聲影響下，當較小時，可能會出現插值方向相反的情況，從而造成較大的頻偏估計誤差。

其中：Re（·）為取復數實部運算，R（k）為式（20）的R1（k）。分別計算若δ1與δ2都大于0，則δ0＝δ1；否則δ0＝δ2。與Rife算法相比，Quinn算法在較小時不會出現插值方向錯誤問題，可避免較小時估計誤差增大，但此方法計算量略大。

綜上，可設定δ的門限值為δR，當δ≤δR時，使用Quinn算法預估δ0；當δ＞δR時，使用Rife算法預估δ0。由上文分析可知，門限δR的取值與信噪比和δ值密切相關。圖2為不同信噪比下的Rife算法與Quinn算法的估計性能對比曲線，估計性能采用δ的歸一化均方誤差（MSE）來衡量。

其中P為Monte Carlo循環次數。由圖2可知：隨著信噪比增大，兩種算法的估計性能曲線越來越相似，門限δR的取值也越來越小，說明在信噪比較大時不需要設置門限。

VDES接收信號的信噪比一般為0～20 dB，設置門限值時主要考慮0 dB時的誤差。由圖2可知，在信噪比為0 dB時兩曲線交點在0.2～0.3范圍，設置門限值δR∈（0.2，0.3），SNR＝0 dB，圖3為不同門限值下的估計性能對比。

圖2 不同信噪比下的Rife算法與Quinn算法的估計性能對比

圖3 不同門限值下的估計性能對比

由圖3可知，信噪比為0 dB時，算法的估計性能在門限范圍δR∈（0.2，0.3）內相差很小。在VDES信號頻偏估計中，為了保證δ0預估計的正確性，且使計算量適當，可將門限值設置為0.2。

3.2 基于插值DFT相位差的頻偏估計算法步驟

改進后算法的流程如圖4所示，可具體描述如下：

步驟1將r（n）分成前后兩個等長的序列r1（n）和r2（n），分別對兩序列做N／2點DFT，設置門限值δR。

步驟2利用Rife算法計算δ0，若δ0≤δR，繼續步驟3，否則繼續步驟4。

步驟3利用Quinn算法計算δ0。

步驟4將r1（n）和r2（n）頻移δ0個量化單位后，利用頻譜細化［16-17］方法分別計算R1（k0＋δ0）和R2（k0＋δ0）。

步驟5分別計算R1（k0＋δ0）和R2（k0＋δ0）的相位，得到二者相位差Δφ。

步驟6頻偏估計值為

綜上，對相對偏差δ進行預估計后，δ的取值不會對頻偏估計性能產生影響，即改進后的算法對DFT幅值最大譜線對應的頻偏值與實際頻偏的偏差并不敏感，由此提高了算法的穩定性和精確度。

圖4 基于插值DFT相位差的頻偏估計算法流程

4 改進算法的仿真分析

將門限值δR設置為0.2，信噪比SNR 為2 dB，δ取值范圍為（-0.5，0.5），采用500次重復Monte Carlo模擬，將改進后算法與原DFT差分算法及其頻偏估計的克拉美羅界（CRLB）進行對比，仿真結果如圖5所示。由圖5可看出：與原算法相比，改進后的DFT插值相位差分算法的頻偏估計性能受δ影響不大，在δ取值范圍內估計誤差基本保持穩定，且接近克拉美羅界。

圖5 不同δ取值下的頻偏估計性能對比

為進一步驗證本算法改進后的性能，在頻偏分別為f1＝9.5Δf＝3 800 Hz（δ＝0.5）和f2＝9.1Δf＝3 640 Hz（δ＝0.1）時，對本文算法和原DFT算法在不同信噪比下的頻偏估計性能進行仿真，其結果如圖6所示。4條曲線依次為原算法與本文算法分別在δ為0.5和0.1時的頻偏估計性能曲線，使其與算法的克拉美羅界（CRLB）相對比。由圖6可以看出：在低信噪比下，受噪聲影響兩種算法的頻偏估計性能都高于CRLB。對比原算法在δ為0.5和0.1時曲線可知該算法受到δ取值影響較大，δ為0.5時的頻偏估計性能明顯與δ為0.1時相差較大；而改進后的算法對δ并不敏感，兩種δ取值下的頻偏估計性能相似，并且在較大信噪比下的仿真結果非常接近CRLB。

圖6 兩算法的頻偏估計性能對比

由式（29）可知，頻偏估計性能與DFT點數N密切相關，在頻偏為fd＝3 800 Hz，N分別為64、128、256、512的情況下對本文改進算法的頻偏估計性能進行仿真，結果如圖7所示。可看出DFT點數N越大，頻偏估計性能越好，但DFT點數的增加也伴隨著計算量的增加，在實際應用中，應綜合考慮所需的精確度與計算的復雜度來選取N值。

圖7 不同N取值下的頻偏估計性能對比

5 結束語

本文主要針對基于插值DFT相位差的VDES信號的頻偏估計算法進行研究。首先推導驗證了DFT相位差算法中噪聲對估計精度的影響，發現在低信噪比下算法估計性能對頻偏相對偏差δ非常敏感，然后針對該缺點綜合利用兩種插值方式對δ進行預估計，將估計值δ補償入信號后再計算相位差，最后得到頻偏估計值。與原DFT算法相比，本文算法不受頻偏相對偏差δ影響，算法的估計性能穩定，可適用于各種頻偏，且估計精度接近CRLB，說明用于VDES系統是可行的。