雙軸連續旋轉調制捷聯慣導系統大失準角初始對準技術

許昊天，趙春柳，邵海俊，繆玲娟

（1.北京理工大學自動化學院，北京100081；2.國家國防科技工業局軍工項目審核中心，北京100039）

0 引言

由于隱蔽性好、自主性強，捷聯慣導系統（Strapdown Inertial Navigation System，SINS）可在各種復雜環境下工作，已成為了一種被廣泛應用的系統［1?2］。由于SINS的導航誤差會隨時間增加而積累，因此SINS在長時間條件下的導航精度會有所降低。目前，許多先進的SINS均采用了旋轉調制技術來補償慣性器件的輸出誤差［3］。為了解決單軸旋轉調制技術無法調制旋轉軸方向上器件誤差的問題，許多學者對雙軸旋轉調制技術展開了研究［4?5］。

初始對準是慣性導航的核心技術之一，其對準精度直接決定了后續導航的精度［6?7］。在SINS初始對準的研究中，通常將誤差模型看作經典的線性模型，這種線性模型是在慣導系統粗對準后姿態誤差角較小的情況下獲得的。在工程實際中，由于基座晃動及各種干擾的存在，粗對準后的姿態誤差角并非小角度，基于小失準角的線性誤差模型無法滿足現實應用的要求，基于大失準角捷聯慣導系統的誤差模型和非線性估計方法得到了許多學者的關注［8?9］。

近年來，平方根容積Kalman濾波算法（Square?root Cubature Kalman Filter，SCKF）已可以很好地解決SINS大失準角初始對準問題，但其需要對噪聲的統計特性有準確了解，否則可能出現很大的狀態估計誤差，甚至導致濾波發散［10］。Sage?Husa算法能夠實時在線估計系統的噪聲統計特性，從而顯著提高濾波算法的自適應能力［11?13］，但其只能被應用于線性系統中。因此，本文將SCKF算法與Sage?Husa算法相結合，提出了采用QR分解來完成對噪聲協方差的平方根矩陣進行估計的ASCKF算法，從而提高了非線性濾波算法的自適應性，同時避免了傳統Sage?Husa SCKF算法在非線性較強的情況下易出現系統過程噪聲協方差矩陣與量測噪聲協方差矩陣不正定的情況。

1 坐標系定義

以下為本文所涉及到的坐標系：

（1）地心慣性坐標系（i系）

原點選為地心，zi軸沿地球自轉方向，xi軸、yi軸位于赤道平面內，xi軸從地心指向春分點，yi軸與xi軸、zi軸構成右手坐標系。

（2）地球坐標系（e 系）

原點位于地心，ze軸沿地球自轉方向，xe軸指向赤道平面與格林尼治經線的交點，ye軸與 xe軸、ze軸構成右手坐標系。

（3）地理坐標系（t系）

原點位于載體的質心處，xt、yt、zt分別指向東向、北向、天向。

（4）導航坐標系（n 系）

本文選取地理坐標系為導航坐標系。

（5）載體坐標系（b 系）

與載體固連，其原點位于載體重心，xb軸、yb軸、zb軸分別指向載體的右、前、上方向。

（6）慣性測量單元坐標系（s系）

原點位于慣性測量單元（IMU）的重心，3個坐標軸的指向為慣性傳感器的敏感軸，初始時刻s系坐標軸指向與b系一致。對于單軸旋轉式慣導系統而言，轉動方向為繞方位軸旋轉；對于雙軸旋轉式慣導系統而言，轉動方向為繞方位軸和橫滾軸旋轉。

2 旋轉調制機理及誤差分析

旋轉式SINS采用傳統SINS的解算算法對慣性測量單元的輸出信息進行導航解算，從而得到導航結果。導航解算過程如圖1所示。

旋轉式SINS的基本工作原理與傳統SINS一致，只是在SINS的基礎上添加了旋轉平臺。旋轉式SINS的位置誤差方程與傳統SINS一致，在此不再列出。其姿態和速度誤差模型為

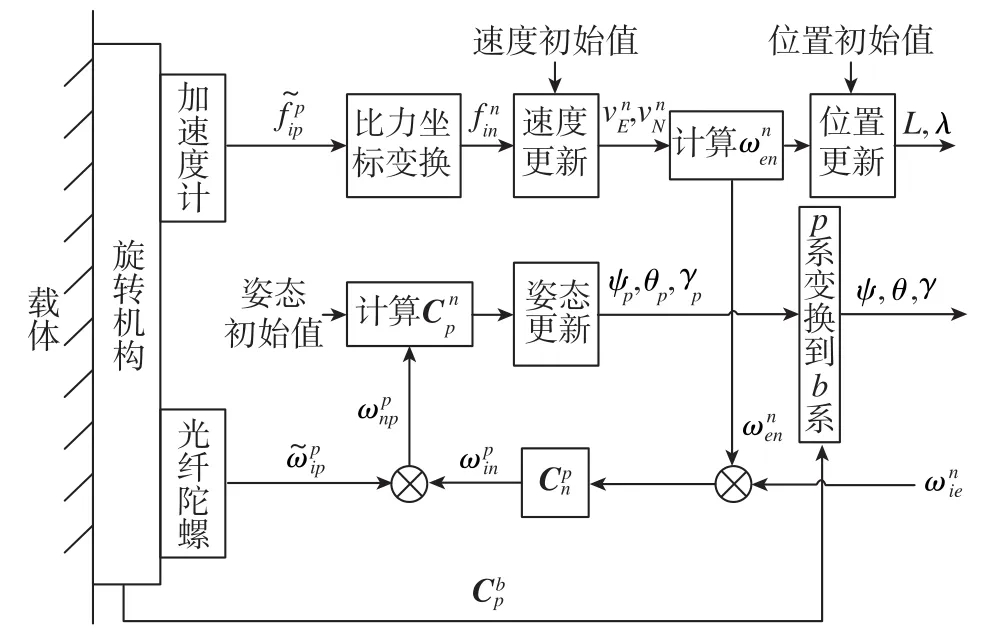
圖1 導航解算方案Fig.1 Scheme of navigation solution

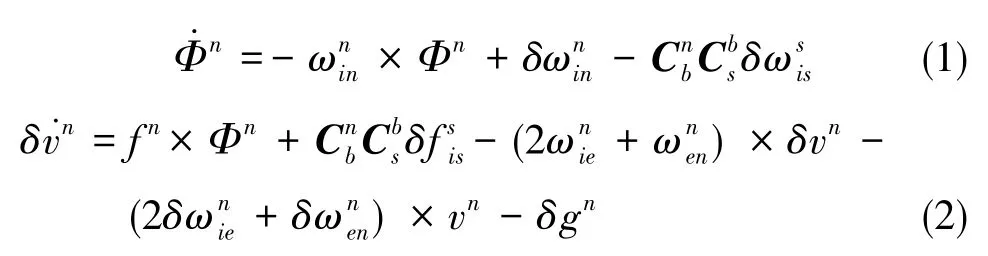
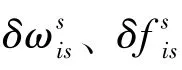
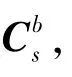
假設在任意時刻t，IMU繞任意旋轉軸的旋轉角度為α（t），則s系到b系的變換陣為

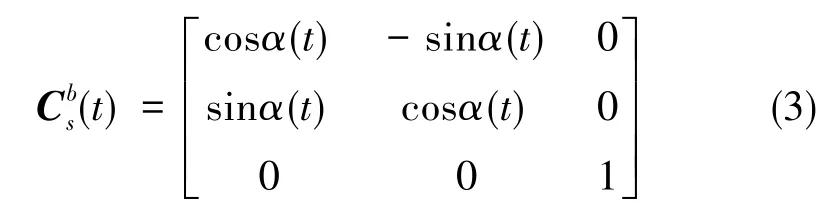
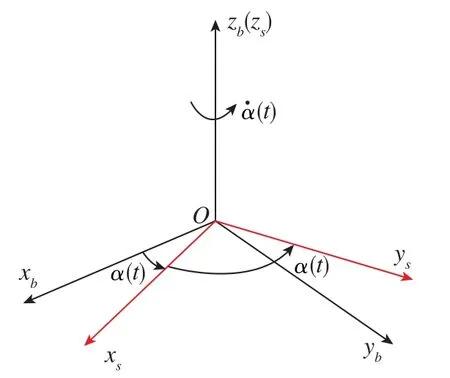
圖2 b系與單軸旋轉s系之間的關系Fig.2 Relationship between b-system and uniaxial rotation s-system

在旋轉式捷聯慣導系統中，慣性器件安裝于平臺上，測量的是s系相對于i系的運動。因此，慣性器件的信號輸出可以表示為

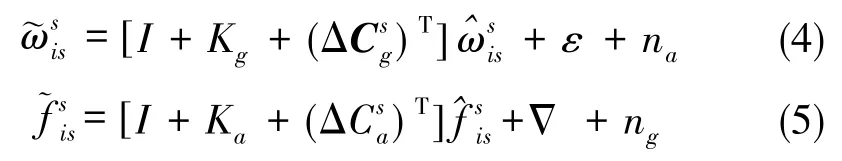
忽略二階及二階以上小量，由式（4）、式（5）可以推出，陀螺和加速度計的輸出誤差為

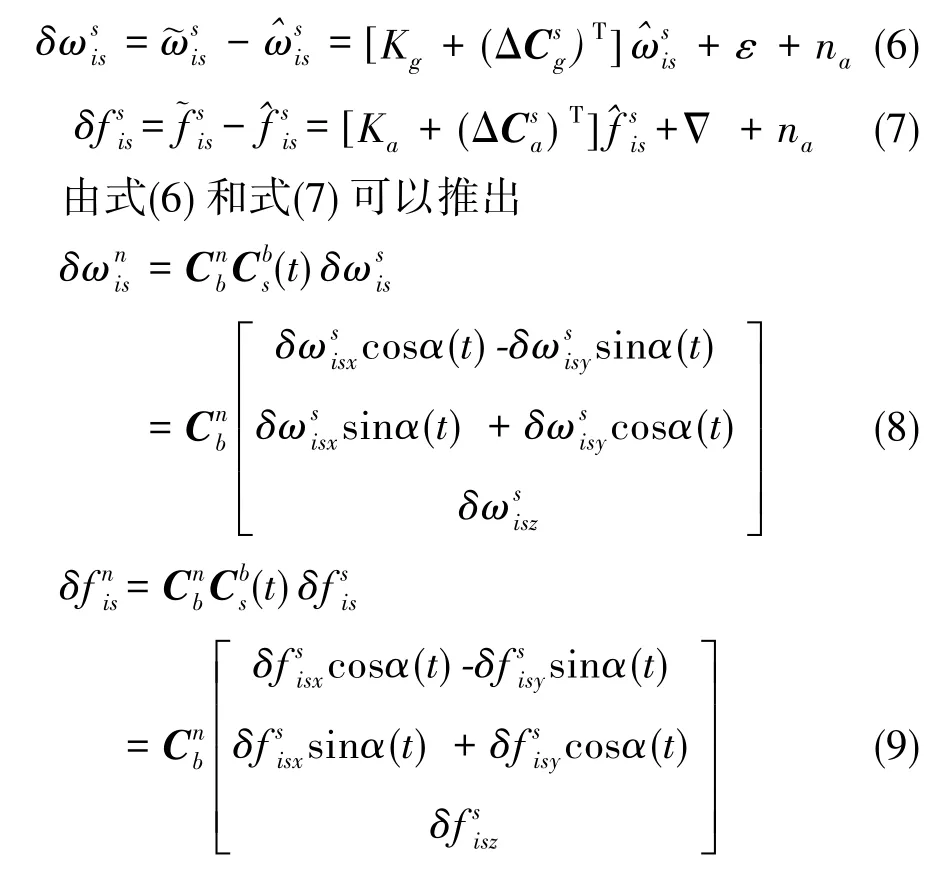
當系統進行旋轉調制時，與旋轉軸垂直的兩個軸上的慣性器件誤差會被調制為正余弦形式，而在旋轉軸方向上的誤差則不被調制。將式（8）、式（9）在一個旋轉周期內進行積分，由于與旋轉軸垂直方向的誤差是正余弦形式，因此其積分結果為0，從而可抑制系統誤差，而在旋轉軸方向上的誤差則按照原來的規律傳播。因此，單軸旋轉式捷聯慣導系統只能抑制與旋轉軸相垂直的兩個軸向上的誤差，而無法減少旋轉軸上的誤差。若想抑制三個軸上的誤差，可采用雙軸旋轉調制方案。

3 雙軸旋轉調制方案設計

本文采用十六次序雙軸連續旋轉方案，具體轉位方案與文獻［14］相同。

設慣性測量單元的旋轉速率為Ω，次序1、3、6、8繞方位軸轉動，在載體坐標系O?xbyb平面內呈現出正、反一周的變化規律。設每一次序轉動時間為T/2，則在轉動過程中陀螺常值漂移在載體坐標系x軸的投影積分為

由式（10）和式（11）可知，次序 1、3、6、8 在轉動過程中累積的常值誤差為0，即

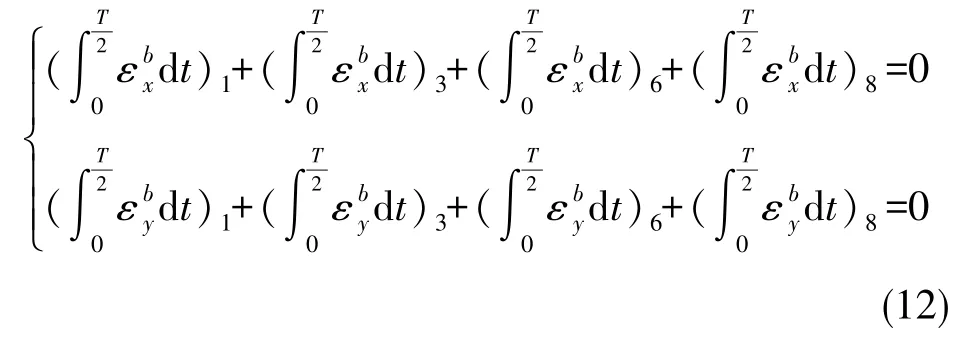
根據類似的計算方式，次序2、4、5、7繞橫滾軸轉動，在轉動過程中在載體坐標系O?xbzb平面內同樣呈現出正、反一周的變化規律，累積的常值誤差為0，即

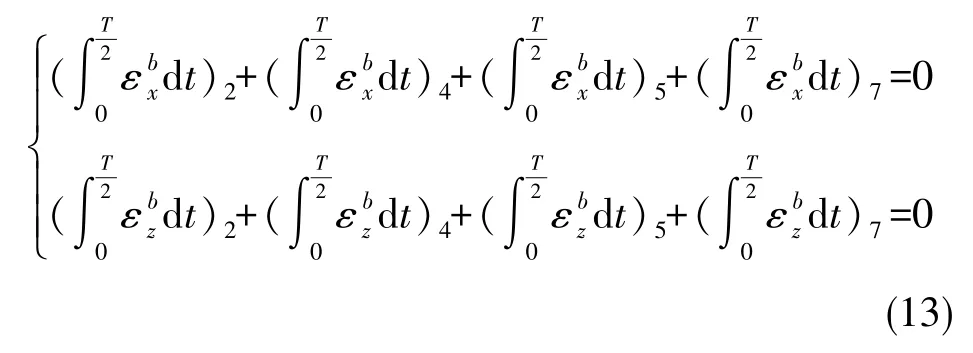
次序9、11、14、16繞方位軸轉動，在轉動過程中在載體坐標系O?xbyb平面內呈現出正、反一周的變化規律，累積的常值誤差為0，即

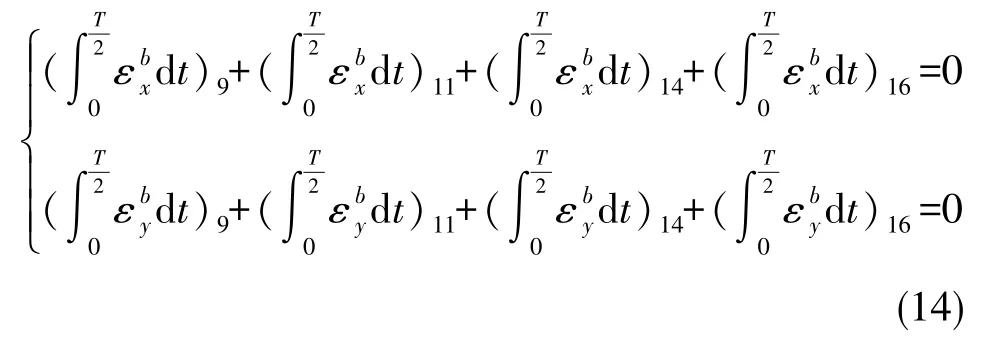
次序10、12、13、15繞橫滾軸轉動，在轉動過程中在載體坐標系O?xbzb平面內呈現出正、反一周的變化規律，累積的常值誤差為0，即

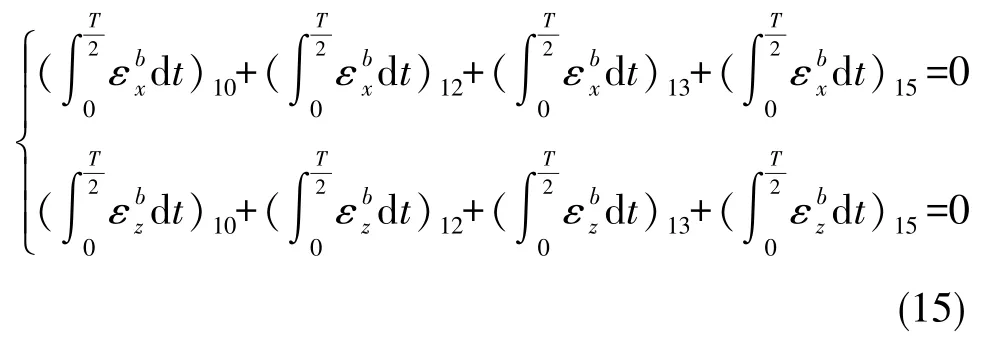
由式（10）～式（15）可知，陀螺的常值漂移被完全調制。加速度計的常值偏值調制過程與陀螺類似，因此本文選擇的十六次序雙軸連續旋轉方案可將慣性器件的常值誤差完全調制，進而避免了誤差的積累。

文獻［14］表明，在采用十六次序雙軸旋轉調制方案后，慣性器件標度因數誤差的影響與傳統SINS一致，標度因數誤差不會引起導航坐標系下東向角誤差，但會由于標度因數誤差與地球自轉角速度分量耦合而引起北向和天向角誤差，并隨時間積累。安裝誤差會與地球自轉角速度分量耦合引起隨時間積累的姿態角誤差，本文限于篇幅不再對這兩項誤差進行計算。

4 ASCKF算法

4.1 非線性誤差模型

在靜基座初始對準中，由于在實際的工程環境中存在基座晃動及各種干擾，粗對準后的姿態誤差角比較大，此時無法使用傳統的線性濾波方程進行精對準。嚴恭敏［9］針對這一問題研究了捷聯慣導系統非線性誤差模型，設導航坐標系（n系）經歷三次轉動到達計算導航坐標系（n′系），三次轉動的角度分別為 αx，αy，αz。令 α＝［αxαyαz］T，有

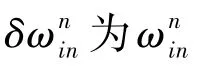
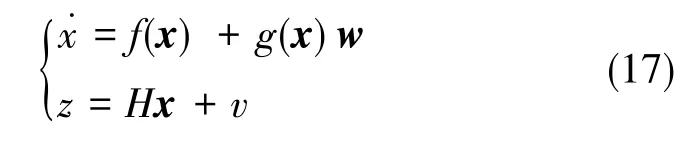
該狀態方程和量測方程為慣導系統誤差模型的通用表達式，后文運用該表達式進行了濾波對準。

4.2 SCKF算法

平方根容積Kalman濾波算法（SCKF）由于濾波精度高、穩定性強，在非線性系統中的應用較為廣泛。因此，本文選擇該算法在靜基座條件下進行初始對準。

設非線性系統離散化的狀態方程與量測方程為

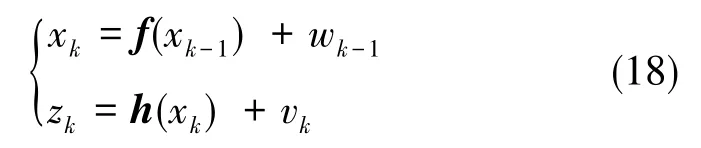
式（18）中，f為非線性狀態轉移矩陣，h為線性量測矩陣，wk-1、vk為互不相關的零均值Gauss白噪聲，方差分別為Qk-1、Rk。SCKF算法的計算步驟如下所示：

（1）初始化，給定均值和協方差

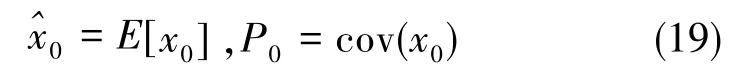
計算球容積點和權值，即有

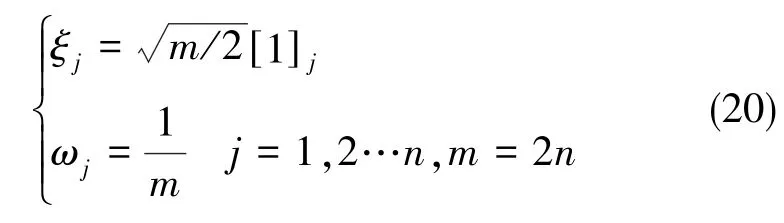
式（20）中，［1］＝［I，-I］，I為 n 維單位方陣，［1］j表示取［1］的第 j列。

（2）時間更新

SCKF算法借鑒了平方根濾波的思想，避免了復雜的矩陣求逆和分解運算，直接以協方差平方根矩陣的形式在相鄰時刻間進行遞推更新，能夠有效提高濾波的計算效率和數值穩定性。

4.3 傳統的Sage-Husa SCKF算法

SCKF算法在用于大失準角初始對準時需要對噪聲的統計特性有準確了解，否則可能出現很大的狀態估計誤差，甚至導致濾波發散。王思思［10］提出的Sage?Husa SCKF算法利用Sage?Husa噪聲估計器對系統噪聲的均值qk及觀測噪聲的均值rk進行了在線估計，并對系統過程噪聲協方差矩陣Qk、觀測噪聲方差矩陣Rk進行了實時修正，從而使得SCKF算法具有了自適應性。

假設非線性系統中的時變噪聲wk、vk分別為互不相關的Gauss白噪聲，過程噪聲的協方差Qk為非負定矩陣，量測噪聲的協方差Rk為正定矩陣。在估計時變噪聲的統計特性時，應當注重最新數據對系統的影響，逐漸遺忘陳舊數據。傳統的Sage?Husa SCKF算法可總結如下：

（1）初始化

按照式（19）、式（20）完成參數初始化過程，并對Q0、R0、q0、r0賦予初始值。

（2）狀態估計

按照式（21）～式（38）進行 SCKF 濾波估計。

（3）噪聲參數估計

按照式（39）～式（42）對噪聲參數進行更新。

系統過程噪聲的均值為

通過在SCKF中加入Sage?Husa時變噪聲統計估計器，可以有效估計出當前時刻的系統過程噪聲與量測噪聲，減少陳舊數據對濾波過程的干擾，從而提高濾波算法的自適應性。

4.4 ASCKF算法

由于傳統的Sage?Husa SCKF算法在系統階次較高或系統非線性較強的情況下易出現系統過程噪聲協方差矩陣Qk與量測噪聲協方差矩陣Rk不正定的情況，進而易導致濾波算法無法繼續進行計算。因此，本文提出了改進Sage?Husa SCKF算法，即AS?CKF算法。該算法利用QR分解來完成對噪聲協方差平方根矩陣的估計，避免了傳統Sage?Husa SCKF算法在非線性較強的情況下易出現系統過程噪聲協方差矩陣與量測噪聲協方差矩陣不正定的情況，從而可配合SCKF算法完成自適應濾波過程。

針對式（18）所描述的系統，本文提出的ASCKF算法的具體過程如下所示：

1）設定初值，并設定 SQ，0＝chol（Q0）、SR，0＝chol（R0）。其中，chol為矩陣的 Cholesky 分解。

2）按照式（21）～式（38）進行 SCKF 濾波估計。

3）對噪聲統計特性進行估計。

觀測噪聲協方差的平方根為

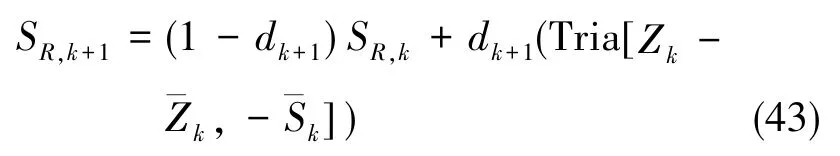
系統過程噪聲協方差的平方根為

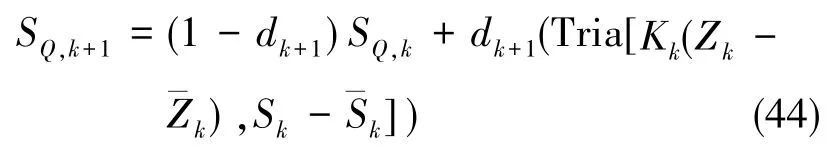
將改進的 ASCKF 算法通過式（43）、式（44）計算噪聲協方差的平方根矩陣，并直接將式（43）、式（44）分別帶入式（31）、式（25）中，從而避免了傳統 Sage?Husa SCKF 算法使用式（41）、式（42）進行計算時易出現的矩陣非正定問題，以及由此導致的式（27）、式（33）無法進行計算的問題。在下文的仿真分析中，將運用ASCKF濾波算法對雙軸旋轉式捷聯慣導系統進行非線性初始精對準。

5 仿真結果與分析

5.1 SINS與旋轉式SINS初始對準結果對比

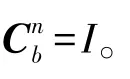
雙軸旋轉式SINS靜基座的初始對準結果如圖3所示，單軸旋轉式SINS靜基座的初始對準結果如圖4所示，傳統SINS靜基座的初始對準結果如圖5所示。

分別對三種慣導系統的初始對準結果進行20次Monte Carlo仿真實驗，取各次實驗的姿態角誤差的算數平均值作為對準精度的評價指標，其結果如下：

1）雙軸旋轉式SINS的方位角誤差為0.177°，俯仰角誤差為0.006°，橫滾角誤差為-0.012°；

2）單軸旋轉式SINS的方位角誤差為0.219°，俯仰角誤差為0.011°，橫滾角誤差為-0.014°；3）SINS的方位角誤差為 0.374°，俯仰角誤差為0.016°，橫滾角誤差為-0.019°。

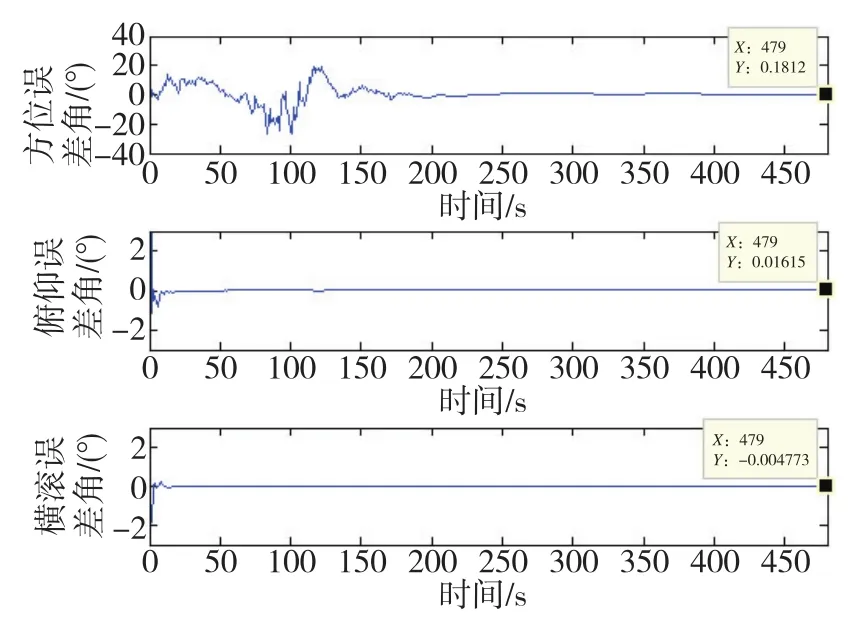
圖3 雙軸旋轉式捷聯慣導系統SCKF算法的初始對準結果Fig.3 Initial alignment of SCKF algorithm for biaxial rotary SINS

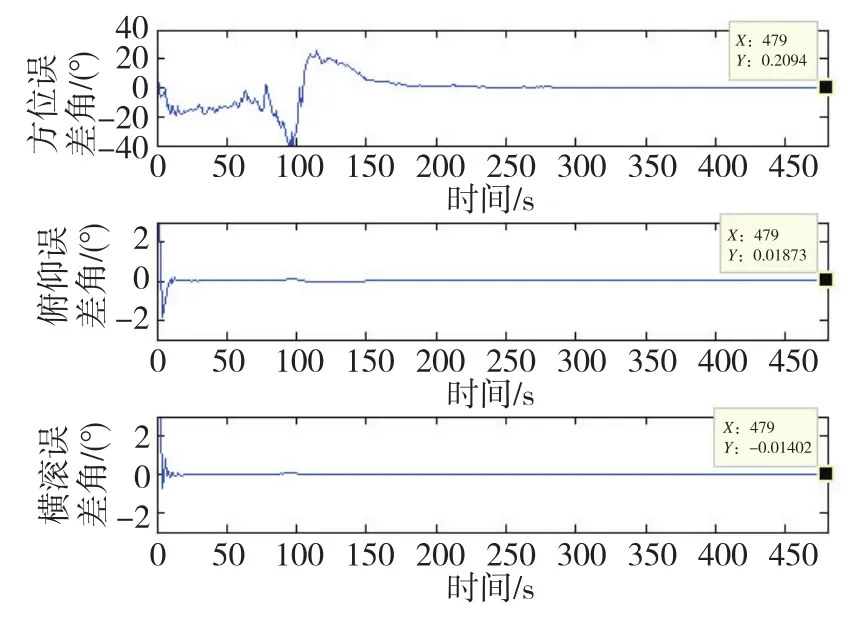
圖4 單軸旋轉式捷聯慣導系統SCKF算法的初始對準結果Fig.4 Initial alignment of SCKF algorithm for single axis rotary SINS

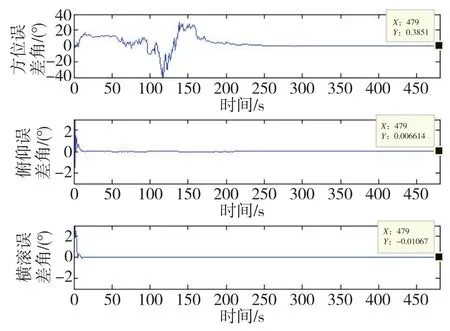
圖5 捷聯慣導系統SCKF算法的初始對準結果Fig.5 Initial alignment of SCKF algorithm for SINS

顯然，單軸旋轉式SINS靜基座的初始對準精度與雙軸旋轉式SINS基本相當。但由于對準時間有限，并且考慮到系統非線性對誤差收斂速度的影響，單軸、雙軸旋轉式捷聯慣導系統均未能讓方位誤差角收斂到一個較小的范圍。傳統SINS靜基座初始對準精度不如兩種旋轉式SINS。

5.2 ASCKF算法的仿真結果與分析

為了驗證在噪聲模型不確定情況下的ASCKF濾波算法具有良好的自適應能力，本節采用十六次序雙軸連續旋轉方案，并通過實驗模擬了噪聲發生突變的情況。實驗仿真的初始條件在5.1節的基礎上，在300s后觀測噪聲的方差增大了100倍。采用SCKF濾波算法的靜基座初始對準結果如圖6所示，采用ASCKF濾波算法的靜基座初始對準結果如圖7所示。

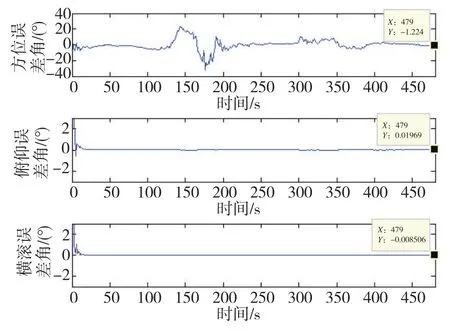
圖6 雙軸旋轉式SINS SCKF濾波算法在噪聲變化環境下的初始對準結果Fig.6 Initial alignment of biaxial rotary SINS SCKF algorithm in noisy changing environment

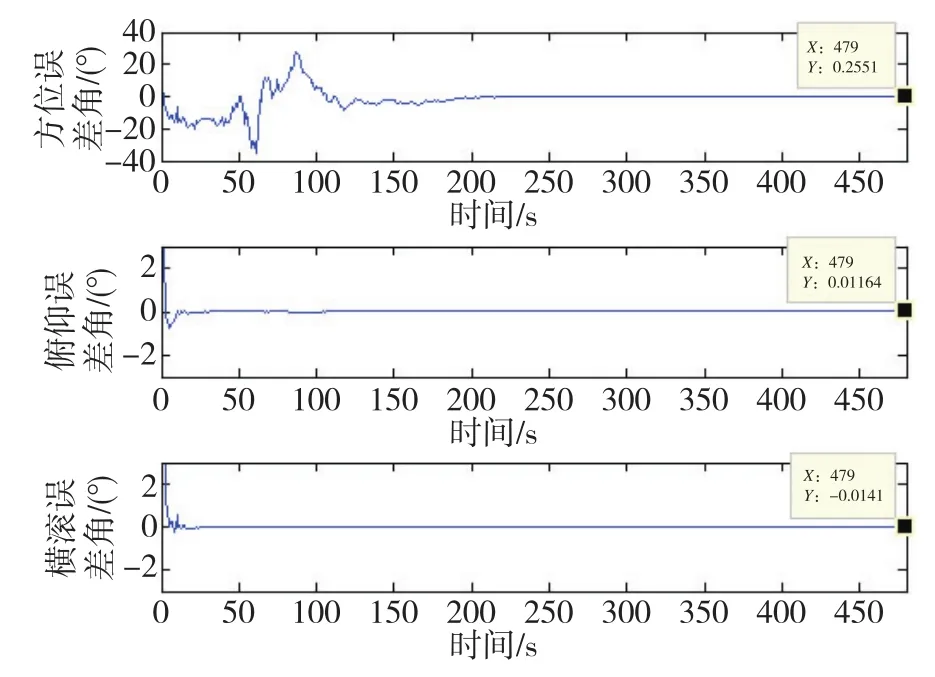
圖7 雙軸旋轉式SINS ASCKF濾波算法在噪聲變化環境下的初始對準Fig.7 Initial alignment of biaxial rotary SINS ASCKF algorithm in noisy changing environment

分別對兩種濾波方案進行20次Monte Carlo仿真實驗，取各次實驗的姿態角誤差的算數平均值作為對準精度的評價指標，結果如下：

1）雙軸旋轉式SINS采用SCKF算法在噪聲統計特性發生突變的情況下進行大失準角初始對準的方位角誤差均值為-1.528°，俯仰角誤差均值為0.016°，橫滾角誤差均值為-0.018°。

2）雙軸旋轉式SINS采用ASCKF算法在噪聲統計特性發生突變的情況下進行大失準角初始對準的方位角誤差均值為0.307°，俯仰角誤差均值為0.011°，橫滾角誤差均值為-0.015°。

顯然，在噪聲模型發生變化的情況下，采用傳統的SCKF濾波方法會使方位角的對準精度明顯降低，而ASCKF算法則具有很好的自適應性，可以很好地被應用于噪

6 結論

本文采用通過理論推導更好地抑制旋慣導系統的非SCKF算法，并法的基礎上，提出了一種ASCKF濾波算法。該算法采用QR分解來完成對噪聲協方差的平方根矩陣的估計，從而避免了傳統Sage?Husa SCKF算法所面臨的所估噪聲協方差矩陣非正定所帶來的問題。最后，通過仿真驗證了在觀測噪聲發生突變的情況下ASCKF濾波算法具有良好的自適應性。