基于陀螺系的速率偏頻慣性測量組合標定方法

江一夫，陳 勇

（中國航天科技集團第十六研究所，西安710100）

0 引言

通常情況下，激光陀螺和加速度計敏感軸的方向與捷聯慣測組合基準面所確立的坐標軸方向是大致平行或正交的。針對這類直裝捷聯慣導系統，主要有三類標定方法，包括分立式標定方法［1］、基于誤差解耦的迭代式擬合估計方法［2?4］及基于零速量測的 Kalman濾波標定方法［5?7］。目前，這些方法都趨于成熟，能較好地解決慣性測量組合的定期維護問題。

為了能夠基于一個轉位機構使得三只激光陀螺同時敏感到旋轉角速率，速率偏頻慣導系統中的慣性儀表往往采取斜置的安裝方式［8］。早在20世紀80年代，國外便開始研制速率偏頻激光陀螺系統［9?11］，但未見慣性儀表標定方面的相關文獻。在國內，文獻［12］提出了結合光學測量標定陀螺安裝誤差角的方法，這種方法利用速率偏頻轉臺自身的旋轉角速率對陀螺刻度系數和常值漂移進行了簡易標定。文獻［1］提出了一種斜裝慣性儀表的標定算法，這實際上是一種簡單的、基于殼體基準系的分立標定方法。文獻［13］提出了速率偏頻系統的Kalman濾波標定方法，其原理與直裝系統類似。文獻［14］提出了一種基于模值不變原理的標定方法，但是其陀螺零偏和加速度計標定流程繁瑣而復雜。

對于斜裝系統，常規標定方法均是理論可行的。但在工程實際應用中發現，斜裝系統存在其獨有的、不可忽視的問題，即標定結果存在較大的激光陀螺標度因數誤差。本文以分立式標定為例，分析了造成陀螺標度因數標定誤差的原因，認為速率偏頻系統獨有的傾斜安裝方式造成了旋轉軸與陀螺敏感軸之間的大角度安裝偏差，導致常規標定方案無法完全激勵出陀螺標度因數誤差。

為了解決傳統標定方法不適應斜裝慣導系統的問題，本文提出了一種新的基于陀螺系的系統級整機標定方法。由于陀螺敏感軸具有較高的穩定性，相對于以加速度計作為參考坐標系的標定方法，該方法確保了導航過程輸出空間姿態基準的絕對穩定性，同時有利于提高激光陀螺安裝角的標定精度和標定穩定性。

1 速率偏頻慣導系統的模型

為了能夠基于一個旋轉臺使三軸陀螺都能敏感到旋轉角速率，從而實現速率偏頻，系統中的激光陀螺需采用如圖1所示的傾斜安裝方式。

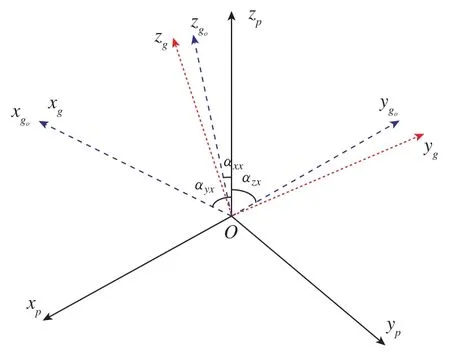
圖1 速率偏頻激光陀螺慣導系統的安裝方式示意圖Fig.1 Mounted scheme of rate-bias laser-gyro inertial navigation system

定義g系為由三軸陀螺敏感軸構成的非正交系，定義 go系（Oxgoygozgo）為陀螺正交參考坐標系，xgo軸與陀螺敏感軸xg重合，ygo軸在xgyg平面內，zgo軸與xgo軸、ygo軸構成正交系。在實際過程中，非正交系g與go系之間存在小角度的安裝誤差。定義p系為轉位機構的臺面坐標系，zp軸與轉位機構的旋轉軸重合，xp軸與xgo軸在轉臺臺面上的投影重合，yp軸與zp軸、xp軸構成正交系。

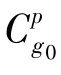
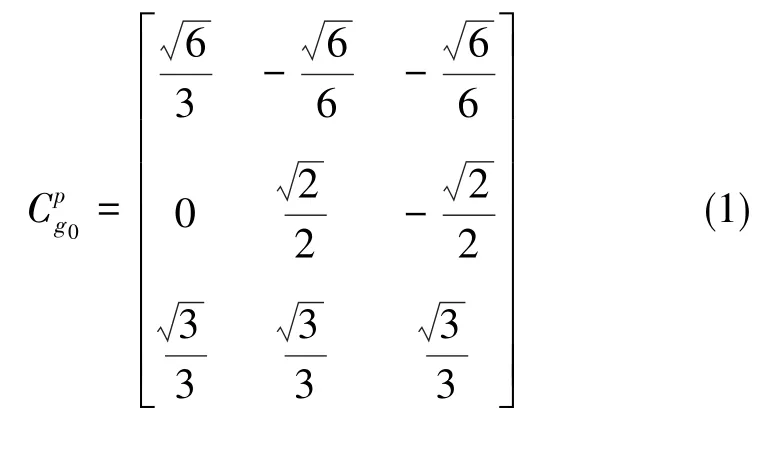
2 常規標定方法存在的問題

針對斜裝系統，一些學者提出直接采用分立式標定方法。其中，激光陀螺采用速率標定方式，其標定模型如下

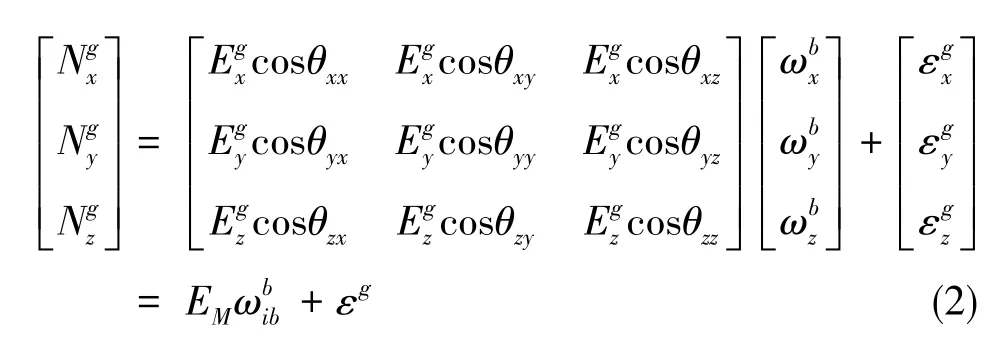
由于b系是正交的，故式（2）標定矩陣每行的模值為對應的標度因數［15］，以x軸為例有

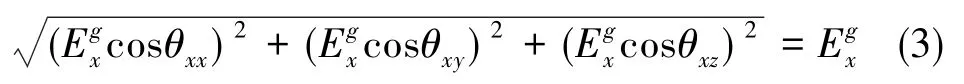
分立標定均以外界物理基準坐標系作為參考坐標系，但是由于加工問題，捷聯慣組的標定工裝或其本身的定位面存在不正交誤差。同時，在速率標定三軸依次朝上的過程中，由于旋轉式慣導系統轉軸間隙的存在，三軸慣性儀表系相對外部基準坐標系發生了變化，這實際上帶來了較大的安裝角誤差。

假設 θxx不存在誤差，而 θ′xy和 θ′xz都存在 10″的誤差，三者的理想值為54.7356°，θxy為114.0948°，θxz為 135.0000°。根據式（3），可估算出將存在4.2×10-5的誤差。當系統為直裝時，θxx的理想值為0°，θxy的理想值為90°，θxz的理想值為90°，上述安裝角誤差僅引起了2.4×10-9的標度因數誤差。因此，這種速率標定方法無法準確標定激光陀螺標度因數的現象是斜裝速率偏頻系統所獨有的。

同樣，利用迭代式擬合估計和Kalman濾波標定方法計算斜裝系統的標定參數，發現激光陀螺標度因數存在2×10-5左右的誤差，這與直裝慣導系統的多位置翻滾標定方案無法充分激勵斜裝系統中的陀螺標度因數誤差而導致標度因數誤差和安裝角誤差無法實現準確分離有關。而一般系統級標定方法的安裝角標定精度較高，因而相對分立式標定方法，系統級標定中的標度因數誤差較小，但是仍然不能滿足使用要求。為了解決這個問題，本文提出了一種新的基于陀螺系的系統級標定方法。

3 基于陀螺系的標定方法

3.1 三軸陀螺標定方法

假設陀螺的輸出模型如式（4）所示

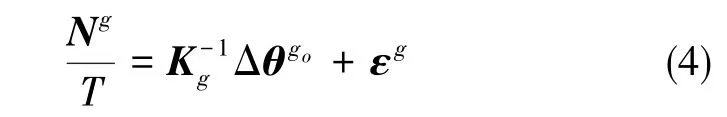
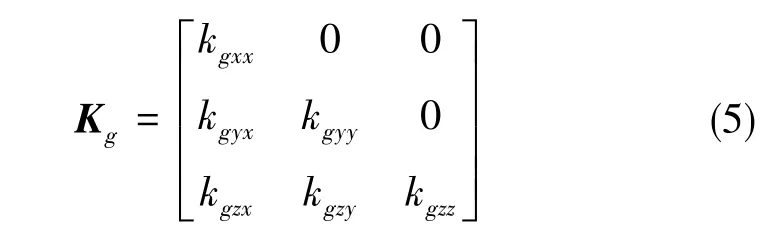
由于正反轉消除了陀螺零偏和地球自轉的影響，對正反轉n圈過程的陀螺輸出進行積分并相減，得到的旋轉矢量模值大小必然為4nπ，即有

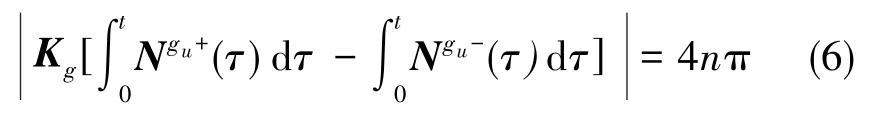
采用解非線性方程組的最優化算法［16］，通過多次迭代運算可求得Kg中的所有參數。為了減少計算量，本文采用文獻［17］中的最小二乘算法，令

在Kg已知的條件下，利用最小二乘算法可以計算出εgu。

3.2 三軸加速度計標定方法

以陀螺正交系go建立加速度計標定模型

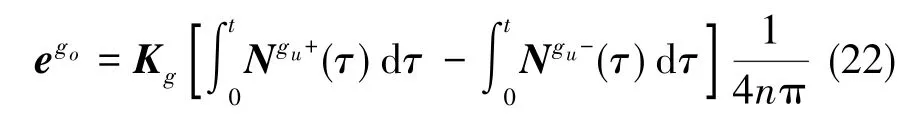
使IMU外箱體三軸分別朝上和朝下，可以得到如式（22）所示的6組18個方程，通過最小二乘算法可以解出三軸加速度計需要標定的所有參數。

4 試驗結果及驗證分析

采用陀螺零偏穩定性優于 0.003（°）/h、加速度計偏置約為50μg的單軸旋轉速率偏頻慣導系統進行標定試驗。以單陀螺在陀螺測試工裝上的標定結果作為參考基準，X、Y、Z 3個90型激光陀螺的標度因數參考值分別為：2.14426163＾/（″）、2.14510797＾/（″）和 2.14456973＾/（″）。其中，＾/（″）表示脈沖每角秒。

4.1 常規標定方法的試驗結果

分立標定以殼體定位面確定的坐標系為輸出參考系。其中，陀螺采用速率標定方法，通過調整慣組的擺放方向使其沿慣組殼體坐標軸各正反旋轉一整周，標定過程的陀螺原始采樣脈沖經數字濾波后的變化曲線和標定結果如圖2和式（23）所示。

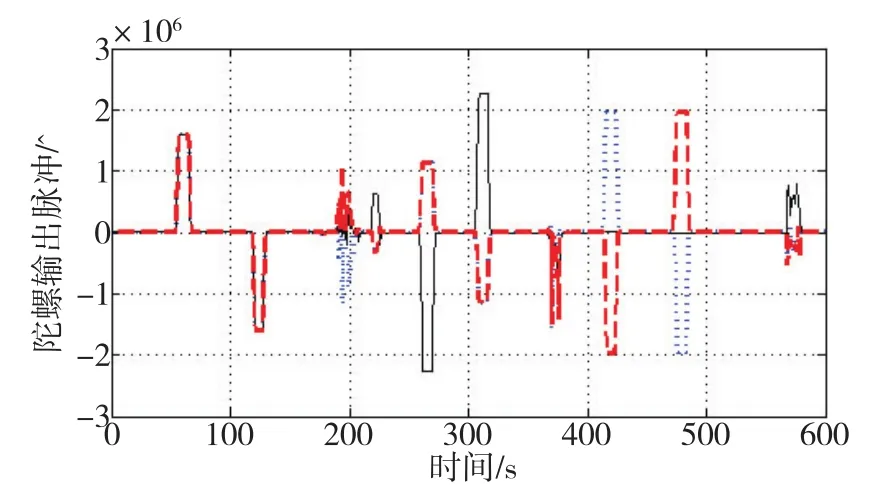
圖2 速率標定過程的激光陀螺輸出脈沖Fig.2 Output pulse of laser gyros during rate-calibration test

采用文獻［1］中的計算方法，對矩陣EM的每行求模值，可得到3個陀螺的標度因數［2］，分別為：2.14398708＾/（″）、2.14510855＾/（″）、2.14482703＾/（″）。

采用系統級多位置Kalman濾波標定方法對斜裝速率偏頻系統進行標定，加速度計的原始脈沖輸出如圖3所示，標定結果如式（24）和式（25）所示。

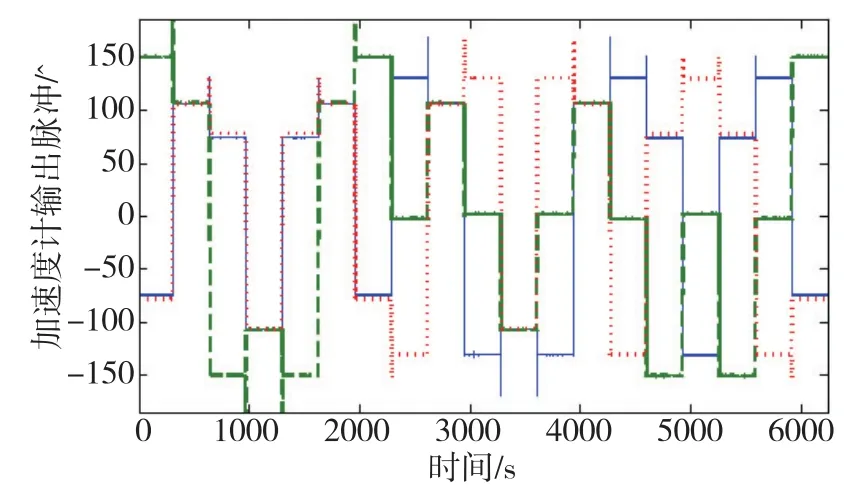
圖3 速率偏頻系統多位置翻滾標定中的加速度計輸出脈沖Fig.3 Output pulse of accelerometers during multi-position systematic calibration test

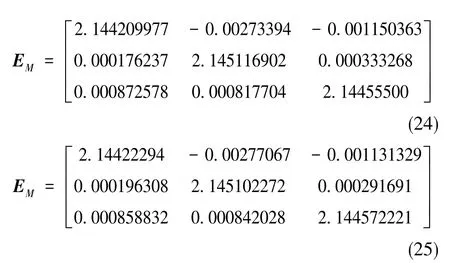
將用常規標定方法進行的三軸陀螺標度因數的標定結果及誤差進行整理，可得如表1所示的結論。

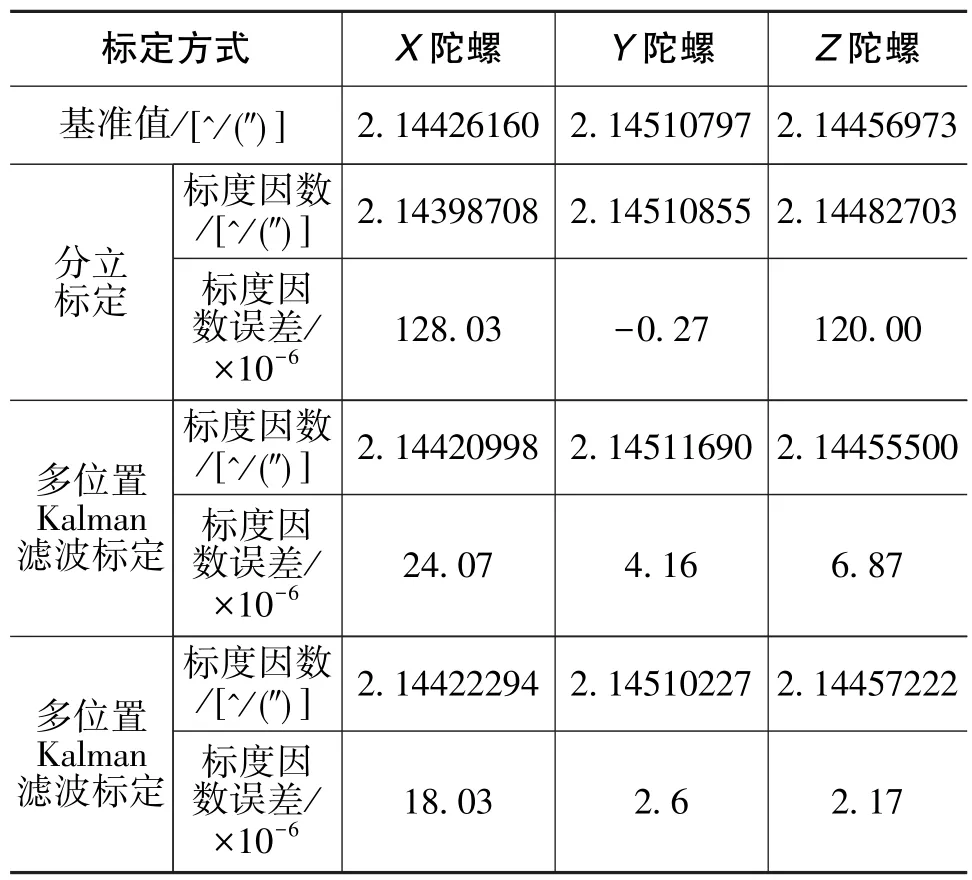
表1 常規標定方法的陀螺標度因數結果及誤差Table 1 Calibration result and error of tradition calibration method

4.2 陀螺系標定方法的試驗結果

為了驗證本文所提出的陀螺系標定方法的有效性和長間隔時間下的標定穩定性，在7個月的時間內進行了4次標定，其標定結果如表2所示。

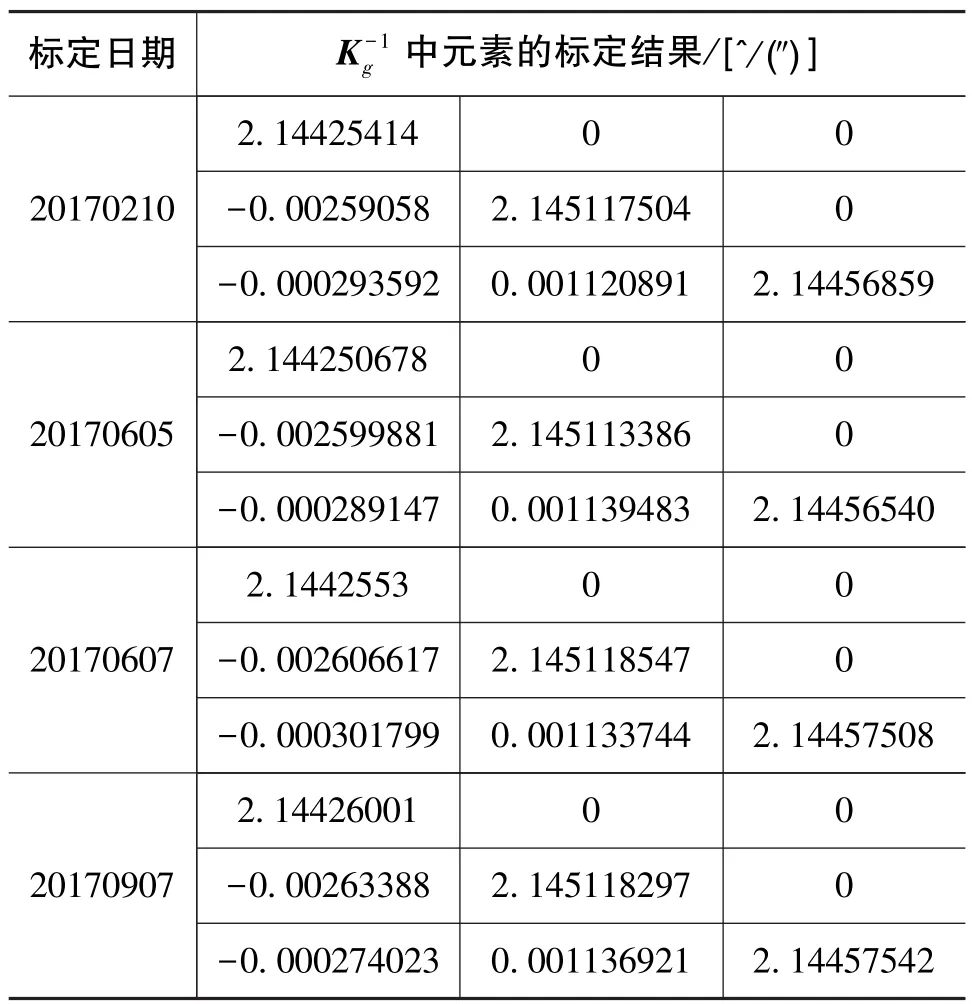
表2 陀螺系標定方法的標定結果Table 2 Calibration results of gyro-axis-based calibration method

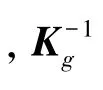
4.3 試驗分析和結論

從表1中常規標定方法的試驗結果可以看出，以單陀螺測試結果為基準，在分立標定中，X陀螺存在約1.28×10-4的標定誤差，Z陀螺存在約1.2×10-4的標定誤差，遠遠超出了高精度導航系統的允許范圍。同時，試驗結果也驗證了前文的理論分析結論，即分立標定中安裝角誤差會引起較大的陀螺標度因數誤差。而常規直裝慣導采用的多位置翻滾Kalman濾波標定方法在速率偏頻系統中仍然不能完全解決陀螺標度因數精確標定的問題。從表1的結果可以看出，X陀螺的標度因數誤差并未完全收斂，而是存在約2×10-5的誤差，仍然不能滿足高精度慣導系統的使用要求。

針對本文提出的基于陀螺系的標定方法，從表2的結果可以看出，以單陀螺測試結果為基準，7個月內的4次標定的陀螺標度因數的最大誤差為5.2×10-6，重復性優于4×10-6，陀螺安裝角標定重復性優于4.2″，說明了該標定方法的有效性和相對較高的長時間穩定性。

5 結論

本文從理論分析和工程實際出發，說明了常規標定方案無法實現速率偏頻系統激光陀螺標度因數精確標定的問題，認為引起該現象的深層原因主要在于速率偏頻系統獨有的傾斜安裝方式，其小量安裝角誤差仍然會引起較大的標度因數誤差。為了解決該問題，本文提出了一種新的基于陀螺系的標定方法，主要利用旋轉矢量模值不變原理及旋轉矢量與重力矢量之間的關系，來實現三軸陀螺和三軸加速度計參數的估計。試驗證明，該方案不但能實現對速率偏頻斜裝慣導系統的精確標定，而且陀螺標度因數和安裝角的標定結果具有相對較高的長時間穩定性，證明了該方案具有較高的工程應用價值。