內聚力模型在復合材料界面層中應用

耿勝彪 沙云東

摘 要：加工制造復合材料時，界面最難控制且大多是最為薄弱的部分，在承受載荷時，界面層處也往往最先出現破壞，從而大大降低了復合材料的強度。因此在進行復合材料細觀模型分析時，界面層不能夠被忽略。界面的強度對整個單胞模型強度的影響非常大，本文通過纖維頂出法計算出復合材料界面層內聚力模型的本構參數，然后分別對代表體積元RVE模型在縱向拉伸載荷和橫向拉伸載荷下做有限元計算，分析界面損傷和基體塑性變形的數值關系，結果表明，復合材料的縱向拉伸強度隨界面強度增加而增加，但到一定程度后影響就變小了，代替的是基體拉伸強度起主要作用。不論界面強度值增加到多大，所得到的復合材料的橫向拉伸強度都永遠低于基體的拉伸強度980Mpa，這充分的說明了復合材料的強度極限是由最最薄弱的部分決定的。本文的研究結論可以為復合材料的制備提供理論參照。

關鍵詞：內聚力模型;界面層;失效模式

0 引言

在對TiC/TC4復合材料應用內聚力模型進行細觀力學模型計算之前，必須先確定界面層的cohesive本構關系。內聚力本構模型的參數是由實驗測得的，但大多數情況下，一些材料的基本力學性能參數是沒有的，此時想要繼續研究，就需要做一些理論推導與假設。本文就是由纖維頂出法測得界面結合強度與界面反應厚度的關系式，然后經過一系列計算，就可以確定界面層內聚力模型本構的基本參數，進而展開后續的分析計算研究。

1 理論分析

1.1 參數的計算

采用纖維頂出法試驗測得SiC/TC4復合材料的界面結合強度可以用下式表示：，其中是纖維與基體之間界面的剪切強度值，H是界面層的厚度。經有限元計算分析，復合材料的界面結合強度與載荷大小的關系為，其中是加載時的最大載荷。

其中K是內聚力本構模型的剛度值，h是薄片試樣的厚度，E是彈性模量，是應力，是應變，是位移。這里假設界面的結合強度等于本構關系中的最大應力取H=1um，E=330Gpa，=6.2N，代入計算，可以求最大應力為102.5Mpa，試件的厚度為0.21mm，位移為0.065um，本構關系=0時對應的位移取0.2um，計算得到斷裂韌性為10.25。這里近似認為張開型斷裂界面的材料屬性與滑開型斷裂相同。得到內聚力本構關系曲線為：

1.2 失效準則的選取

破壞起始是指材料的剛度開始弱化。有多種判定準則，例如最大應變準則、平方應變準則、最大應力準則、平方應力準則等。具體用哪種準則由具體的材料特性而定 ，一般運用較多的是平方應力準則。在下面的討論中用平方應力準則。

2 模型的建立與計算分析

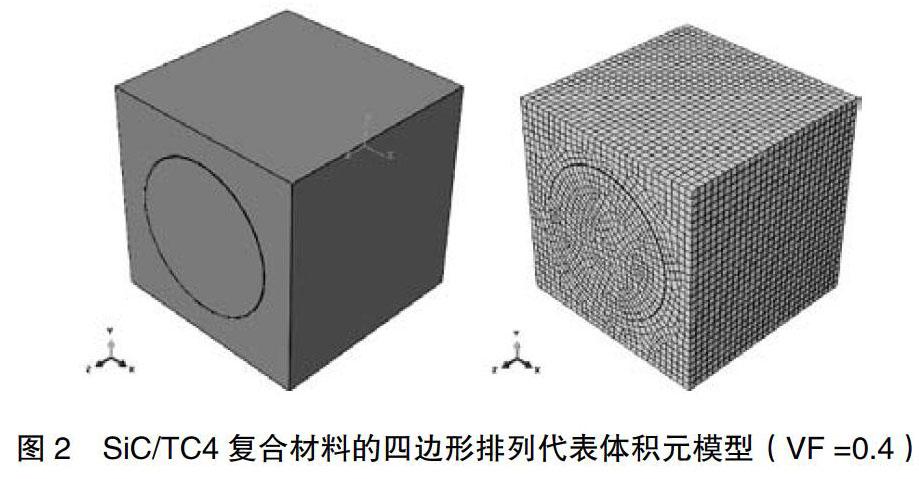
2.1 模型的建立與參數選取

2.2 有限元計算結果分析

2.2.1 縱向拉伸載荷下的應力應變分析

在縱向拉伸載荷下研究不同界面強度復合材料對應的強度極限，分別選用正常的界面強度，0.2和2倍界面強度進行有限元計算分析。

圖中橫軸表示應變，縱軸表示應力。由應力應變曲線可知，隨著界面強度的增大，復合材料的縱向拉伸強度并不會一直增大，當界面強度增大到某一數值之后，界面強度對復合材料強度的影響就不是那么明顯了，這時起主要作用的是基體的拉伸強度。材料剛度隨著界面強度增加而增加，材料的非線性首先在弱界面時出現，原因是界面損傷導致材料的剛度降低。同時界面的強度增強會導致復合材料呈現出一定的脆性，所以在實際的應用中，并不是界面的強度越大越好，應該根據實際的需要選擇合適的界面強度。

2.2.2 不同界面強度下對應的損傷演化分析

圖中橫軸表示應變，縱軸表示損傷百分比。從圖4曲線可以看出，弱界面時，縱向拉伸漸進損傷過程為，界面首先在很小的應變時出現損傷，隨著載荷的不斷增加，界面損傷的百分比數值急速上升，界面的損傷范圍和程度也隨之快速加大。當界面損傷到一定程度時，接著是基體開始出現屈服，隨著載荷的不斷增加，基體的塑性變形也不斷增大。界面的損傷百分比迅速達到1附近，然后基本維持此數值不變，而基體的塑性變形則是隨著載荷的增加而緩慢的上升。

由圖5可知，強界面時界面和基體的損傷曲線走勢很相似，縱向拉伸漸進損傷過程為，基體首先在很小的應變時出現塑性變形，繼續加載，界面也開始出現損傷，然后基體和界面損傷的百分比共同隨著載荷的增加而增加，當應變達到0.02時，基體的塑性變形程度維持在1附近，不再隨載荷的變化而變化，而基體的損傷程度則是在應變達到0.03之后，隨著載荷的增加而緩慢的上升。

2.2.3 單胞模型在縱向拉伸載荷下的受力分析

由上面云圖6可知，在實際的界面強度下，對單胞模型進行受力計算分析，界面處對應的應力，應變，位移均是最大的，說明了對于TiC/TC4復合材料來說，界面處最為薄弱，在加載時，界面處肯定是最先破壞的。同時界面的損傷云圖可以看出，在縱向載荷下，界面的損傷并不是均勻分布的，說明即使是一個單胞，其內部的受力也是十分復雜的。

2.2.4 橫向拉伸載荷下的應力應變分析

在橫向拉伸載荷下研究不同界面強度復合材料對應的強度極限，分別選用正常的界面強度，0.2倍和無限大界面強度進行有限元計算分析。

圖中橫軸表示應變，縱軸表示應力。由應力應變曲線可知，弱界面時，復合材料的橫向拉伸強度緩慢增加，在應力為96Mpa時取得最大值，然后緩慢減小;中強界面時，復合材料的橫向拉伸強度增幅比較明顯，在應力為460Mpa時取得最大值，然后以比較快的速度減小;強界面時，復合材料的橫向拉伸強度迅速增加，在應力為920Mpa時取得最大值，然后迅速減小;同樣當界面強度增大到某一數值之后，界面強度對復合材料強度的影響就不是那么明顯了，這時起主要作用的是基體的拉伸強度。同時還能比較直觀的觀察出，不論界面強度值增加到多大，哪怕是無限大，所得到的復合材料的橫向拉伸強度都永遠低于基體的拉伸強度980Mpa，這充分的說明了復合材料的強度極限是由最最薄弱的部分決定的。縱向對比還可以發現，當基體的強度值固定不變時，界面的結合強度值對復合材料的橫向拉伸強度影響很大。

3 結論

（1）復合材料的縱向拉伸強度隨界面強度增加而增加，但到一定程度后影響就變小了，此時基體的拉伸強度起主要作用。（2）弱界面時，界面的損傷百分比迅速達到1附近，然后基本維持此數值不變，而基體的塑性變形則是隨著載荷的增加而緩慢的上升。（3）強界面時，當應變達到0.02時，基體的塑性變形程度維持在1附近，不再隨載荷的變化而變化，而基體的損傷程度則是在應變達到0.03之后，隨著載荷的增加而緩慢的上升。（4）不論界面強度值增加到多大，所得到的復合材料的橫向拉伸強度都永遠低于基體的拉伸強度980Mpa。（5）基體的強度值固定不變時，界面的結合強度值對復合材料的橫向拉伸強度影響很大。

參考文獻：

[1]蔡杉，李占一，董妍，顏鳴皋等.SiC_Ti_153復合材料界面與性能研究[J].航空材料學報，2006，26（06）：55-59.

[2]朱艷，楊延清，馬志軍，陳彥等.SiC_Ti基復合材料界面反應的熱力學研究[J].稀有金屬材料與工程，2002，31（04）：279-282.

[3]沙云東，賈秋月，駱麗等.連續纖維增強金屬基復合材料渦輪軸結構承扭特性分析[J].航空動力學報，2016，31（06）：1377-1384.

[4]Baik，Kyeong Ho.Tensile failure behavior of SiC/Ti-6Al-4V composites manufactured by plasma spraying route[J].Materials Transactions，2006，47（11）：2815-2820.

[5]Fukumoto，Shinji;Hirose，Akio;Kobayashi，Kojiro F，et al.Effective joint of continuous SiC/Ti-6Al-4V composites by diffusion bonding[J].Composites engineering，1995，5（08）：1081-1089.