一道用微元法求解物理題的推廣
韓福濟
(湖北省武漢市華中科技大學附屬中學 430074)
一、題目及微元法
例1 如圖1(a),一質量為m的均勻閉合細繩套在一光滑鐵圓錐上,鐵圓錐半頂角為α,求解當細繩平衡時,繩中的張力為多少?
分析:細繩在光滑鐵圓錐上的每點受力相同,如以整個細繩為研究對象,則問題變得很難,而將細繩用微元法化為小的微分弧段,也可以認為是質點為研究對象,就可以分析其受力,從而將問題迎刃而解.
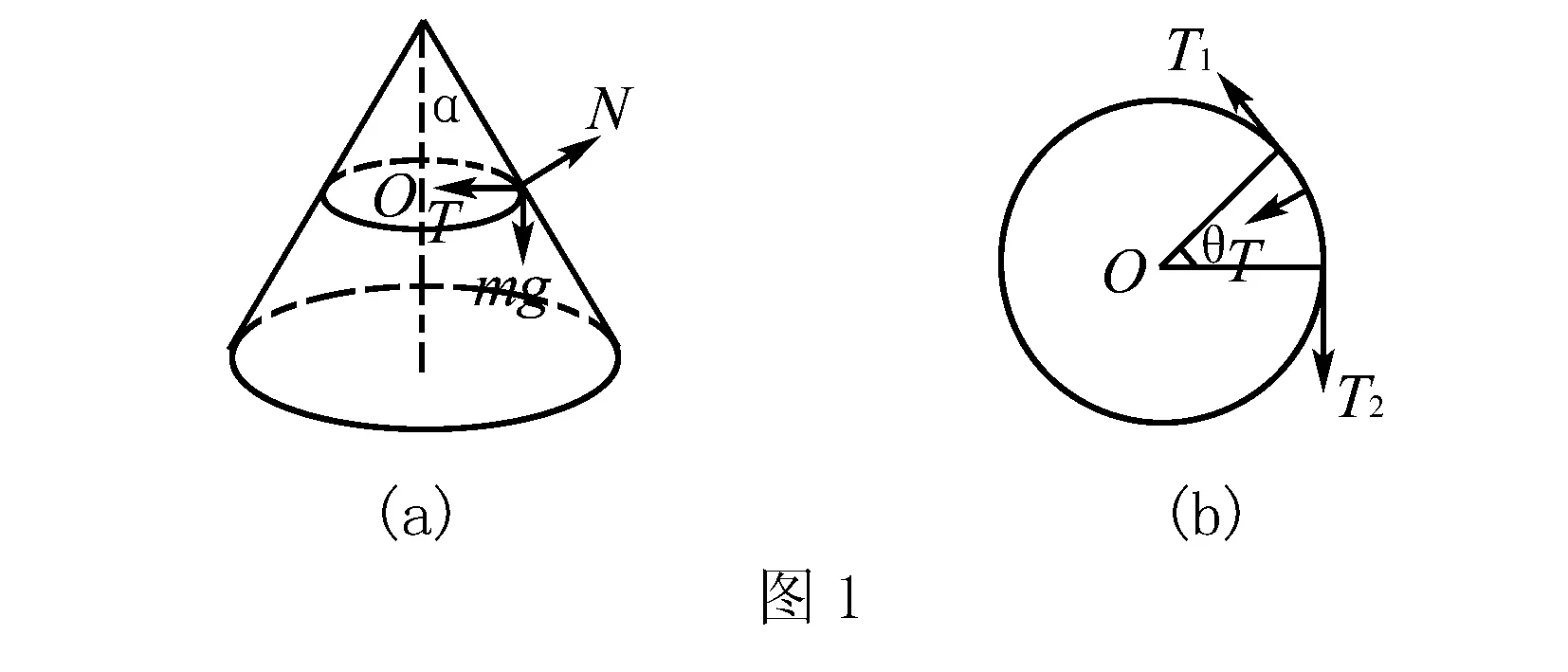
解將細繩劃分為n個小弧段,取其中的一個弧段微元為來研究.
假設繩圈的半徑為R,這個小弧段的圓心角為θ,質量為Δm,微元的受力分析如圖1(b)所示:重力為Δmg,彈力為N,合力為T,有平衡條件得到下列式子:
(1)N·cosα=T,N·sinα=Δmg.
現在設微元弧段的兩個端點的張力分別是T1、T2,并且它們的大小相等,其合力T,方向指向原點O. 由力的分解可知:
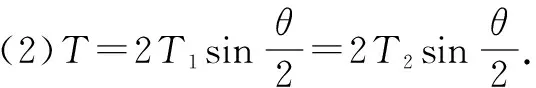
并且由于繩圈是均勻的,所以有
聯立(1)(2)(3)式,得到:
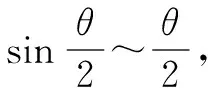
二、將圓錐體推廣為光滑鐵球體
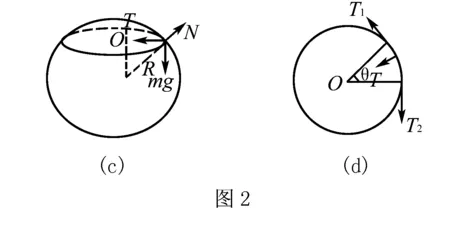
例2 如圖2(c),一質量為m的均勻閉合細繩套在一光滑鐵球體上,鐵球體的半徑為R,繩套的長度為L,且繩套長度小于球的大圓周長. 求解當細繩平衡時,繩中的張力為多少?
分析1 類比于例1,進行分析計算.
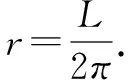
重力為Δmg,彈力為N,合力為T,有平衡條件得到下列式子:
現在設微元弧段的兩個端點的張力分別是T1、T2,并且它們的大小相等,其合力T,方向指向原點O. 由力的分解可知:
并且由于繩圈是均勻的,所以有
聯立(5)(6)(7)式,得到:
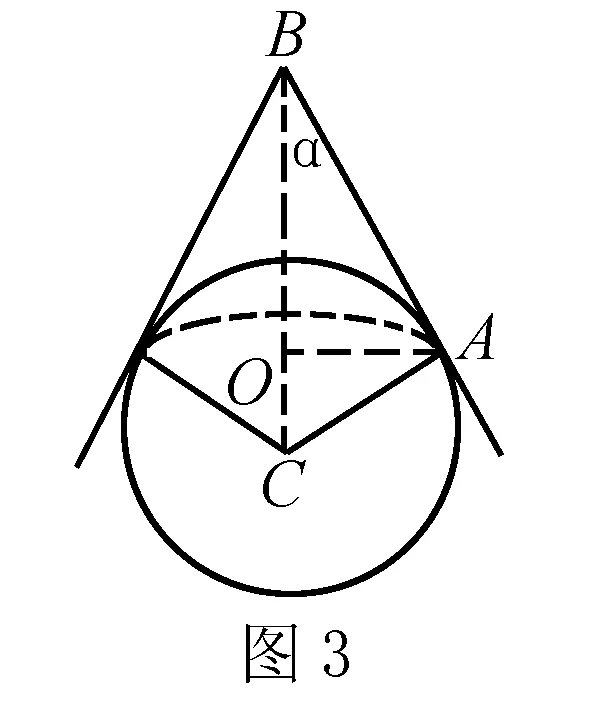

分析2 在球體上,假設有一個圓錐體相切于繩套處,如圖3. 則問題轉化為例1中的圓錐體上繩套的張力問題,就可用例1的結果.
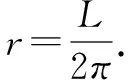
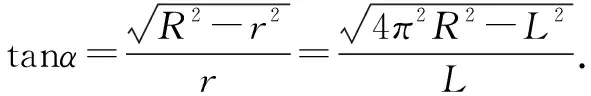
所以利用例1的結果就得到所求的繩子的張力為
三、將圓錐體推廣為更一般的旋轉體
例3 如圖4,一質量為m的均勻閉合細繩套在一光滑的花瓶上,花瓶表面是一個旋轉體的表面. 旋轉體表面是由函數y=1-x2繞著y軸旋轉一周得到的,繩套的長度為L. 求解當細繩平衡時,繩中的張力為多少?
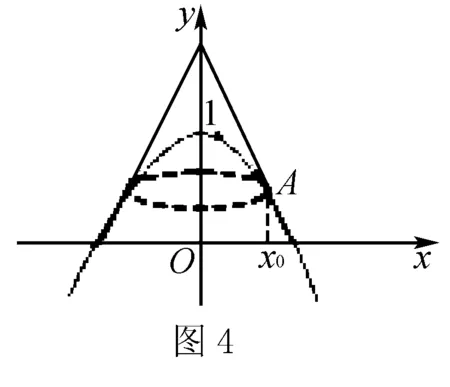
分析在這個花瓶上,也同樣假設有一個圓錐體相切于繩套處,如圖4. 則問題轉化為例1中的圓錐體上繩套的張力問題.
解(轉化法) 假設有一個圓錐體相切于繩套處,如圖4. 那么鐵球體上繩套中的張力就變為圓錐體上的繩套的張力問題. 所以只需要求出相切的圓錐體的半頂角α即可.
所以利用例1的結果就得到所求的繩子的張力為

最后再留一個問題,對于更一般形狀的,比如光滑的橢球體,是否有解決辦法?

