“導數的綜合應用”的教學設計與反思
陳 琦
(江蘇省啟東中學 226200)
一、教材分析
導數的綜合應用”是高中數學蘇教版教材選修2-2第一章的內容,它是中學數學與大學數學的一個銜接點.導數的應用為我們解決所學過的有關函數問題提供了一般性方法,是解決實際問題強有力的工具 ,它是高考考查的重點和難點,題型既有靈活多變的填空題,又有具有一定能力要求的解答題,這要求我們要掌握基本題型的解法,樹立利用導數處理問題的意識.
二、教學目標分析
1.知識與技能目標
能利用導數解決與切線有關問題,會求函數的單調區間、極值、最值,解決含參方程的零點、含參不等式恒成立等問題.
2.過程與方法目標
能利用函數性質作圖象,反過來利用函數的圖象研究函數的性質,如交點情況,能合理利用數形結合解題;學會利用轉化思想將陌生的問題轉變為熟悉問題,提高發現問題、分析問題、解決問題的能力.
3.情感、態度與價值觀目標
這是一堂習題課,教學難度有所增加,培養學生思考問題的習慣,以及克服困難的信心.
三、教學重點與難點
教學重點:熟練函數的單調區間、極值、最值的求法,導數幾何意義的應用.
教學難點:函數零點個數和不等式恒成立問題的轉化.
四、教學過程
1. 溫故·習新
問題(1)導數的應用有哪些?
(2)已知函數f(x)的導函數f′(x)=3x2+8x+4的圖象如下,請作出原函數f(x)的圖象.

【師生互動】師拋出問題(1),學生口答單調性、極值、最值、實際問題.接下來師給出問題(2)的圖象(圖(1)),請一個學生在黑板上作出草圖(圖(2)),其實圖(2)作得不對,是一系列曲線族,其余同學在草稿紙上畫圖,并分析畫圖思路,鞏固理解函數單調性和導數的關系.
【設計意圖】由問題帶動學生對知識的回憶,既回顧知識又調動了學生參與課堂的積極性,通過學生動手作圖的過程進行知識和信息的整理,為后面的例題做鋪墊,起到了事半功倍的作用.
2.釋疑·拓展
例1 已知函數f(x)=x3+4x2+bx+c.
(1)若b=0時,則函數的單調增區間是____; 函數的極小值是____極大值是____; 函數在區間]-3,0]上的最大值是____.(2)若點P(-1,3)是函數圖象上的點,在點P處的切線斜率是-1,求b,c.
【師生互動】學生課前獨立完成,師投影儀顯示生的解答,并請生講解;對于問題(2)師做拓展延伸:將(2)中的“在”改為“過”呢?
【設計意圖】鞏固學生對導數在單調性、極值、最值上的簡單應用.做適當的復習延伸是為了讓學生更加明確導數的幾何意義與曲線的切線之間的關系,特別是區分“在一點”與“過一點”注意細節,避免混淆.
例2 已知函數f(x)=(a+1)lnx+ax2+1.
(1)討論函數f(x)的單調性;(2)設a≤-2,如果對任意x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范圍.
【師生互動】對于(1)師引導學生求導后變形,對參數a進行討論,對于(2)先讓學生分組討論,重點分析如何等價變形去絕對值,構造函數利用單調性解決問題,并詳細板書.生完成并矯正.
【設計意圖】設計了一道高考題,旨在讓學生重視導數的綜合應用,同時也讓學生的探究熱情達到高潮.這道題,運用了分類討論和構造函數的思想,這也是高考的熱點.
3.反饋·提煉
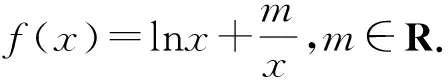
【師生互動】學生自主完成師的精選題目,師在學生做題的時候,巡視生可能出現的問題,并且當堂批改矯正.
引導學生總結,師進行補充:本節課我們主要學習了導數的應用,設計單調性、極值、最值、恒成立問題及構造函數證明不等式,通過本節課的學習,可以加強合理應用數形結合,分類討論,構造函數的思想.
【設計意圖】從常規教學模式的宗旨出發,設計與典型例題相關的反饋練習,起到及時捕捉學生的動態和復習后的疑問作用.讓學生自己小結,不僅僅總結知識更重要地是總結數學思想方法.這是一個重組知識的過程,這樣可以幫助學生自行構建知識體系,理清知識脈絡,養成良好的學習習慣.
四、教學反思
這堂課,通過挖掘和呈現更好促進學生積極主動地進行數學思考,使學生主動地投入到課堂中來,逐步學會判斷和探索,進一步提高數學思維的能力和水平.并在合作討論中發現并表現自我,增強他們的團隊合作意識,讓學生終生受益.“根深之樹不人風折,泉深之水不會涸竭”,只要讓學生在平時的學習中夯實基礎,提升思維,相信在以后的高考中定能不亂不燥,取得較好的成績.而學習數學知識中所養成的良好品質對學生將來的生活和工作將會產生更加深遠的影響.

