例談教學中如何進行深入思考
顧 婷
(江蘇省無錫市玉祁高級中學 214183)
眾所周知,高中數學科對于高中學生而言是學習最為困難的學科,造成困難的原因是多樣的,其中不乏數學知識的形式化、抽象性,數學解題技巧的層出不窮,數學問題的變化多端、無固定性,數學理解的困難等等.大量調查資料也顯示,大多數學生在數學學習過程中,出現下意識操作、直覺化操作,對于問題的深入思考幾乎是零,這與學生長期受制于灌輸式教學不無關系.
可以這么說,現階段難度在學考水平的數學問題,幾乎是下意識操作,有部分問題是一個“彎角”;難度在高考層面的數學問題,一部分是下意識操作,一部分是一個“彎角”,一部分是兩個“彎角”,因此學生在學習過程中若一貫的缺乏主動、深入的思考,導致最終就不善于思考,從而形成了學習的停滯不前.
一、概念教學中的深入思考
概念教學是數學教學的核心和重中之重,人民教育出版社主編北師大錢佩玲教授對于當下的中學數學概念教學是有異議的,認為當下的數學教學根本是功利性的教學,完全脫離了編者的初衷,各種教輔資料也是魚龍混雜,對概念的考查和理解偏頗較大,一方面因為應試需要所以草草了事,一方面因為教學不扎實導致學生不會解決問題,又反復教學.錢教授所說的這種行為,至少在中學數學常態課教學中并非個例.以筆者來看,我們的概念教學的確是出了問題,教學中缺乏對概念設計的深入思考,導致概念教學只能一個定義、三項注意,從而形成了以做題替代概念的理解方式.
案例1 《正余弦定理》概念教學
眾所周知,正余弦定理是解三角形中的重要知識,除了最基本的兩個定理之外,可以這么說,學生對正余弦定理的理解幾乎是零.筆者曾經調查過學生:正余弦定理怎么得到的?正余弦定理跟初中數學什么知識密切相關?正余弦定理如何在不用具體運算的角度下,就可以判斷三角形解的個數?令人驚訝的是,90%以上的學生一個問題都不知道,三個問題都能回答清楚的學生人數是零.這不得不說是我們概念教學的悲哀,給學生一個三角形的問題,他可以解得頭頭是道,但是一問原理則是一片模糊,這不正是應試教育的產物,時代的悲哀?
試問,老師自己有沒有思考過這樣的問題:正余弦定理跟初中數學什么知識密切相關?正余弦定理如何在不用具體運算的角度下,就可以判斷三角形解的個數?讓我們自己先來一番深入的思考吧:初中數學對于全等三角形的判斷主要依賴三種方式:SSS、SAS和AAS,但是SSA不是全等的判別條件.對于這些熟悉的判別方式,我們有沒有思考過和正余弦定理有什么聯系嗎?余弦定理知道三邊可以求解唯一三角形,余弦定理知道兩邊一夾角可以唯一求解其余所有量,正弦定理利用兩角一對邊可以求解唯一求解其余所有量等等.所以,我們有了下面的初高中知識的連接:
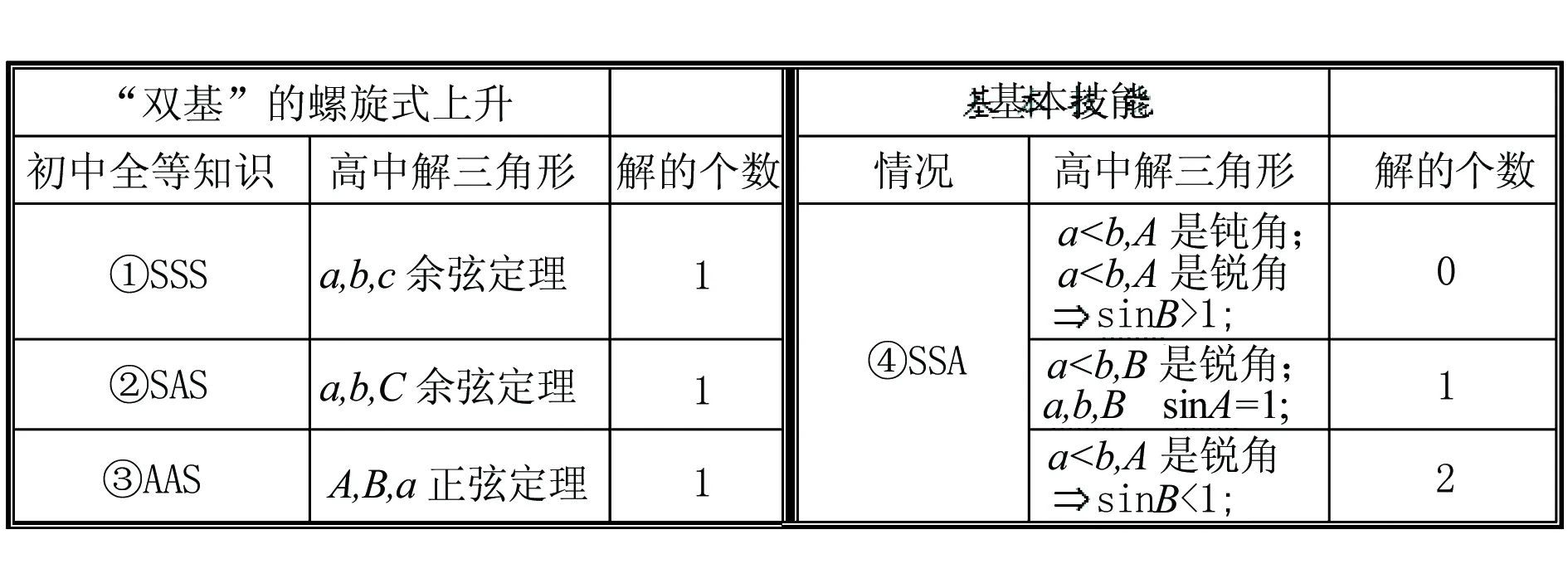
給出具體問題:在△ABC中,由下列各組條件求解三角形,其中有兩個解的是____.
①b=20,A=45°,C=80°;
②a=30,c=28,B=60°;
③a=14,b=16,A=45°;
④a=12,c=15,A=120°;
⑤a=4,b=5,c=6;
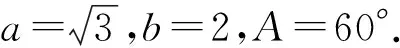
分析有了上述的深入思考,將三角形解的判斷與全等三角形知識聯系起來,從初中定性的判定,到高中定量的運算,其中之間的聯系,進行了深入的思考,從而理解了為什么有一解,為什么有兩解.簡解如下:第①項,AAS,必定一解;第②項,SAS,必定一解;第③項,SSA,sinB<1且a
說明:從三角形解的個數判斷的角度來說,實在是全等三角形的判定,初中數學強調的是定性,高中數學更追求的是定量,這一層面若能思考到位,自然將初中數學和高中數學這一知識點銜接起來,獲得了更多的教學思考,學生也能獲得更多的知識理解,明白了正余弦定理各自對待的不同情況,對知識的深入思考有助于思維的嚴密性和嶄新認識.
二、解題教學中的深入思考
數學問題以抽象性著稱,問題的求解過程實質是不斷轉化、不斷深化思維的過程,從解題教學來看,如何讓學生掌握問題解決過程中思維的實質是關鍵.筆者以為,這需要探析教學中思考的重要性,以恒成立問題為例,如何引導學生理解恒成立問題解決的原理?如何破解成為關鍵.

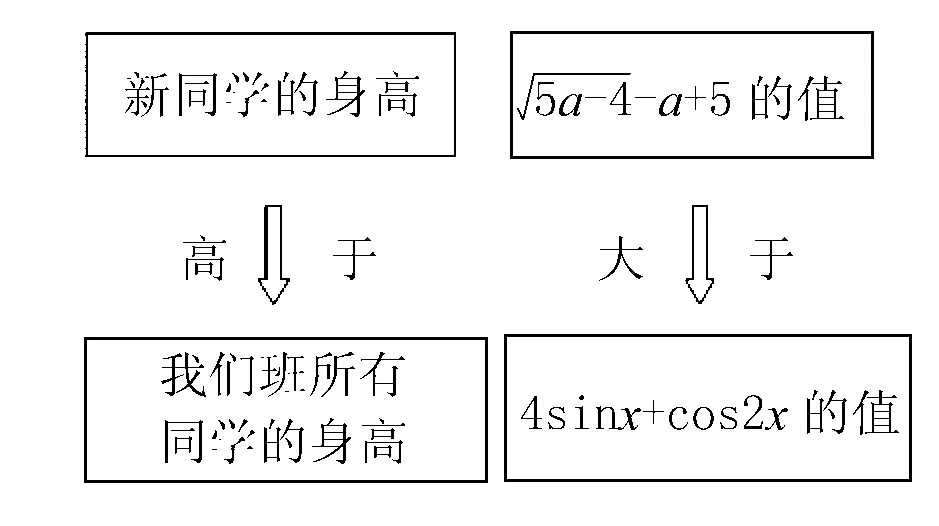
分析本題是單變量恒成立問題,變量是x,參量是y,從這其中尋找恒成立問題解決的一般原理.要思考如何將這個原理表述的更為貼切?讓學生易懂?筆者給出了這樣的比喻:
教師設喻:(如圖)若我們班即將來一位新同學,目前我們只知道他比我們班任何一個都要高,那么你們能否猜出他的身高范圍?
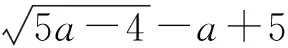
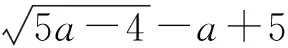

學生試著設喻:(如圖)學校搞活動,從體育學校來了一個籃球班,所有人的身高都高于我們班同學.
說明:恒成立問題需要說明參變分離做法的合理性,這就需要教師深入的思考,為什么要參變?為什么大于最大值?小于最小值?這些問題解決理論研究清楚了,自然而然獲得了最為合理的本質探究.教師要做到,恰恰是對數學最深入的思考,唯有自身努力的思考,才能讓學生更為深刻地理解數學本質,這正是思考的價值所在.
總之,教學不能僅僅只教會表層的解題使用,更要注重數學知識的理解,從核心素養的角度來說,教學更要從根本入手,更要關注思考的價值,久而久之才能培養學生的思維,使其真正理解數學、運用數學,對于教師而言也能獲得更多的專業化成長.

