淺議構造法在初中數學解題中的有效運用

李 斐

(江蘇省泰興市新街初級中學 225474)

一、重視題意分析

分析題意是大多初中學生所必須要掌握的一項內容，也只有弄清題目的具體意思，并據此找到已知條件、未知條件、隱含條件等，才能理清條件與問題之間的關系，并盡快找到問題的切入點以及解題的具體思路.在采取構造法引導學生進行解題的過程中，教師應重點關注學生對題意的分析與理解情況，并據此判斷學生在邏輯分析與題意分析方面存在的問題，并有針對性地調整教學策略，以此不斷提高學生的數學解題能力，提高學生的解題效率.

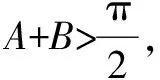
二、找到解題思路

在傳統的解題教學當中，大多數教師在解題教學過程中主要是直接給出具體的解題思路，并未意識到學生需要鍛煉與培養，如若教師長期給出具體的解題思路，學生必然會產生依賴性，導致其解題能力、題目分析能力一直得不到有效的提高，這對于其今后的學習與發展毫無益處.因此，教師在考慮教學進度的同時必須要重點培養學生的獨立解題能力，讓其能在解題過程中積極運用所學知識以及題目的有限條件找到解題的思路，讓學生的解題能力在不斷的鍛煉中得到有效的提高.

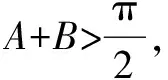
三、重視歸納總結

對于大多數學生而言，數學本身就是一門相對較為難學的課程，沒有語文、英語等人文學科那般隨心所欲，學生需要根據既定公式、推理模式等進行解題，而且問題最終的答案大多具有唯一性.在新的時代背景下，傳統的解題教學模式已經無法適應現代學生的學習要求，教師必須要及時對教學模式進行完善與創新，在豐富學生體驗、提高學生興趣的基礎上夯實其解題能力.值得注意的是，構造法既然在初中數學解題教學中具有如此之高的運用價值，教師則必須要充分發揮此種方法的作用與價值，并引導學生做好相應的總結與歸納工作，從而幫助其及時理清知識脈絡、完善知識系統，最終促進學生學習與解題能力的不斷提高.仍然以上面所提到的題目為例，這個例題涉及到了學生較為陌生的三角函數，為了幫助其盡快找到解決問題的思路、掌握相關的數學知識，并構建良好的知識系統，教師則必須要引導學生對解題過程進行歸納與總結，A學生在解題的過程中運用到了正玄定理與余弦定理，教師可以引導其歸納總結正余弦定理的運用過程與運用方式；B學生的解題思路側重于函數知識的運用，教師則可以引導其歸納總結與函數相關的知識，并讓學生在學習之余多回顧、復習總結的知識與內容，從而在今后解題過程中能迅速從腦海中提取出相應的知識進行解題.除此之外，在有條件的情況下，教師還可以組織學生進行交流分析，讓其分享一下總結歸納的具體內容，并通過知識共享的方式來搭建完善的數學知識網絡，最終實現合作共贏，從而不斷提高其數學學習效果與解題能力.

總而言之，在新的時代背景下，傳統的數學教學模式已經無法滿足學生們的學習與探究需求，教師在對教學模式進行改革與完善的同時，還應當將構造法納入數學解題教學過程中，讓學生在解題的過程中能做到認真分析與解讀題意，并找到多種不同的解題思路，從而盡快求出問題的答案.在這個過程中，學生的解題能力、邏輯思維能力以及知識構造能力均得到了良好的鍛煉.除此之外，教師還應重點引導學生歸納與總結解題思路、過程，雖然數學問題千變萬化，但終究不離其宗，學生掌握具體解題思路與方法之后，數學知識結構自然建立起來，解題效率也會得到相應的提高.